2. Расчетно-графическая работа №2 «Получение эллипсов погрешностей для оценки точности хода полигонометрии».

Цель: Получить элементы абсолютных и относительных доверительных эллипсов погрешностей для каждой точки полигонометрического хода и изобразить их на схеме хода в произвольно выбранном масштабе.

2.1. Теоретические основы графического оценивания качества сетей

Для геодезиста, как и любого другого профессионала, важно уметь оценить и управлять качеством своей работы. Причины этого достаточно очевидны:

– работа должна отвечать определенным требованиям и таким образом мы должны быть в состоянии оценить, отвечают ли она этим требованиям;

– когда для некоторых случаев (плохая конструкция сети, большая погрешность наблюдения и др.) работа требованиям не отвечает, должны быть доступны некоторые инструменты для улучшения ситуации.

Контроль качества стал достаточно важным в последние годы в связи с развитием при геодезических работах инструментальной базы. Современные тотальные станции TPS и спутниковые приемники GNSS способны производить большие массивы геодезических данных, требуя, таким образом, более эффективные инструменты для оценивания их достоверности и точности.

Качество (точность) результата геодезического измерения определяется понятием средней квадратической погрешности (СКП, среднее квадратическое отклонение, англ. standard deviation std, стандартное отклонение) измерения. Эта величина выражает стохастическую изменчивость результата измерения. Точность сети может быть определена как влияние совокупности средних квадратических погрешностей измерений на результаты определения в сети координат точек в результате уравнивания.

Совокупность точностных характеристик полнее и лучше всего выражается ковариационной матрицей результатов измерений, или их функций.

При этом ковариационная матрица может быть задана в разных видах: собственно ковариационной матрицей классического представления; в виде корреляционной матрицы процесса и вектора, характеризующего меру рассеивания результатов; в виде матрицы кофакторов (обратной матрицы весов) и погрешности единицы веса (дисперсии единицы веса, дисперсионного фактора, англ. variance factor).

Связь между этими величинами можно представить в виде

. (1)

Здесь K, Q, P и R – ковариационная матрица, матрица кофакторов, весов и корреляционная матрица соответственно; – дисперсионный фактор (дисперсия единицы веса), М – диагональная матрица измерений, у которой по диагонали размещены средние квадратические погрешности измерений (оценки стандартов измерений).

Рассмотренные выше оценки носят название точечных оценок. Наряду с точечными оценками большое применение имеют интервальные оценки, при которых оцениваемая величина находится в какой либо доверительной области (интервал, фигура) с вероятностью . Отметим, что качество интервального оценивания гарантируется только при гауссовском распределении результатов измерений и резко падает при отклонении от него. Основа интервального оценивания качества объектов размерности больше 2 являются доверительные эллипсы (гиперэллипсоиды).

Доверительные эллипсы. Установление вида доверительной фигуры при интервальном оценивании двухмерных объектов (например, точек хода полигонометрии) производится на основе формулы плотности двухмерного нормального закона распределения измерений

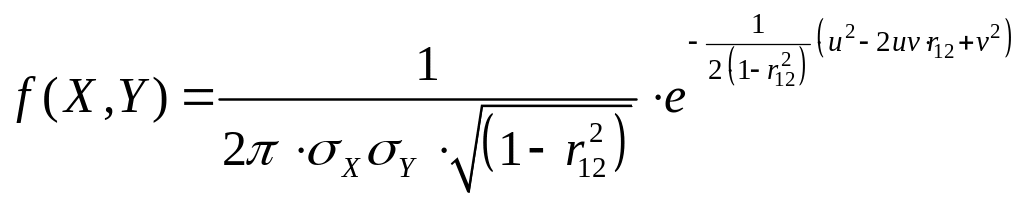(2)

Здесь

.

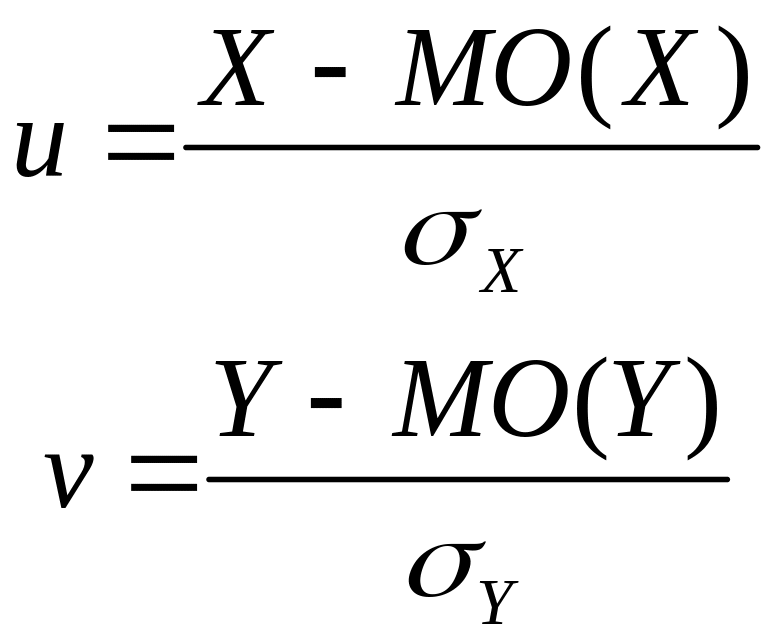две стандартизованные величины, r₁₂ – коэффициент корреляции между величиной X и Y. В сечении плоскостями, параллельными плоскости X0Y, графика для (2) будем иметь фигуры, которые при фиксированной правой части представляет собой эллипс с формулой

. (2)

Очевидно, что величина k в (2) связана с высотой сечения и т.о. с уровнем вероятности, которая постоянна на всем сечении. Поэтому эллипсы такого рода называют эллипсами равной плотности или эллипсами рассеивания. Для независимых величин уравнение эллипса рассеивания будет

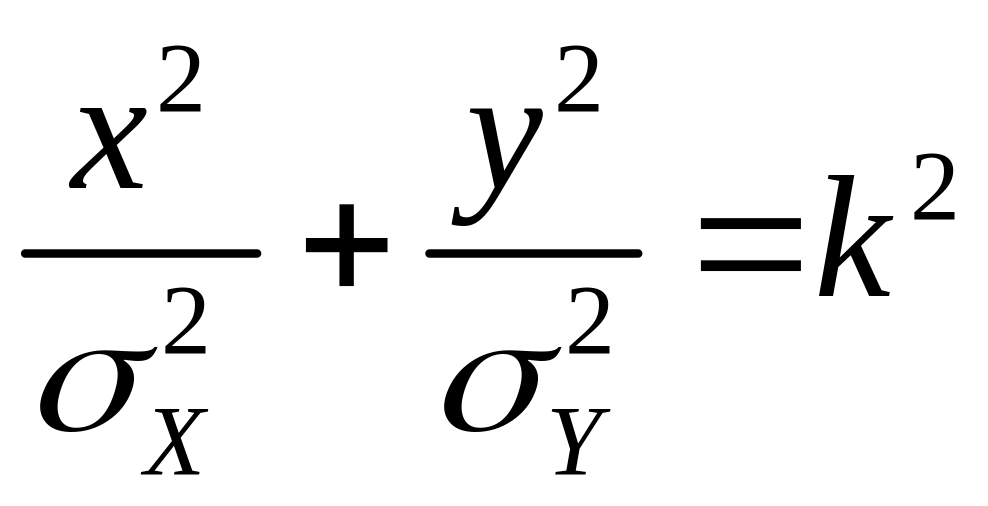(3)

или

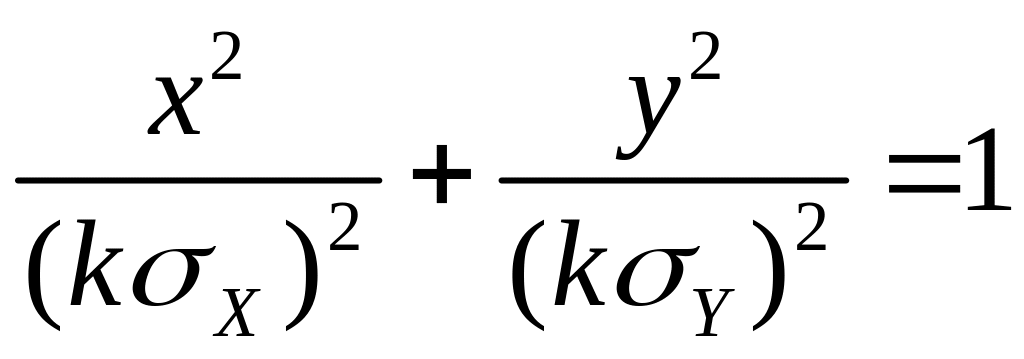. (3а)

Здесь k – постоянный коэффициент пропорциональности между полуосями эллипса и стандартами. Если полуоси равны стандартам, т.е. k = 1, то такой эллипс называют единичным (стандартным, средне-квадратичным) эллипсом рассеивания.

Вероятность попадания случайной точки в эллипс рассеивания, полуоси которого равны k стандартам есть

. (4)

Из формулы (4) величина k при заданной вероятности будет

. (5)

Например, для единичного (стандартного) эллипса рассеивания с полуосями и k = 1 имеем .

Теперь, чтобы получить размеры эллипса, вероятность попадания точки в который равна , по формуле (5) вычисляем нужный коэффициент k, на который домножаем значения вычисленных значений полуосей эллипса.

Например, если доверительная вероятность  = 0.95, то оси эллипса согласно (3а) надо умножить на k = 2.45.

Для трехмерного доверительного эллипсоида вероятность попадания случайной величины в него может быть получена как

. (6)

Например, для стандартного эллипсоида рассеивания с полуосями и k = 1 имеем .

Эллипсы для представления точности носят название средних квадратических эллипсов (доверительные эллипсы, эллипсы погрешностей). Средние квадратические эллипсы могут быть расценены как 2-мерный эквивалент средних квадратических отклонений. Для целей оценки точности выделяют абсолютные и относительные средние квадратические эллипсы.

Абсолютные средние квадратические эллипсы представляют собой распространение случайных погрешностей измерений через математическую модель уравнивания в определяемые координаты и показывают область рассеивания в определении положения точки относительно исходных пунктов. Ориентация абсолютного среднего квадратического эллипса определена углом  между большой полуосью эллипса и северной осью (осью Х) системы координат.

Относительные средние квадратические эллипсы представляют область рассеивания в определении положения одной точки относительно другой определяемой, или относительную точность между парами точек. Форма эллипса также определяется большой полуосью a и малой полуосью b. Ориентация относительного среднего квадратического эллипса определяется углом  между большой полуосью эллипса и соединительной линией между начальной и конечной точкой оцениваемой линии.

Основной способ получения элементов для определения эллипсов погрешностей из элементов ковариационной матрицы. Эллипсы обеспечивают графическое средство анализа качества результатов уравнивания сети и могут показать:

– Слабость ориентации (малые полуоси указывают на исходные даты);

– Слабость масштаба (большие полуоси, указывающие на исходные даты);

Также следует иметь ввиду, что абсолютные эллипсы погрешностей показывают эффекты исходных дат: например, у определяемых точек, которые дальше от исходных точек в сети, в общем эллипсы погрешностей имеют большие размеры, чем у точек, которые ближе к исходным точкам, а относительные эллипсы погрешностей не зависят от выбора исходных дат.

Построение эллипса погрешностей. Для построения плоского эллипса погрешностей используем комбинацию двух основных способов (вращений и собственных значений) как наиболее оптимального.

В качестве исходных данных используются блоки (K)_i размера (22) из общей ковариационной матрицы К для i-той точки, полученной после оценивания по методу наименьших квадратов

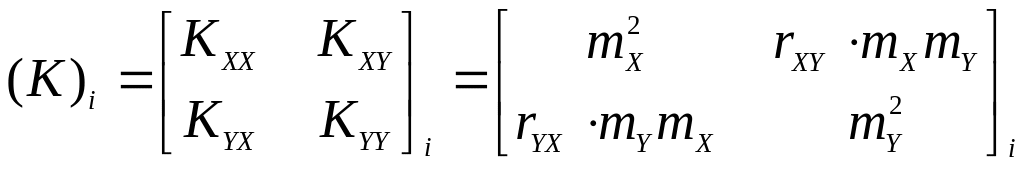(7)

При построении эллипса погрешностей способом вращений мы начинаем с блока ковариационной матрицы (25) для i-той точки, который определен в какой либо исходной системе координат [x, y]. Очевидно, что есть другая система координат [u, v], которую мы можем получить, вращая исходную систему [x, y] на некоторый угол  следующим образом:

(26)

Учитывая, что ковариационная матрица точки в системе координат [x, y] есть формула (25), новая система из (26) линейно связана со старой, соответствующая ковариационная матрица для точки в системе [u, v] может быть получена на основе теоремы переноса погрешностей (англ. law propagation of variance) как

(27)

Здесь – матрица линейного преобразования из (26).

Так как нас действительно интересуют только диагональные элементы ковариационной матрицы K(uv), т.е. элементы то выразим их явно на основе (27):

(28)

или

(28а)

Если задать угол  и произвести расчеты по (28а), то мы получим средние квадратические погрешности по осям, но в направлении, определенном углом .

Если по уравнениям (28а) просчитать все значения для углов 0   < 360, то будет получена упомянутая ранее педальная кривая, т.е. кривая, описывающая в любом направлении среднюю квадратическую погрешность определения пункта. Очевидно, нас интересует угол , в направлении которого величина соответствующей погрешности из (28а) будет максимальной, т.е. направление полуосей эллипса. Для этого возьмем например первое уравнение (28а) и получим по нему направление, в котором погрешность будет максимальна. Это можно произвести взяв производную от уравнения по , приравнять её значение к нолю и решить полученное выражение относительно угла :

Откуда

. (29)

Учитывая связь элементов ковариационной матрицы и матрицы кофакторов блока (29) можно записать как

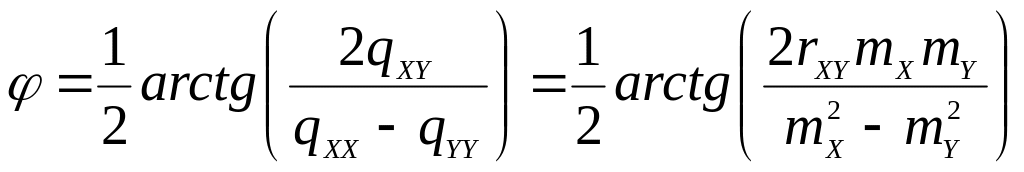. (29а)

Формулы (29) и (29а) имеет 2 решения с разворотом на 90 и таким образом задают направления большой и малой оси эллипса, но выдают значения со знаком в пределах от 0 до 90. Так как угол  аналогичен ориентирному направлению относительно вертикальной оси Х большой полуоси и может изменяться от 0 до 360, то для его идентификации целесообразно воспользоваться следующей схемой, аналогичной переводу румбов в дирекционные углы при решении обратной геодезической задачи по знакам числителя и знаменателя

Не сложно заметить, что если значение угла больше нуля, то его откладывают от вертикали по часовой стрелке, а если меньше нуля (не зависимо от числителя ли, или от знаменателя), то его откладывают от вертикали против часовой стрелки.

Используя полученное значение угла  из (29а) и подставив его в формулы (28а) получим значения большой и малой полуоси эллипса погрешностей в виде величин .

Получение элементов эллипса на основе собственных значений и собственных векторов. Можно показать, что квадратный корень из собственных значений ковариационной матрицы К соответствует длинам полуосей эллипса погрешностей, а собственные вектора, соответствующие этим собственным значениям, определяют направления полуосей эллипса погрешностей. Тогда для решения задачи используют известную в линейной алгебре формулу нахождения собственных значений матрицы:

det(K – E) = 0, (30)

или

. (30а)

Откуда

. (31)

Уравнение (31) имеет 2 решения вида

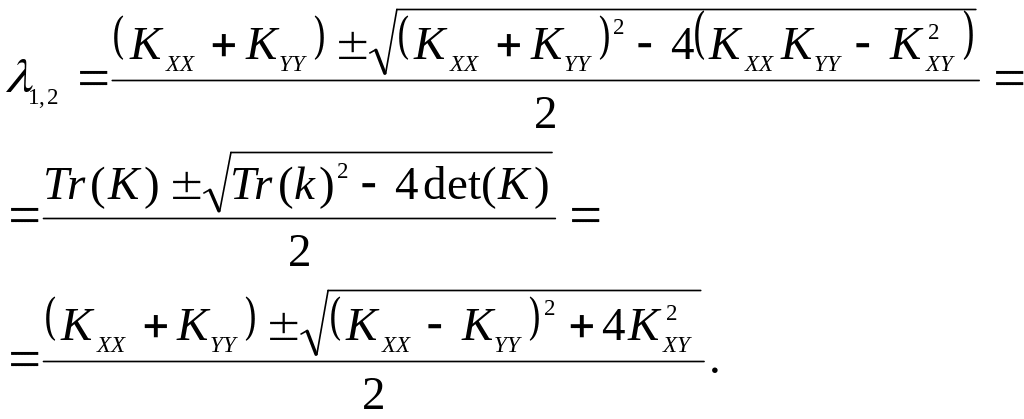(32)

Длины полуосей для стандартного эллипса погрешностей будут соответственно равны корню квадратному из собственных значений

. (33)

Соответствующие собственным значениям 1,2 собственные вектора (x1,y1) и (x2, y2) тогда можно получить из нетривиальных решений системы

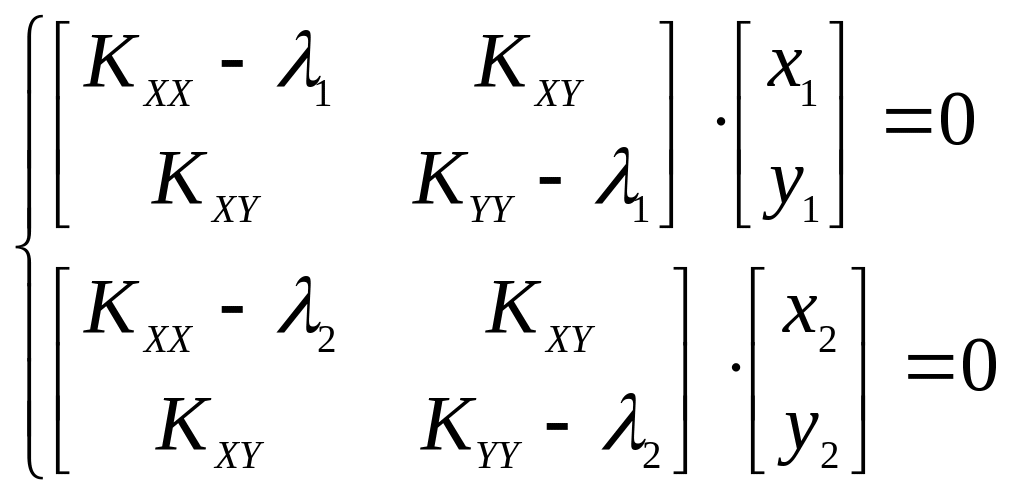. (34)

Эти собственные вектора определяют направление осей эллипса погрешностей и должны быть ортогональны друг другу. Решение не сложное, но не удобное, и поэтому в таком виде используется достаточно редко. На практике чаще всего используются комбинации 1 и 2 способов, получая ориентировку по (29), а длины полуосей по (32) и (33).

Алгоритм на основе собственных значений может использоваться, чтобы получить также трехмерный эллипсоид погрешностей для точки.

Если для геодезических целей требуется получить погрешность в направлении  (мостовая триангуляция, ориентировка туннелей, шахт и т.д. где это достаточно важно), то используют первые формулы в (28) и (28а). При использовании первых формул угол  является дирекционным углом (азимутом) оцениваемого направления.

Например, для получения погрешности в направлении  = 30 относительно северного исходного направления для точки i с блоком ковариационной матрицы по (28) имеем

Относительные эллипсы погрешностей. Относительный эллипс погрешностей представляет доверительную область при оценивании точности позиционирования i-той точки в сети относительно другой определяемой, j-той. Относительный эллипс погрешностей также получают из ковариационной матрицы, но используют блоки для Кi и Кj точки. Относительные эллипсы погрешностей рисуются на середине линии, соединяющей i-тую и j-тую точки, для которых представляется эллипс.

Чтобы построить относительный эллипс погрешностей между i-той и j-той точками, точность которых представлена общей ковариационной матрицей К, из неё извлекают диагональные блоки Кi и Кj и не диагональные Кij и Кji соответствующие нужным нам точкам. Из блоков формируем новую матрицу размера (4  4) вида

, (35)

для плановой (2D) сети. Далее строят вектор разностей координат по правилу, если точки идут в последовательности i  j, то в разности от координат конечной точки j вычитают координаты начальной точки i и формируют матрицу F из коэффициентов при координатах, используя таблицу:

	Xi	Yi	Xj	Yj
Xj – Xi	– 1	0	1	0
Yj – Yi	0	– 1	0	1

Как видим нужная для построения относительного эллипса матрица имеет размер (2  4) и состоит только из блоков единичной матрицы E

. (36)

Теперь используя закон переноса погрешностей K = FKijF^T из (35) и (36) имеем

, (37)

исходя из симметричности недиагональных блоков. Размер выходной матрицы 2  2. Далее, используя любой из описанных выше алгоритмов для расчета элементов эллипса, производят вычисление ориентировки и значений полуосей относительного эллипса.