1.3 Формы представления чисел в эвм

Формы, диапазон и точность представления чисел

Как известно, в ЭВМ применяется двоичная система счисления. Может быть доказано, что при этом на построение ЭВМ тратится наименьшее количество базовых аппаратных элементов — «венти­лей». Точнее, оптимальным основанием системы счисления по кри­терию «минимум аппаратных расходов» является основание нату­рального логарифма е= 2,72.

Однако по ряду очевидных причин для ЭВМ принято Р=2. Достаточно вспомнить, что одна из первых электронных ВМ ENIAC содержала 17 468 электронных ламп, имела размеры около 6 м в высоту и 30 м в длину. Обилие применяемых вакуумных ламп, габаритные размеры машины отчасти объяснялись тем, что она ра­ботала с десятичными числами.

Двоичные числа в компьютерах размещаются в ячейках памяти или в регистрах, которые состоят из запоминающих элементов — триггеров.

В ячейке или триггере хранится значение одного двоичного разряда — бит информации.

Разрядной сет­кой компьютера называется совокупность запоминающих элементов для размеще­ния одного двоичного числа. Для разных классов компьютеров длина разрядной сетки составляет 8, 16, 32, 64 и больше разрядов.

Форматом называется способ размещения компонентов числа в разрядной сетке, то есть последовательность и позиции знака, мантиссы, порядка и др.

Формы представления чисел

В компьютерах используются две формы представления числа:

• с фиксированной запятой перед старшим разрядом числа (для правильной дроби) или после младшего (для целого числа);

• с плавающей запятой, место положения которой задается порядком числа.

Место запятой в обоих форматах понимается неявно, без использования до­полнительных разрядов. По традиции нумерация разрядов в больших машинах осуществляется слева направо, а в мини- и микрокомпьютерах и микропроцессорах— справа налево.

Фиксированная запятая (точка).

З амечание. В русском языке принято называть разделитель целой и дробной части дроби запятой, а в английском – точкой. Поскольку современная вычислительная терминология формировалась на английском языке, то словосочетания «фиксированная точка» и «плавающая точка» вошли в русскую компьютерную лексику.

В форме представления с фикси­рованной запятой (точкой) числа изображаются в виде последова­тельности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например, для числа 1355,1875₍₁₀₎, что соответствует 010101001011,0011₍₂₎, запись следующая:

Целая часть Дробная часть

010101001011

0011

=1355 + 3/16

15 4 3 0

Представление числа с фиксированной точкой концептуально самое простое, берется двоичное число и объявляется, что определенная часть его младших разрядов представляет собой дробную часть в позиционной системе счисления.

Например, пусть числа представлены в десятичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять в дробной части (после запятой).

Числа, записанные в такую разрядную сетку, имеют вид:

+00721.35500.

+00000.00328.

-10301.20260.

Диапазон значащих чисел N в системе счисления с основанием Р при наличии т разрядов в целой части и s разрядов в дробной части числа (без учета знака числа) будет таким:

P^-s ≤ N≤ P^m – Р^-s

Например, при Р=2, m=10 и s = 6 числа изменяются в диапазо­не 0,015 < N< 1024. Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение раз­рядной сетки, и дальнейшие вычисления теряют смысл.

Положение запятой строго фиксировано и при этом предполагается:

- положение запятой закрепляется в определенном месте и сохраняется неизменным для всех чисел, изображаемых в принятой разрядной сетке машины;

- хотя запятая и фиксируется, но никак не выделяется в коде числа, а только подразумевается.

Обычно в ЭВМ используется два способа расположения запятой:

-перед старшим разрядом (Р=0);

-после младшего разряда (Р=n), где n –число разрядов, отводимых под цифровую часть числа. Во втором случае представляются только целые числа со знаком.

Выход исходных чисел, а также чисел, полученных в процессе вычислений, за пределы допустимого диапазона приведет к грубым ошибкам. Чтобы этого избежать, необходимо при разработке программ исходные числа масштабировать.

Недостатки. Имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях. В современных компьютерах естественная форма представления использу­ется как вспомогательная и только для целых чисел.

Достоинство. Эта форма наиболее проста, естественна и для представления чисел с фиксированной точкой можно построить сравнительно несложное арифметическое устройство с высоким быстродействием.

В памяти ЭВМ числа с фиксированной точкой хранятся в трех форматах:

а) полуслово — 16 бит, или 2 байта;

б) слово — 32 бита, или 4 байта;

в) двойное слово — 64 бита, или 8 байтов.

Отрицательные числа с ФТ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается за­меной единиц на нули, а нулей на единицы в прямом двоичном коде.

В числах со знаком выделяют дополнительный знаковый разряд (обычно, край­ний слева). В нем для знака плюс записывают цифру 0, а для знака минус — циф­ру 1. В числах без знака все разряды числа определяют модуль. Форматы двоичных дробных и целых чисел со знаком, с нумерацией разрядов справа налево и значением их веса показаны на рис. 1.7.

7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 Нумерация разрядов

+/-

26

25

24

23

22

21

20

+/-

,

2-1

2-2

2-3

2-3

2-4

2-6

2-7

Форма байта для целого числа Форма байта для правильной дроби

Рисунок 1.7 – Формат байта

Числа в разрядную сетку записывают в соответствии с весом позиций. Не заня­тые разряды заполняют нулями, как это показано на рис. 1.8 для чисел +0,725₁₀ = +0,10111₂ и -47₁₀ = -101111₂.

7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0

1

0

1

0

1

1

1

1

0

,

1

0

1

1

1

0

0

Запись целого числа -101111₂ Запись правильной дроби +0,10111₂

Рисунок 1.8 – Запись чисел

Интервал числовой оси, заключенный симметрично между максимальным и минимальным значением числа, называется диапазоном представления.

Абсо­лютное значение целого числа А изменяется в пределах:

А_min ≤ | А | ≤ А_max А_min = 1; А_max = 2^k - 1, (1.1 )

где к— количество разрядов цифровой части числа.

Из выражения (1.1) следует, что числа, по абсолютному значению меньше еди­ницы, воспринимаются как "машинный нуль"; числа, больше А_max, вызывают пере­полнение разрядной сетки. Диапазон представления целых чисел с учетом симмет­рии относительно нуля числовой оси

D

Пример 1.1

Рассчитать максимальное значение и диапазон представления целого числа со знаком в 16-разрядной сетке. На основе выражений (1.1) и (1.2) для k = 15 по­лучаем:

А_max = 2¹⁵ - 1 = 32767; D = 2А_max = 65534.

_A = 2A_max = 2(2^k-1) ≈ 2^k-1 (1.2)

Абсолютное значение правильной дроби В изменяется в пределах:

В_min ≤ | В | ≤ В_max В_min = 2^-k В_max = 1 - 2^k, (1.3)

Правильная дробь, по модулю меньше 2^-k, воспринимается как "машинный нуль"; числа, больше единицы, вызывают переполнение разрядной сетки.

Диапазон представления правильной дроби:

D

Пример 1.2

Рассчитать максимальное значение и диапазон представления правильной дроби в 16-разрядной сетке. На основе выражений (1.3) и (1.4) для k = 15 по­лучаем:

В_max = 1 - 2¹⁵ = -32767 D = 2В_max = -65534.

.

_B = 2B_пах = 2(1-2^-k) ≈ 2 (так как 1 >> 2^-k. ) (1.4)

Точность представления чисел в компьютере определяется абсолютной и от­носительной погрешностью.

Абсолютная погрешность ∆ представления чисел в ком­пьютере составляет:

для целых чисел: ∆А = 1/2 = 2^-1 где А –целое число (1.5)

для правильной дроби: ∆В = 2^k/2 = 2^-(k+1) где В –правильная дробь (1.6)

Из выражения (1.5) следует, что абсолютная погрешность представления це­лых чисел в форме с фиксированной запятой равна половине младшего разряда и не зависит от длины разрядной сетки. Из выражения (1.6) видно, что абсолютная погрешность представления правильной дроби в форме с фиксированной запятой уменьшается при увеличении длины разрядной сетки.

Относительная погрешность δ представления числа задается отношением аб­солютной погрешности к текущему значению числа и находится в пределах

δ_min ≤ δ ≤ δ_max

Для целых чисел в форме с фиксированной запятой минимальное и макси­мальное значения относительной погрешности

δ_Amin = = ≈ 2^-(k+1) δ_Amax = = = 0,5

Такими же формулами определяются минимальное и максимальное значения относительной погрешности для правильной дроби с фиксированной запятой.

Отно­сительная погрешность представления чисел в форме с фиксированной запятой существенно зависит от значения числа и значительно возрастает для малых чисел.

Числа с плавающей запятой

Вычислительные системы широко используют представление чисел с плавающей точкой. Идея этого представления состоит в том, чтобы нормализовать позиционную двоичную дробь, избавившись от незначащих старших нулевых битов освободив место для (возможно) значащих младших разрядов. Сдвиг, который нужен для нормализации, записывается в битовом поле, называемое порядком. Само же число называется мантиссой.

Пример. Число 0072.3500₍₁₀₎ -до нормализации и 0,7235х10² -после.

В двоичной СС запись будет следующей: до нормализации -001001000,100011 и после -1001000100011 х 2⁷

Целая часть Дробная часть

0

0

1

0

0

1

0

0

0

,

1

0

0

0

1

1

До нормализации

15 6 5 0

1

1

1

1

0

0

1

0

0

0

1

0

0

0

1

1

После нормализации

Порядок =7 мантисса

В форме представления с плаваю­щей запятой (точкой) число изображается в виде двух групп цифр:

• мантисса;

• порядок.

При этом абсолютная величина мантиссы должна быть мень­ше 1, а порядок должен быть целым числом.

Например, приведенные ранее числа в нормальной форме запи­шутся следующим образом:

+0,721355 х 10³;

+0,328 х 10^-3;

-0,103012026 х 10⁵.

Нормальная форма представления обеспечивает большой диапа­зон отображения чисел и является основной в современных компь­ютерах.

В форме с плавающей запятой числа представляются в виде произведений:

C = q^П ∙M = X∙ M (1.7)

г де q — основание системы счисления (обычно целая степень числа 2);

П — поря­док числа длиной k+1 (целое число со знаком, где к –число знач.цифр);

М— мантисса числа длиной г +1 (правильная дробь со знаком);

X - характеристика числа.

Знак всего числа опреде­ляется знаком мантиссы.

Для мини-компьютеров основания порядка и мантиссы совпадают (далее предполагается этот случай), а для больших машин — они раз­личны. Представление числа формулой (1.7) называют также полулогарифмиче­ским, потому что только часть числа — характеристика — представляется в лога­рифмической форме.

Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде.

Нормализованным называют такое число, старший разряд ман­тиссы которого больше нуля. У нормализованных двоичных чисел, следовательно, 0,5 < │М│< I.

Нормализованные, т. е. приведенные к правильной дроби, числа:

10,35₁₀ = 0,1035₁₀ x 10⁺²;

0,00007245₈ = 0,7245₈ х 8 ^-4;

F5C,9B₁₆ = 0,F5C9B₁₆ x 16⁺³;

В памяти ЭВМ числа с ПТ хранятся в двух форматах:

• слово — 32 бита, или 4 байта;

• двойное слово — 64 бита, или 8 байт.

Разрядная сетка для чисел с ПТ имеет следующую структуру:

• нулевой разряд — это знак числа (0 — «минус», 1 — «плюс»);

• с 1 по 7 разряд записывается порядок в прямом двоичном коде, пустые разряды заполняются нулями. В первом разряде указывается знак порядка (1 — «плюс» или 0 — «минус»);

• с 8 по 31 (63) указывается мантисса, слева направо без нуля целых в прямом двоичном коде и для отрицательных чисел и пустые разряды заполняются нулями.

Мантисса называется нормализованной, если ее значение определяется нера­венством вида

≤ |M| < 1 т.е. для основания q = 2 имеем: 0,5 < М< 1.

т

Пример 1.3

Иллюстрация записи числа с плавающей запятой: А₂ = 2¹∙110,111 = 2²∙11,0111 = 2⁴∙0,110111

о есть в старшем разряде модуля мантиссы должна быть записана единица.

Значение порядка (П = 1, 2 и 4) указывает на количество позиций, на которые "плавает" за­пятая.

Формат числа с плавающей запятой в 16-разрядной сетке показан на рис. 1.8. Тут для модулей порядка и мантиссы отведено соответственно пять (с 10 по 14) и девять (с 0 по 8) разрядов. Запятая в порядке размещена (условно) после младшего разряда, а в мантис­се — перед старшим. Знаки порядка и мантиссы размещены перед их старшими разрядами.

15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 Нумерация разрядов числа

+/-

Порядок

+/-

Мантисса

Рисунок 1.8 –Формат чисел в форме плавающей запятой

Абсолютное значение числа С в форме с плавающей запятой с учетом формул (1.7), (1.9) и (1.13) изменяется в пределах

X_min M_min = C_min ≤ |C| ≤ C_max = X_max M_max (1.8)

где X_min =2^-Пmax ( П_max = 2^r -1, где r –разрядность модуля порядка )

M_min =2^-1

X_max =2^+Пmax

M_max =1-2^-k (k –разрядность модуля мантиссы)

Диапазон представления чисел в форме с плавающей запятой

D

Пример 1.4

Рассчитать значение диапазона Д_C для числа С при г = 5, к = 9. С учетом выражения (1.15) получаем:

если П_max = 2^r -1= 2⁵ – 1 = 31 то D_C =2^+Пmax+1 =2³¹⁺¹= 2³²

что приблизительно соответствует десятичному числу 10^32∙0,3 ≈ 10⁹.

Диапазон представления чисел с плавающей запятой приблизительно больше в П_max раз диапазона представления чисел в форме с фиксированной запятой.

_C = 2C_max = 2∙ 2^+Пmax(1-2^-k) ≈2^+Пmax+1 (1.9)

Абсолютная погрешность представления чисел в форме с плавающей запятой зависит от погрешности мантиссы и порядка числа:

∆С = ∆М∙2^±П; ∆М =2^(k+1) (1.10)

где ∆M— погрешность представления мантиссы.

Минимальная и максимальная относительные погрешности представления чи­сел в форме с плавающей запятой не зависят от характеристики (она записывается в числителе и знаменателе выражения и потому сокращается).

С учетом формул (1.14) и (1.16) относительные погрешности рассчитывают из соотношений:

δC_min = = = 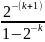2^-(k+1) ; δC_max = = = 2^-k (1.11)

Из выражений (1.17) следует, что относительные погрешности представления чисел в форме с плавающей запятой практически постоянны во всем диапазоне чи­сел.