Раздел 2. Случайные величины

Случайной величиной Х называется функция, определенная на пространстве элементарных событий Ω и принимающая числовые значения. Причем для любого действительного х определена вероятность

Р(Х<х) = F(x), (15)

которая называется функцией распределения случайной величины Х.

Функция распределения F(х) – неубывающая, непрерывная слева функция, определенная на всей числовой оси.

Свойства функции распределения:

1. 0 ≤ F(x) ≤ 1;

2. P(a ≤ X≤ b) = F(b) – F(a);

3. F(–∞) = 0, F(+∞) = 1.

Случайные величины бывают трех типов: дискретные, непрерывные и смешанные (дискретно-непрерывные).

Случайная величина называется дискретной, если она может принимать конечное или бесконечное счетное число значений.

Случайная величина называется непрерывной, если она может принимать бесконечное несчетное число значений (например, значения из какого-то интервала на числовой оси).

Если Х – дискретная случайная величина (ДСВ), принимающая значения х₁, х₂, … с вероятностями р₁, р₂, … соответственно, то ее функция распределения выражается формулой

(16)

Формулу (16) можно записать в виде

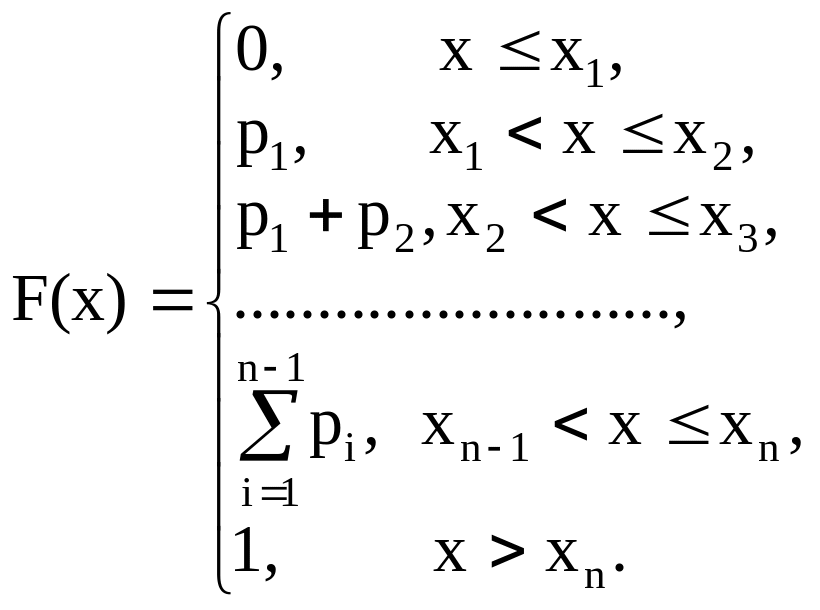(17)

График функции распределения ДСВ представляет собой ступенчатую линию (рис. 1).

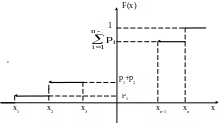
Рис. 1

Законом (или рядом) распределения ДСВ Х называют таблицу следующего вида:

Х	х 1 х2 х3 …	, (18)
P	р1 р2 р3 …

где х_i – возможные значения Х;

р_i = Р(Х = х_i); при этом

Графическое изображение закона распределения (18) называется многоугольником распределения. Для его построения в прямоугольной системе координат строят точки (х₁, р₁), (х₂, р₂), … и соединяют их отрезками прямых.

Закон распределения непрерывной случайной величины (НСВ) Х задается или функцией распределения, или функцией плотности вероятности. Функция распределения НСВ Х выражается формулой

(19)

где f(x) ≥ 0 – функция плотности вероятности.

Свойства плотности вероятности:

1. 

2. f(x) = F'(x);

3. Р(х₁ ≤ Х ≤ х₂) =

График функции распределения F(x) непрерывной случайной величины является непрерывной кривой. График функции плотности называется кривой распределения.

Характеристиками положения случайной величины являются математическое ожидание, мода и медиана.

Математическим ожиданием случайной величины Х называют число М(Х), определяемое соответственно формулами (предполагается, что ряд и интеграл сходятся абсолютно):

(20)

где Х – дискретная случайная величина;

х_i – значения случайной величины;

р_i – их вероятности;

M(Х) = (21)

где Х – непрерывная случайная величина,

f(x) – плотность вероятности.

Свойства математического ожидания:

1. М(С) = С, где С – const;

2. М(СХ) = С М(Х);

3. М(Х±Y) = M(X) ± M(Y), где Х и Y – любые случайные величины;

4. М(Х∙Y) = M(X) ∙ M(Y), если Х и Y – независимые случайные величины.

Случайные величины Х и Y называются независимыми, если для любых х и y имеет место

P(X < x, Y < y) = P(X < x) ∙ P(Y < y). (22)

Модой (М₀) ДСВ называется ее наиболее вероятное значение. Модой НСВ называется то ее значение, при котором плотность вероятности максимальна.

Медианой НСВ Х называется такое ее значение М_е, для которого

P(X < M_e) = P(X > M_e) = (23)

Дисперсия определяется как математическое ожидание квадрата отклонений случайной величины от своего математического ожидания

D(X) = M(X – M(X))². (24)

Для вычислений удобна также следующая формула:

D(X) = M(X²) – (M(X))². (25)

Свойства дисперсии:

1. D(C) = 0, где С – const;

2. D(CX) = C² D(X);

3. если Х и Y – независимые случайные величины, то D(X ± Y) = D(X) + D(Y).

Дисперсия ДСВ Х, имеющей распределение (18), вычисляется по формулам:

или (26)

(27)