3.2. Прохождение частицы через потенциальный барьер о Рис.4.1 сновные формулы

Коэффициенты преломления n, отражения R и пропускания D волн де Бройля для низкого потенциального барьера (U<E) бесконечной ширины

,

,

где ₁ и ₂ - длины волн, де Бройля в областях 1 и 2 (частица движется из области 1 в область 2); k₁ и k₂ - соответствующие значения волновых чисел.

Коэффициент отражения для высокого (U>E) потенциального барьера бесконечной ширины

.

Коэффициент прозрачности D прямоугольного потенциального барьера конечной ширины

,

где U - высота потенциального барьера; Е-энергия частицы; m-масса частицы; d-ширина барьера.

Примеры решения задач

1

. Частица с массой m и энергией Е движется в направлении низкого по­тенциального барьера бесконечной ширины. Найти выражение для коэф­фициента отражения R и коэффициента прохождения D этого барьера.

Решение

Направим ось Ox в направлении движения частицы (рис. 3.2) будем счи­тать, что потенциальная энергия определяется условиям U=0, если x<0 (область 1); U=U₀, если x>0 (область 2). Стацио­нарные уравнения Шредингера, описы­вающие движения частиц в соответст­вующих областях, будут иметь следующий вид:

, (1)

. (2)

Введя обозначения

,

получим

, (3)

. (4)

Решением данных уравнений являются функции

, (5)

. (6)

Эти функции после умножения на временной мно­житель будут представлять собой суперпозицию волн де Бройля, распространяющихся в обе стороны, а квадраты их амплитуд - интенсив­ности этих волн.

В области 1 распространяются как падающая, так и отраженная волны с интенсивностями = (A₁)₂ и = (В₁)₂. В области 2 распространяется толь­ко проходящая волна, поэтому В₂= 0.

Предположим, что амплитуда падающей волны А₁ =1, и вычислим ам­плитуды В₁ и А₂. Воспользовавшись условиями непрерывности пси-функции и ее производной

, .

Получим:

А₁ + В₁ = А_2, (7)

К₁(А₁-В₁) = К₂А_2. (8)

Решение данной системы дает следующие выражения для искомых коэф­фициентов:

, (9)

. (10)

Коэффициент отражения R, определяющий вероятность отражения частицы от потенциального барьера, выражается формулой

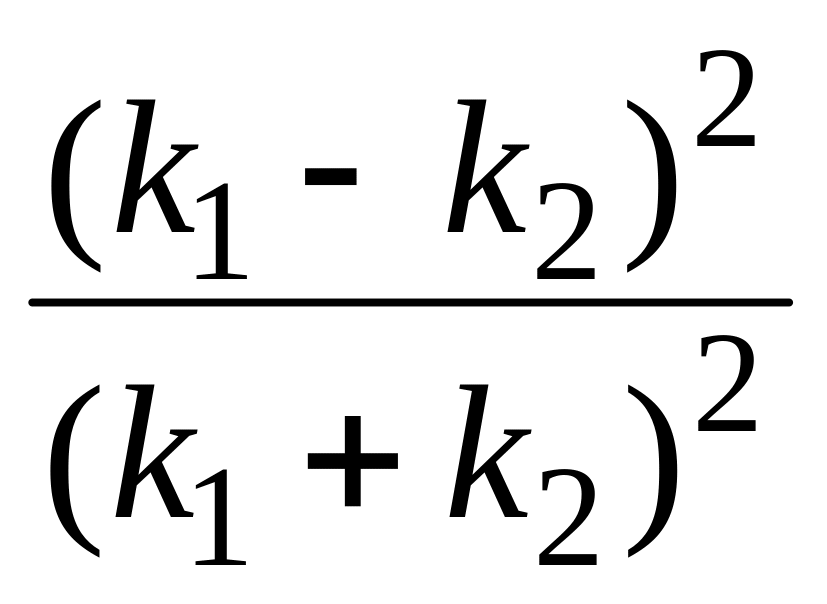= . (11)

На основании закона о сложении вероятностей можно утверждать с достоверностью, что налетающая на барьер частица либо отразится от него, либо пройдет далее, т.е. выполняется условие , где D – коэффициент прохождения частицы через барьер. Учитывая данное соотношение, найдем выражение для коэффициента прохождения частицы

.

На рис. 3.3 изображена действительные части па­дающей волны ( ) и прошедшей волны ( ). Выполнение ус­ловий непрерывности пси-функции и ее производной приводит к плавному со­пряжению косинусоид.

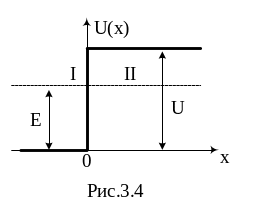
Задача 2. На высокий потенциальный барьер U бесконечной ширины падает поток частиц с энергией Е<U (рис. 3.4). Установить выражение для плотности веро­ятности нахождение частицы на расстоянии x от границы барьера.

Решение

Для высокого потенциального барьера в области x<0, уравнение Шредингера имеет вид

, (1)

а его решение

. (2)

В области x>0 уравнение Шредингер запишется следующим образом

. (3)

Решение данного уравнения имеет вид

. (4)

Воспользовавшись условиями непрерывности волновой функции и ее первой производной в точке x=0, получим систему уравнений,

(5)

,

из которых следует, что амплитуда отраженной волны равна

, (6)

где .

Вычисления модуля амплитуды отраженной волны дают единицу, из чего следует, что в стационарном состоянии вся энергия падающей волны отражается, но под «ступенькой» существует экспоненциально затухающая волновая функция с амплитудой

. (7)

Н а рис.3.4 изображены действительная часть падающей волны де Бройля движущейся частицы в области 1 и экспоненциально убывающая волновая функция в области 2.

3. Электрон с энергией Е=9 эВ движется на прямоугольный потенци­альный барьер высотой U=10 эВ и шириной d=0,1 нм. Определить коэффициент прозрачности барьера. Представить на графике вид волновой функции электрона.

Решение

Рассмотрим движение электрона вдоль оси x и выделим 3 области (рис 3.5), в которых по­тенциальная энергия электрона имеет следующие значения:

при - (обл. 1)

при 0 (обл. 2)

при (обл. 3)

Уравнение Шредингера для областей 1 и 3 имеет вид

А для области 2

Пренебрегая отраженными волнами на границах раздела 1-2 и 2-3, решения данных дифференциальных уравнений можно представить в следующем упрощенном виде

, (1)

, (2)

. (3)

Коэффициент Α1 в выражении (1) связан с интенсивностью пучка частиц, движущихся к барьеру, и принимается, как обычно, равным единице, а значения других коэффициентов с учетом принятых упрощений будут следующими

А₂≈ А₁=1 и А₃≈А₂e^-kd . (4)

Коэффициент А₃ представляет амплитуду волновой функции, прошедшей через барьер, а отношение квадратов модулей амплитуд прошедшей и падающей волны определяет вероятность прохождения частиц через барьер, т.е. коэффициент прозрачности

(5)

Подстановка численных значений дает D 0,2.

Вид пси-функций Ψ₁(x), Ψ₂(x), Ψ₃(x) представлен на рис. 3.6. Волновая функция частицы всюду непрерывна и гладко переходит из одной области в другую. В области барьера она экспоненциально уменьшается при изменении x от нуля до d. Поскольку волновые числа в области I и III одинаковы, длины волн де Бройля также одинаковы и равны

Р ис. 3.6