4.2.4. Темы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами

№ п/п	Наименование обеспечиваемых (последующих) дисциплин	№ тем данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин
		1	2	3	4	5	6	7	8	…
1.	Теория вероятностей и математическая статистика	+				+	+	+
2.	Эконометрика				+
3.	Экономико-математическое моделирование	+		+	+	+	+	+	+

5. Образовательные технологии

Удельный вес занятий, проводимых в интерактивных формах, определяется главной целью (миссией) программы, особенностью контингента обучающихся и содержанием конкретных дисциплин, и в целом в учебном процессе они должны составлять не менее ___% аудиторных занятий (определяется требованиями ФГОС с учетом специфики ООП). Занятия лекционного типа для соответствующих групп студентов не могут составлять более ___% аудиторных занятий (определяется соответствующим ФГОС)).

Показатель	Требования ФГОС, %	Фактически, %
Удельный вес активных и интерактивных форм проведения занятий (компьютерных симуляций, деловых и ролевых игр, разбор конкретных ситуаций, психологические и иные тренинги), %	Не менее __20__	40
Удельный вес занятий лекционного типа, %	Не более ___20_	20

6. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов

_____________________________________________________________________________

(Указываются темы эссе, рефератов, курсовых работ и др. Приводятся контрольные вопросы и задания для проведения текущего контроля и промежуточной аттестации по итогам освоения дисциплины, а также для контроля самостоятельной работы обучающегося по отдельным разделам дисциплины).

6.1. Оценочные средства для текущего контроля успеваемости

Вопросы для самопроверки (по темам)

1. Общие понятия о множествах.

2. Числовые множества. Множество действительных чисел. Абсолютная величина действительного числа. Окрестность точки.

3. Понятие функции. Элементарные и неэлементарные функции. Примеры.

4. Основные элементарные функции, их классификация. Примеры.

5. Способы задания функций. Примеры.

6. Предел числовой последовательности. Определение. Примеры.

7. Предел функции. Основные теоремы о пределах. Пояснения.

8. Неопределенные выражения, их природа. Примеры.

9. Бесконечно малые и бесконечно большие величины. Примеры.

10. «Замечательные» пределы. Понятие эквивалентных бесконечно малых величин. Таблица эквивалентных.

11. Примеры вычисления пределов функций с помощью таблицы эквивалентных бесконечно малых.

12. Непрерывность функции. Точки разрыва. Примеры.

13. Определение производной. Таблица производных основных элементарных функций.

14. Правила дифференцирования. Примеры.

15. Дифференцирование сложной функции. Примеры.

16. Дифференцирование обратной функции. Примеры.

17. Логарифмическое дифференцирование. Применение для вычисления производных. Примеры.

18. Производная функции, заданной неявно. Примеры.

19. Применение правила Лопиталя к раскрытию неопределенностей. Пример.

20. Понятие первообразной функции (неопределенного интеграла).

21. Таблица основных первообразных функций.

22. Примеры интегралов, не выражающихся через элементарные функции в конечном виде («не берущихся» интегралов).

23. Метод непосредственного интегрирования. Примеры.

24. Метод замены переменной (подстановки) в неопределенном интеграле. Пример.

25. Формула интегрирования по частям в неопределенном интеграле. Пример применения.

26. Интегрирование выражений, содержащих рациональные функции от тригонометрических функций. Универсальная тригонометрическая подстановка. Пример.

27. Понятие определенного интеграла. Его геометрический смысл.

28. Основная формула интегрального исчисления (формула Ньютона-Лейбница). Пример применения.

29. Замена переменной в определенном интеграле. Пример.

30. Формула интегрирования по частям в определенном интеграле. Пример применения.

Примерные темы эссе, рефератов и др.

1.История развития дифференциального и интегрального исчисления.

2.История развития задач математики, экономики, техники, приводящие к решению дифференциальных уравнений.

3.Решение некоторых задач математического анализа вероятностными методами.

4.Обзор современных программных средств для решения задач математического анализа.

5.Математическая экономика с применением программных средств.

Примерные задания для контрольных работ

1. Вычислить пределы функций:

а). ;

б). ;

в). .

2. Найти производные следующих функций:

а). ;

б). ;

в). .

3. Вычислить неопределенные интегралы:

а). ;

б). ;

в). .

IV. Вычислить определенные интегралы:

а). ;

б). ;

в). .

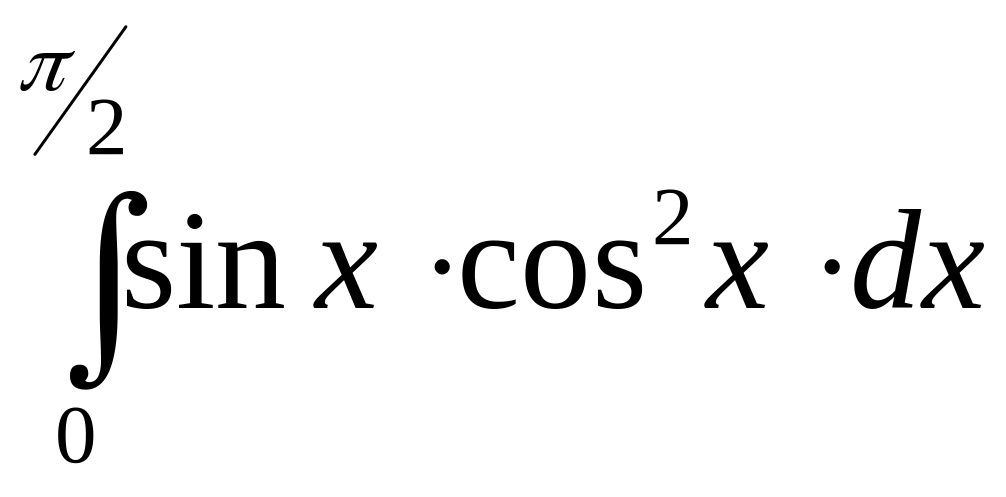5. Проинтегрировать следующие линейные дифференциальные уравнения:

а). ;

б). .

5. Решить задачу Коши:

, если: при .

5. Решить следующую краевую задачу:

, если:

при , при .