Пример 1.

Требуется найти передаточную функцию для цепи, приведенной на рис.6.8. Четырехполюсник задан Z-параметрами.

Данная цепь описывается следующими четырьмя уравнениями

и х которых первые два описывают четырехполюсник, третье – генератор, а четвертое – нагрузку. Решим записанную систему уравнений относительно переменной . Такое решение проще всего получить с помощью сигнального графа, построенного по системе уравнений (рис.6.12). Пользуясь формулой Мэзона, получим:

,

где - определитель матрицы Z-параметров.

Отсюда

. (6.27)

Если в полученной формуле положить и учесть, что при этом , найдем коэффициент передачи напряжения для схемы рис.6.11,а:

. (6.28)

Пример 2.

Требуется найти входное сопротивление четырехполюсника, нагруженного на сопротивление рис.6.9,б.

Для этого случая достаточно решить относительно переменной систему из трех уравнений:

к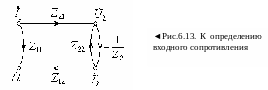 оторой соответствует граф, приведенный на рис.6.13. По формуле Мэзона получаем:

,

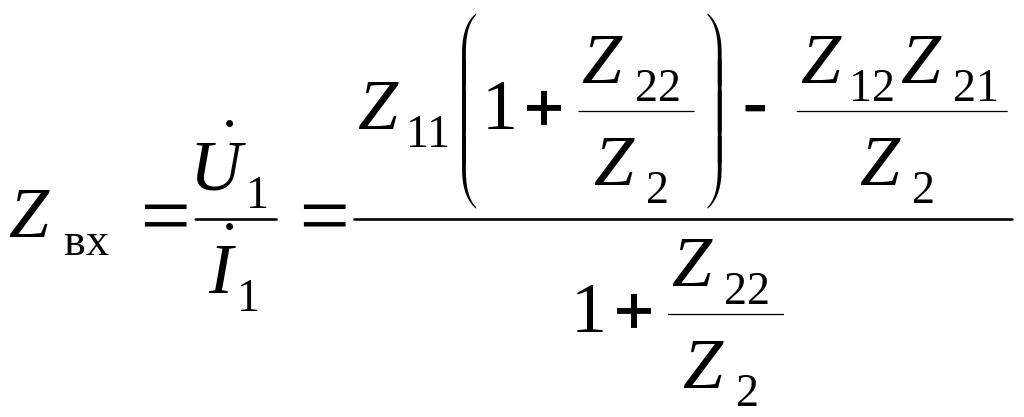или

. (6.29)

6.1.4. Принципы измерения z-параметров четырехполюсника

В настоящей лабораторной работе Z-параметры четырехполюсника измеряются в соответствии с их физическим смыслом, определяемым формулами (6.7)-(6.10). Рассмотрим сначала измерение . Для этого перепишем (6.7) в виде

.

Здесь

, . (6.30)

Из (6.30) следует, что для экспериментального определения достаточно взять отношение измеренных действующих значений входного напряжения и входного тока в режиме холостого хода, а для определения нужно измерить сдвиг фаз между входным напряжением и входным током в том же режиме.

При измерениях на высоких частотах нет возможности прямого измерения тока, так как соответствующие амперметры промышленностью не выпускаются. Поэтому используется косвенное измерение тока с применением вольтметра и известного активного сопротивления. Введение в схему токосъемных сопротивлений необходимо также для подключения фазометра, если последний измеряет сдвиг фаз между напряжением и током или между двумя токами. В качестве фазометра может быть использован двухлучевой осциллограф. Предполагается, что измерение фазового сдвига производится по сдвигу осциллограммы одного гармонического колебания по отношению к осциллограмме другого.

Схема для измерения параметра представлена на рис.6.14. Четырехполюсник возбуждается генератором синусоидального напряжения. Выход четырехполюсника разомкнут. Входной ток находится по измеренному электронным вольтметром V₁ напряжению на известном токосъемном сопротивлении . Напряжение на входе измеряется электронным вольтметром V₂. Для измерения сдвига фаз используется двухлучевой осциллограф. Необходимо обратить внимание на соединение корпусов измерительных приборов в одной точке . В данном случае каждый из двух зажимов измерительного генератора должен быть изолирован от корпуса.

Очевидно

,

где и - показания соответствующих вольтметров.

Так как комплекс напряжения, подаваемого на первый вход осциллографа, выражается как , сдвиг фаз между напряжениями на втором и первом входах осциллографа равен

,

откуда

.

Выбор знака перед в этой формуле производится из соображения удобства.

Если в схеме рис.6.14 поменять местами зажимы и , то может быть измерен параметр .

Рассмотрим измерение параметра :

,

где

, . (6.31)

Схема для измерения модуля и аргумента параметра приведена на рис.6.15. Подобно предыдущему случаю для этой схемы получаем:

;

,

где - сдвиг фаз между напряжениями на втором и первом входах осциллографа. При перемене мест зажимов и четырехполюсника тем же способом измеряется модуль и аргумент параметра .