6.1.2. Основные уравнения линейного неавтономного четырёхполюсника
Для
составления уравнений четырёхполюсника
в установившемся гармоническом режиме
необходимо принять положительные
направления токов и напряжений.
Используются три варианта положительных
направлений, показанные на рис.6.6, причём
варианты а и б называются
соответственно вариантами прямой и
обратной передачи. Токи
,
а также
отличаются лишь знаком.
Линейность пассивного или неавтономного
активного четырёхполюсника является
достаточным основанием записи связей
между четырьмя переменными, а именно
двумя напряжениями
и двумя токами
(или
),
(или
),
в виде пары линейных алгебраических
уравнений. Указанные связи могут быть
выражены шестью способами (число
сочетаний из четырёх переменных по
две). Таким образом, различают шесть
систем уравнений четырёхполюсника.
Каждая из систем уравнений носит название
по виду параметров, которые связывают
между собой токи и напряжения
четырёхполюсника:
Y-уравнения передачи
;
(6.1)
Z-уравнения передачи
;
(6.2)
Н-уравнения передачи
;
(6.3)
G-уравнения передачи
;
(6.4)
А-уравнения передачи
;
(6.5)
В-уравнения передачи
.
(6.6)
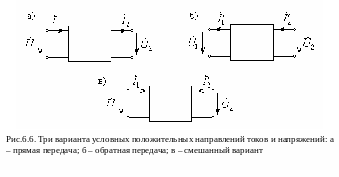
Заметим, что традиционным является использование в А-уравнениях передачи положительных направлений токов, соответствующих прямой передаче (рис.6.6,а), а в В-уравнениях передачи - направлений токов при обратной передаче (рис.6.6,б). Для остальных четырёх форм уравнений используется смешанный вариант положительных направлений токов (рис.6.6,в).
Каждая из систем уравнений передачи может быть записана в матричной форме. Например, система (6.2) будет иметь вид:
,
где
и
- матрицы-столбцы токов и напряжений
соответственно,
- квадратная матрица коэффициентов
уравнений, причём
.
Аналогично могут быть записаны и остальные системы уравнений.
Входящие в приведённые системы уравнений
коэффициенты называются параметрами
четырёхполюсника (первичными параметрами).
В этой связи говорят об Y-параметрах,
Z-параметрах, Н-параметрах и т.д. Легко
видеть, что за исключением частных
случаев все параметры четырёхполюсника
являются комплексными и частотнозависимыми.
Размерность любого параметра
устанавливается при рассмотрении
соответствующей формы уравнений. Так
из (6.1) - (6.4) следует, что все Y-параметры,
а также
имеют размерность проводимости (См),
все Z-параметры, а также
имеют размерность сопротивления (Ом),
а
и
безразмерны. Таким же образом
устанавливаются размерности других
параметров.
Физический смысл каждого параметра также устанавливается из рассмотрения соответствующей формы уравнений. Укажем, например, физический смысл Z-параметров. Полагая в правой части уравнений (6.2) один из токов равным нулю, получаем:
(6.7)
- входное сопротивление четырёхполюсника при разомкнутом выходе;
(6.8)
- передаточное сопротивление в режиме обратной передачи при разомкнутом входе;
(6.9)
- передаточное сопротивление в режиме прямой передачи при разомкнутом выходе;
(6.10)
- выходное сопротивление четырёхполюсника при разомкнутом входе;
В связи с тем, что Z-параметры четырёхполюсника определяются при условиях размыкания входа или выхода, эти параметры называются сопротивлениями холостого хода.
Принципиально достаточно пользоваться
только одной системой уравнений
четырёхполюсника и соответственно
одной системой параметров. Однако при
решении конкретных задач бывает
целесообразно использовать не любую
систему параметров, а лишь вполне
определённую, наиболее удобную для
решения данной задачи. Более того, при
решении одной задачи бывает целесообразно
последовательно применять разные
системы уравнений на отдельных этапах
решения. Предпочтительность некоторой
системы параметров перед другими
определяется спецификой решаемой задачи
и, возможно, относительной простотой
измерения параметров. Таким образом,
нередко возникает необходимость перехода
от одной системы параметров к другой.
Поясним такой переход следующими
примерами. Пусть известны Y-параметры
четырёхполюсника, и нужно найти параметры
и
.
Рассматривая уравнения (6.1) как уравнения
с двумя неизвестными
и
,
решим их относительно этих неизвестных.
При этом получаются уравнения в
Z-параметрах (6.2). Можно заметить, что
уравнения (6.1) и (6.1) являются обратными.
Поэтому матрица Z-параметров обратна
матрице Y-параметров:
,
(6.11)
где
- определитель матрицы
.
Если в (6.1) сделать подстановку
и решить полученную систему уравнений
относительно
,
то придём к уравнениям:
,
которые по форме являются А-уравнениями передачи (6.5). Отсюда можно записать матрицу :
.
(6.12)
Следует
заметить, что возможны вырожденные
случаи четырёхполюсников, когда некоторые
системы параметров не существуют (все
элементы матрицы получаются бесконечными).
Если, например, существуют Y-параметры,
а матрица
является вырожденной, то есть
,
то Z-параметры не существуют, так как
(6.11) не имеет смысла в силу деления на
нуль.
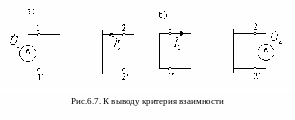
Установим теперь критерии взаимности и симметрии четырёхполюсника, выраженные через Y-параметры. По определению, для взаимного четырёхполюсника справедлива теорема взаимности, то есть для схем, приведённых на рис.6.7,а,б, выполняется равенство:
Таким образом, если четырёхполюсник является взаимным, то
(6.13)
(справедливо также и обратное утверждение).
Любой симметричный двухполюсник
является взаимным. Поэтому для
симметричного четырёхполюсника условие
(6.13) всегда выполняется. Кроме того, так
как для симметричного четырёхполюсника
посредством измерений нельзя установить
разницу между входом и выходом, должно
выполниться условие
.
Поэтому критерий симметрии четырёхполюсника
следующий
.
(6.14)
Если пересчитать любую систему параметров в Y-параметры, то с помощью (6.13) и (6.14) можно установить критерии взаимности и симметрии, выраженные через другие параметры четырёхполюсника. В частности, из формул (6.13), (6.14) и (6.11) следует, что для взаимного четырехполюсника
,
(6.15)
а для симметричного
.
(6.16)