3.4. Последовательное соединение r, l, c .

Пусть имеется цепь с последовательно соединенными элементами RLC (рис. 11), и по цепи протекает синусоидальный ток:

Согласно второго закона Кирхгофа:

Для оценки соотношений между действительными значениями напряжений на элементах, построим векторную диаграмму (рис. 12).

Для этого вектор тока отложим в произвольном направлении. Далее откладываем падение напряжения на всех элементах:

1. Напряжение на резистивном элементе совпадает по направление с током .

2. Напряжение на индуктивном элементе опережает по направлению ток на 90⁰.

3. Напряжение на емкостном элементе отстает по направлению от тока на 90⁰.

Из векторной диаграммы:

где

– полное сопротивление цепи, а выражение U = Iz закон Ома для цепи синусоидального тока.

Угол  показывает сдвиг по фазе между током и напряжением на зажимах.

В приведенном примере напряжение опережает ток на  , т.к. x_L > x_C и режим работы цепи активно-индуктивный.

Если бы x_L < x_C, то ток бы опережал напряжение на  и режим работы был бы активно-емкостным.

Если x_L = x_C, то ток совпадает с напряжением по фазе и режим работы тогда активный, в цепи имеет место резонанс.

Для оценки соотношений между активным, реактивным и полным сопротивлениями используют треугольник сопротивлений (рис. 13):

Реактивное сопротивление x = x_L - x_C.

Из этого треугольника следует:

Некоторые свойства последовательно соединённых элементов, рассмотрим на конкретном примере электрической цепи, приведенной на рис. 14.

Вычертим векторную диаграмму этой цепи (рис. 15).

В ектор тока откладываем в произвольном направлении. Далее откладываем падение напряжения на всех элементах: напряжения и ток на резистивном элементе совпадают по фазе, напряжение на индуктивном элементе по фазе опережает ток на , ток на емкостном элементе опережает напряжение на .

Используя векторную диаграмму можно определить величину напряжения на любом участке электрической цепи и его сдвиг по фазе относительно тока.

В общем случае суммарное падение напряжения на резистивных элементах равно , на индуктивных элементах - , на емкостных элементах - . Таким образом, последовательно соединённые резистивные, индуктивные и емкостные можно заменить эквивалентными. Они соответственно равны:

.

Тогда полное сопротивление всей ветви, соответственно равно:

В общем случае, при последовательном соединении резистивного, индуктивного и емкостного элементов, напряжение на зажимах цепи, можно разбить на две составляющие напряжения активную и реактивную (рис. 16).

Из векторной диаграммы следует: , .

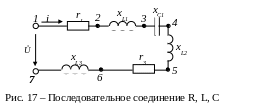
Рассмотрим порядок расчета на конкретном примере (рис. 17). Принимаем U = 120 (B), ω = 314 (рад/с), r₁ = 10 (Ом), r₃ = 14 (Ом), L₁ = 40 (мГн), L₂ = 35 (мГн), L₃ = 45 (мГн), С₁ = 90 (мкФ).

1. Определяем омические сопротивления реактивных элементов:

(Ом),

(Ом),

(Ом),

(Ом).

2. Определяем полное сопротивление ветви.

   1. Эквивалентное активное сопротивление

(Ом).

2. Эквивалентное индуктивное сопротивление

(Ом).

3. Эквивалентное емкостное сопротивление

(Ом).

2.4. Полное сопротивление

(Ом).

3. Определяем ток в цепи (А).

4. Определяем напряжения на каждом элементе цепи

(В),

(В),

(В),

(В),

(В),

(В).

5. Для построения векторной диаграммы принимаем масштаб по напряжению, Вычерчиваем векторную диаграмму рассматриваемой цепи (рис. 18).