Обчислюють ;

.

3. Магнітна індукція кожної ділянки

і т. д . Результати заносять у табл. 13.1.

4. За кривими намагнічування , і за відомим визначають для кожної ділянки. (по для сталі Е11; рис. 13.1) і т.д. Для повітряних зазорів

Результати заносять у табл. 13.1.

5. Добуток для кожної ділянки

і т. д .

6.Згідно з другим законом Кірхгофа для магнітного кола

.

За умовою задачі.

Отже, намагнічуючий струм котушки

7. Потокозчеплення та індуктивність котушки

.

Таким чином, для збудження заданого робочого магнітного потоку у котушці має проходити струм . При цьому індуктивність котушки буде .

8. Обчислимо струм тієї самої котушки, в тому самому магнітному колі, але без повітряних зазорів (якір притягнутий до осердя). Якщо , то

.

Отже,

Таким чином, для збудження такого самого робочого магнітного потоку у такому самому магнітному колі, але без повітряного зазора, необхідний струм , тобто у

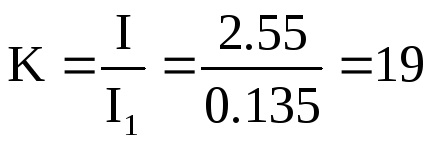разів менший.

9.Індуктивність котушки без повітряного зазору. Потокозчеплення залишається незмінним. Індуктивність

,

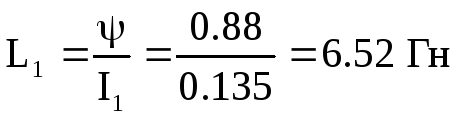Тобто без повітряного зазору індуктивність котушки збільшиться в

разів.

13.1.2. Обернена задача

Вихідні дані для розрахунку. Задається схема магнітного кола, (наприклад, рис. 13.7) і його геометричні розміри, а також матеріал осердя і якоря, МРС .

Знайти робочий магнітний потік .

Розв’язaння.

Якщо потоком розсіювання знехтувати, то повний потік . Якщо потік розсіювання слід урахувати, то його беруть , тобто . Але це визначається після розв’язування задачі, тобто тоді, коли буде знайдений основний потік .

Безпосередньо розв’язати задачу не вдається, оскільки невідомі магнітний потік , магнітна індукція , напруженість магнітного поля на окремих ділянках. Задачу можна розв’язати двома способами.

І спосіб (напіваналітичний). Задача розв’язується в кілька етапів. Суть розв’язування полягає в тому, що на кожному етапі задаються довільним значен-ням магнітного потоку . Так, на першому етапі задаються потоком і роз-в’язують пряму задачу. Знаходять , що відповідає потоку .

На другому етапі задаються потоком і знаходять , на третьому - потоком і знаходять і т.д. Етапів має бути стільки, щоб можна було побудувати залежність (рис. 13.9).

На кривій (рис. 13.9) по заданій МРС знаходиться шуканий потік . Якщо потрібна достатня точність розв’язку, то знову перевіряють аналітично за і розв’язують пряму задачу. В результаті мають здобути .

Рис.13.9

4.Знаходимо вебер-амперну характеристику всього магнітного кола як послідовного з’єднання першої ділянки кола ділянки магнітопроводу із загальною ділянкою другої та третьої ділянок, а також повітряного зазора (що знайдено в п.3). Характеристики додаємо при однакових магнітних потоках (рис. 13.22).

5. За знайденою у п.4 загальною вебер-амперною характеристикою і заданою намагнічуючою силою знаходимо магнітний потік (рис. 13.22).

6. Згідно з першим законом Кірхгофа для магнітних кіл у даній задачі (рис. 13.16) .

Отже, знаючи повний потік , можна знайти його складові частини і , використовуючи характеристики на рис. 13.21. Знайдений відкладаємо на осі ординат і проводимо горизонталь до перетину її з характеристи-кою . Потім опускаємо перпендикуляр на вісь абсцис. З точок перетину перпендикуляра з характеристиками і проводимо горизонталі до осі ординат, де і знаходимо і . Задачу розв’язано.