- •Содержание
- •1. Множества 10
- •2. Математическая логика 39
- •3. Теория графов 96
- •Тема 1. Множества 168
- •Тема 2. Математическая логика 169
- •Тема 3. Теория графов 171
- •Множества
- •1.1. Операции над множествами. Мощность множеств. Отображение множеств
- •Упражнение 1.1.1
- •Упражнение 1.1.2
- •1.2. Отношения на множествах
- •Будет ли пустое множество V каким-либо подмножеством некоторого множества?
- •Математическая логика
- •2.1. Алгебра высказываний
- •Логические операции
- •Функции алгебры высказываний
- •2.2. Проблемы разрешимости. Нормальные формы Логические отношения
- •2. Отношение эквивалентности.
- •3. Несовместимость.
- •Проверка правильности рассуждений
- •Нормальные формы формул алгебры высказываний
- •Совершенные нормальные формы
- •Построение формулы алгебры высказываний по заданной логической функции
- •Моделирование алгебры высказываний с помощью релейно-контактных схем
- •2.3. Исчисление высказываний Символы, формулы, аксиомы исчисления высказываний. Правила вывода
- •Теорема дедукции
- •Проблемы непротиворечивости, полноты, независимости аксиом исчисления высказываний
- •2.4. Логика предикатов
- •Кванторы
- •Кванторы как обобщение логических связок.
- •Отрицание кванторных предикатов
- •Теория графов
- •3.1. Графы
- •Степень вершины графа. Число ребер графа
- •Связность
- •Эйлеровы и гамильтоновы цепи и циклы. Теоремы Эйлера
- •Изоморфизм графов
- •Планарность. Плоские графы
- •Числа, характеризующие граф
- •Операции над графами. Объединение графов
- •Пересечение (произведение) графов
- •Прямое произведение графов
- •Матрицы для графов
- •Матрица инциденций
- •Матрицы достижимостей и контрадостижимостей
- •3.2. Деревья
- •Постановка задачи
- •Алгоритм Краскала
- •3.3. Экстремальные задачи на графах Задача о кротчайшем пути между двумя вершинами ориентированного графа и ее экономическая интерпретация
- •Алгоритм
- •Сети. Отношение порядка между вершинами ориентированного графа
- •Задача о пути максимальной длины между двумя вершинами ориентированного графа в сетевом планировании
- •Алгоритм
- •Сетевое планирование. Скорейшее время завершения проекта
- •Контрольное задание №1
- •Контрольное задание №2
- •Контрольное задание №3
- •Контрольное задание №4
- •Контрольное задание №5
- •Контрольное задание №6
- •Контрольное задание №7
- •Контрольное задание №8
- •Контрольное задание №9
- •Контрольное задание №10
- •Контрольное задание №11
- •Контрольное задание №12.
- •Контрольное задание №13.
- •Контрольное задание №14.
- •Контрольное задание №15
- •С писок рекомендуемой литературы
- •Интернет-ресурсы
- •Тема 2. Математическая логика
- •Тема 3. Теория графов
Контрольное задание №15
Строится нефтепровод, соединяющий города х1……x11. Стоимость возможных участков строительства задана таблицей.
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х7 |
х8 |
х9 |
х10 |
х11 |
х1 |
0 |
6 |
|
10 |
|
|
|
|
|
|
|
х2 |
|
0 |
6 |
|
8 |
6 |
|
|
|
|
|
х3 |
|
|
0 |
|
|
|
11 |
|
|
|
|
х4 |
|
|
|
0 |
3 |
|
|
|
|
5 |
|
х5 |
|
|
|
|
0 |
9 |
|
4 |
|
|
|
х6 |
|
|
|
|
|
0 |
|
|
|
|
|
х7 |
|
|
|
|
|
|
0 |
|
12 |
|
|
х8 |
|
|
|
|
|
|
|
0 |
|
7 |
|
х9 |
|
|
|
|
|
|
|
|
0 |
11 |
10 |
х10 |
|
|
|
|
|
|
|
|
|
0 |
9 |
х11 |
|
|
|
|
|
|
|
|
|
|
0 |
Изобразить схему нефтепровода, стоимость строительства которого минимальна, и подсчитать минимальные затраты.
Каждый из шести городов может быть соединен с другим участком газопровода, стоимость строительства которого указана в таблице.
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
х1 |
0 |
2 |
4 |
9 |
6 |
10 |
х2 |
|
0 |
3 |
3 |
9 |
7 |
х3 |
|
|
0 |
5 |
8 |
8 |
х4 |
|
|
|
0 |
7 |
10 |
х5 |
|
|
|
|
0 |
11 |
х6 |
|
|
|
|
|
0 |
Как построить самый дешевый нефтепровод, какова стоимость его строительства?
10 городов, обозначенных на графе вершинами х1…x10, необходимо соединить электролинией. Возможные соединения обозначены ребрами. Стоимость строительства на участке (хi,xj) обозначена соответствующим числом.
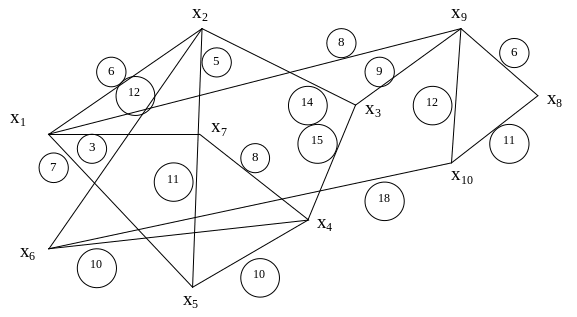
Определить стоимость строительства самой дешевой электролинии. Как она должна проходить?
На строительство электролинии между городами х1…..х7 отпущено 250 тысяч рублей. Стоимость строительства на возможных участках между городами хi,хj l(хi хj) в тыс. руб. задана следующим образом:
l(x1,x2)=40 l(x1,x3)=50 l(x1,x6)=60 l(x1,x7)=50 l(x2,x3)=30 |
l(x2,x6)=20 l(x2,x7)=30 l(x2,x4)=90 l(x3,x4)=60 l(x3,x7)=60 |
l(x4,x5)=90 l(x4,x7)=70 l(x5,x6)=80 l(x5,x7)=100 l(x6,x7)=10 |
Как построить электролинию, чтобы уложиться в эту смету?
Определить наименьшие затраты при перевозке груза из пункта х0 в пункт х6 через перевалочные пункты х1,х2,х3,х4,х5. Стоимость перевозки груза из пункта хi в хj указана на графе. Определить путь, соответствующий минимальной стоимости.
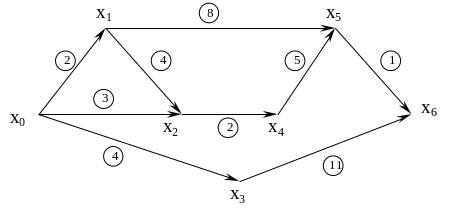
Из пункта А в пункт N перевозят однородный груз, используя перевалочные пункты В, С, D, Е, F, G. Расстояние между пунктами, соединенными дорогами, указаны на графе.
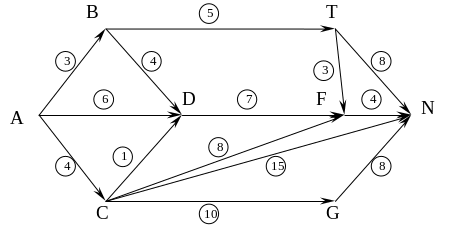
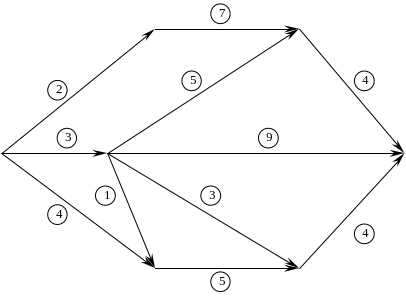
Определить кратчайший путь и его длину, предварительно пронумеровав вершины графа.
Пункты А и В связаны сетью дорог, проходящих через пункты С, D, Е, М, N. Стоимость проезда из пункта xi в xj указана на графе. Какова минимальная стоимость проезда из А и В?. Как проходит путь, соответствующий минимальным затратам?
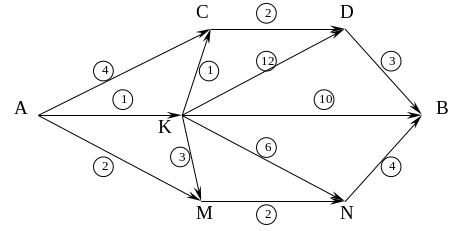
Для графов задач 6, 7 определить критический путь и критическое время.
Основу строительства объекта составляют 14 операций, последовательность выполнения которых задана графом. Продолжительность каждой из них указана на графе.
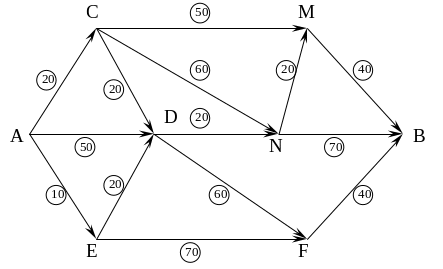
Определить скорейшее время завершения всего проекта. Какие операции не допускают запаздывания по времени?
Найти кратчайший и длиннейший пути, соединяющие вход и выход графа, предварительно правильно пронумеровав вершины.