Синтез свободного движения сау

Управляемый свободный процесс в системе определяется парой матриц A, B объекта управления и матрицей регулятора состояния, призванной обеспечивать оптимальность переходных свободных движений при произвольных начальных значениях вектора состояния X(0). На первом этапе синтеза будем полагать равными нулю все внешние аддитивные воздействия . Тогда управление свободным движением примет вид

(9.15)

Для нахождения матрицы воспользуемся теоремой об n интервалах дискретного управления в сочетании с принципом оптимальности Беллмана [10]. Не снижая общности выкладок, будем полагать, что оптимальное свободное движение системы завершается через n тактов дискретного управления в нулевой точке пространства состояний . Сформируем расширенный вектор-столбец состояния

V(t) = col [X(t), U(kT)] (9.16)

и перепишем уравнение для случая управляемого свободного движения в виде

(9.17)

где D – матрица управляемого состояния размерности (n+m)(n+m),

. (9.18)

Зададимся некоторой произвольной дискретной управляющей последовательностью U(kT), k = –1, –2, ... , –n и рассмотрим движение системы в обратном времени, т.е. примем конечное нулевое состояние системы за начальное. Проинтегрируем уравнение (9.17) при нулевых начальных условиях X(0) = 0, воспользовавшись аппаратом переходных матриц состояния, получим векторное дискретное уравнение состояния

(9.19)

где – расширенная обратная матрица перехода.

Сформируем матрицы дискретного управления W размерности и дискретного состояния G размерности в виде

W = [ U(-T) U(-2T) ... U(-nT) ] , (9.20)

G = [ X(-T) X(-2T) ... X(-nT) ] . (9.21)

Поскольку не наложены какие-либо ограничения на множества управляющих воздействий и дискретные состояния системы, а также, по определению, система находилась в нулевом начальном состоянии, очевидно, что ее движение в обратном (по отношению к принятому при синтезе) направлении будет носить оптимальный по быстродействию апериодический характер. Следовательно, с учетом выражения (9.15) искомую матрицу можно найти в виде

. (9.22)

Решение векторно-матричного уравнения (9.22) будет единственным при полном ранге матрицы G, т.е. если rank(G) = n.

Синтез вынужденного движения сау

На втором этапе синтеза определим матрицы , , входящие в выражение (9.19) для чего рассмотрим вынужденное движение системы.

Представим вектор-столбец установившихся состояний САУ в виде

(9.23)

где – подвектор размерности m1, определяющий заданное установившееся состояние системы, т. е. ,

– подвектор размерности (n-m)1, включающий в себя остальные координаты состояния системы управления.

Соответствующую матрицу установившихся состояний представим в виде блочной матрицы

(9.24)

где – подматрицы соответственно размерности .

Представим все аддитивные воздействия на систему в виде обобщенного вектора-столбца размерности (2m+d)1 задающих и возмущающих воздействий

(9.25)

и зададимся численными значениями его 2 компонент 2 раз, из которых сформируем неособую матрицу Q аддитивных воздействий размерностью (2m+d)(2m+d) в виде

. (9.26)

Тогда, с учетом введенных обозначений (9.14)…(9.25), уравнение (9.13) для квазиустановившихся состояний системы ( , ) можно переписать в виде

. (9.27)

Подставим векторы установившихся состояний в уравнение (10.19) и выразим искомую блочную матрицу

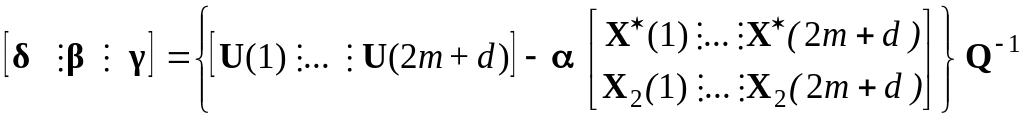(9.28) Матрицы , ,  определяются однозначно при полном ранге матрицы Q, что легко обеспечить соответствующим заданием значений аддитивных воздействий, либо формированием заведомо невырожденных матриц размерности (2m+d)(2m+d).

Таким образом, результирующее дискретное управление в форме (9.14) представляет собой цифровой регулятор состояния, обеспечивающий комбинированное апериодическое управление по отклонению выходной координаты от заданного значения и по возмущающим воздействиям, а также астатизм первого порядка по задающим воздействиям.