
- •Системы управления исполнительными механизмами
- •Оглавление
- •Принятые сокращения
- •Введение
- •Классификация и общее устройство исполнительных механизмов
- •1.1. Исполнительные механизмы. Основные понятия.
- •Классификация исполнительных механизмов
- •Электрические исполнительные механизмы
- •1.3.1. Исполнительные механизмы электрические однооборотные
- •Структура условного обозначения и основные параметры им мэо:
- •1.3.2. Исполнительные механизмы электрические многооборотные
- •1.3.3. Исполнительные механизмы электрические прямоходные
- •Пневматические исполнительные механизмы
- •Гидравлические исполнительные механизмы
- •Электрогидравлических клапанов
- •1.6. Электромагнитный исполнительный механизм
- •2.2. Обобщенные функциональные схемы, координаты и параметры суим. Функциональные элементы суим.
- •. Основные задачи исследования и стадии проектирования суим
- •2.3.1. Основные задачи исследования суим
- •2.3.2. Стадии проектирования суим
- •3. Математическое описание и характеристики суим
- •3.1. Формы математического описания линейных суим
- •3.2. Линеаризация нелинейных элементов суим
- •3.3. Статические и динамические характеристики суим
- •3.3.1. Статика суим. Коэффициенты ошибок суим по положению, скорости и ускорению
- •3.3.2. Динамика суим. Свободные и вынужденные переходные процессы
- •4. Общие Принципы работы и математические модели элементов суим
- •4.1. Исполнительные механизмы
- •4.2. Приводы
- •4.2.1. Коллекторные двигатели постоянного тока
- •4.2.2. Бесколлекторные двигатели постоянного тока
- •4.2.3. Асинхронные двигатели
- •4.2.4. Синхронные двигатели
- •4.2.5. Шаговые двигатели
- •4.3. Силовые преобразователи энергии
- •4.3.1. Электромашинные преобразователи
- •4.3.2. Тиристорные преобразователи
- •4.3.3. Транзисторные и симисторные преобразователи
- •4.4. Датчики координат суим
- •4.5. Регуляторы, корректирующие звенья
- •1. Пропорциональный регулятор (п-регулятор).
- •2. Интегральный регулятор (и-регулятор).
- •3. Дифференциальный регулятор (д-регулятор).
- •4. Пропорционально-интегральный регулятор (пи-регулятор).
- •6. Пропорционально-интегрально-дифференциальный регулятор (пид-регулятор).
- •5. Общие принципы построения суим
- •5.1. Релейно-контакторные суим
- •5.1.1. Рксу асинхронным двигателем с короткозамкнутым ротором
- •5.1.2. Рксу асинхронным двигателем с фазным ротором
- •5.2. Бесконтактные суим постоянной скорости
- •5.3. Системы стабилизации выходной координаты объекта управления. Типовые методы улучшения качества регулирования
- •В статике, т.Е. В установившихся (квазиустановившихся) режимах функционирования систем стабилизации можно сформулировать два основных тесно взаимосвязанных требования:
- •5.4. Системы программного управления, способы ограничения координат суим
- •5.5. Системы следящего управления, понятие добротности
- •6. Синтез суим
- •6.1. Подчиненное регулирование координат
- •6.2. Оптимальные настройки контуров регулирования
- •6.2.1. Технический оптимум
- •6.2.2. Симметричный оптимум
- •6.2.3. Апериодический оптимум
- •6.3. Типовая методика структурно-параметрического синтеза
- •7. Системы регулирования скорости эим
- •7.1. Система регулирования скорости “Тиристорный преобразователь - двигатель постоянного тока”
- •1. Синтез контура регулирования тока якоря.
- •2. Синтез контура регулирования скорости.
- •7.6. Переходный процесс в сар скорости при скачке задания
- •Р ис. 7.7. Переходные процессы в сар скорости при ударном приложении нагрузки на валу электропривода
- •7.2. Система регулирования скорости “Генератор - двигатель постоянного тока”
- •7.4. Системы управление эим переменного тока
- •8. Системы регулирования положения эим
- •8.1. Режимы перемещения рабочих органов
- •8.2. Сар положения с линейным регулятором
- •8.3. Сар положения с нелинейным регулятором
- •Подставляя в это соотношение выражение (8.2) для Kрп в режиме средних перемещений получим
- •8.4. Инвариантные и квазиинвариантные следящие суим
- •9. Дискретно-непрерывные суим
- •9.1. Дискретизация сигналов и z-преобразование
- •9.2. Дискретные передаточные функции и разностные уравнения при описании суим
- •9.3. Синтез цифровых систем управления
- •9.3.1. Методы дискретизации аналоговых регуляторов и билинейного преобразования
- •9.3.2. Метод переменного коэффициента усиления
- •9.3.3. Метод аналитического конструирования цифровых регуляторов состояния
- •Синтез свободного движения сау
- •Синтез вынужденного движения сау
- •10. Интеллектуальные суим
- •10.1. Функциональная структура интеллектуальной суим
- •10.2. Технические средства интеллектуализации суим
- •10.3. Суим на основе средств управления фирмы овен
- •Заключение
- •Список литературы
3.3.2. Динамика суим. Свободные и вынужденные переходные процессы
Динамические режимы СУИМ характеризуются переходными состояниями системы при изменении начального состояния, а также входных (задающих и (или) возмущающих) воздействий). При этом различают свободные и вынужденные переходные процессы.
Свободный (собственный) процесс в системе определяется решением однородного дифференциального уравнения, описывающего СУИМ, протекает под действием ненулевых начальных условий Y(t0) ≠ 0 и в устойчивых системах асимптотически затухает:
![]() ,
(3.17)
,
(3.17)
где ![]() – матрица перехода системы из начального
состояния Y(t0)
в текущее состояние Y(t).
– матрица перехода системы из начального
состояния Y(t0)
в текущее состояние Y(t).
Назовем процесс вынужденным, если промежуток времени между моментом tз (tв) приложения задающего (возмущающего) воздействия X(t) и моментом наблюдения выходной величины Y(t) равен бесконечности. В дальнейшем будем полагать моменты времени приложения воздействий равными нулю. Тогда процесс изменения выходной величины Y(t) в соответствие с теоремой свертывания (умножения изображений) будет иметь вид [9,10]
![]() , (3.18) где
, (3.18) где ![]() –
импульсная переходная функция по
задающему (возмущающему) воздействию.
–
импульсная переходная функция по
задающему (возмущающему) воздействию.
Полное решение уравнения движения линейных СУИМ представляет собой сумму решений уравнений свободного и вынужденного движений.
В теории управления к типовым тестовым воздействиям относят, как правило, единичное ступенчатое и единичное импульсное воздействия. Соответствующие динамические реакции систем на эти воздействия называют переходным процессом и импульсным переходным процессом.
В качестве примера на рис. 3.3 приведена реакция электродвигателя постоянного тока на ступенчатое приложение номинальной нагрузки Mсн к его валу (возмущающего воздействия).
При приложении номинальной нагрузки
скорость
![]() двигателя падает, причем имеет место
колебательный процесс. Максимальный
динамический провал скорости
двигателя падает, причем имеет место
колебательный процесс. Максимальный
динамический провал скорости
![]() превышает статическое падение скорости
превышает статическое падение скорости
![]() (см. рис. 3.1).
(см. рис. 3.1).
Вынужденное движение соответствует
новому установившемуся состоянию –
номинальной скорости
![]() электродвигателя. Время переходного
процесса (перехода в новое установившееся
состояние) составляет tрег
.
электродвигателя. Время переходного
процесса (перехода в новое установившееся
состояние) составляет tрег
.
З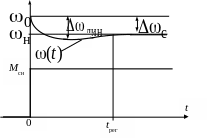 адача
исследования динамических свойств СУИМ
в концепции современной теории управления
решается путем решения векторно-матричного
уравнения состояния относительно
желаемой, как правило, выходной переменной
СУИМ. Для этой цели применяют матрицу
переходных состояний.
адача
исследования динамических свойств СУИМ
в концепции современной теории управления
решается путем решения векторно-матричного
уравнения состояния относительно
желаемой, как правило, выходной переменной
СУИМ. Для этой цели применяют матрицу
переходных состояний.
Рис. 3.3. Реакция электродвигателя постоянного тока на возмущающее воздействие в виде ступени номинальной нагрузки на валу
Если известны в момент времени t = 0 начальное состояние X(0) объекта управления и вектор управляющих воздействий U(0) (призванный оптимизировать движение системы), то уравнение движения системы во времени (здесь и далее полагается, что возмущения F(t), действующие на систему, равны нулю) определяется выражением [9,10]:
![]() . (3.19)
. (3.19)
Первое слагаемое в векторно-матричном выражении (3.12) отражает свободное движение многомерной линейной САУ и аналогично скалярному выражению (3.17), описывающему свободное движение одномерной системы. Второе слагаемое в (3.19) отражает вынужденное движение многомерной линейной САУ и аналогично выражению (3.18), описывающему вынужденное движение одномерной системы.
Матрицу
![]() ,
определяющую динамические процессы в
системе, называют переходной матрицей
состояния или просто матрицей перехода.
Существует ряд методов нахождения этой
матрицы, базирующихся на описании систем
как во временной области (в форме
дифференциальных или векторно-матричных
уравнений), так и в области комплексного
переменного p (в
операторной форме или в форме структурных
схем). Наиболее часто для определения
матрицы перехода во временной области
используют матричную экспоненциальную
функцию в виде разложения ее в ряд с
ограниченным числом k
(
,
определяющую динамические процессы в
системе, называют переходной матрицей
состояния или просто матрицей перехода.
Существует ряд методов нахождения этой
матрицы, базирующихся на описании систем
как во временной области (в форме
дифференциальных или векторно-матричных
уравнений), так и в области комплексного
переменного p (в
операторной форме или в форме структурных
схем). Наиболее часто для определения
матрицы перехода во временной области
используют матричную экспоненциальную
функцию в виде разложения ее в ряд с
ограниченным числом k
(![]() )
членов ряда [10]:
)
членов ряда [10]:
![]() , (3.20)
, (3.20)
где E – единичная матрица;
! – знак факториала.
Решение векторно-матричного уравнения, описывающего линейную систему управления, можно получить и в области комплексного переменного p, применив преобразование Лапласа:
![]() , (3.21)
, (3.21)
где ![]() – преобразование Лапласа переходной
матрицы состояния,
– преобразование Лапласа переходной
матрицы состояния,
т. е.
![]() .
.
В частности для свободного движения системы под действием ненулевого начального состояния X(0) можно записать
![]() . (3.22)
. (3.22)
