8.13. Оцінка результатів, що містять промахи і грубі похибки.
Наявність в ряду вимірювань декількох результатів з грубими відхиленнями повинно занепокоїти оператора і потребує аналізу їх причин. При цьому під сумнів може бути поставлений увесь ряд вимірювань.
Між результатами, що містять грубі відхилення, і результатами, які заслуговують довіри, буває важко провести границю.
Запропоновано ряд прийомів і формул для визначення результатів, які підлягають відкиданню.
Найбільш
простим прийомом є відкидання результатів,
які містять похибки більші, ніж
.
Щоб визначити, які результати підлягають відкиданню, необхідно попередньо опрацювати ряд вимірювань, включаючи всі результати, тобто обчислити середнє квадратичне відхилення S даного ряду.
Якщо середнє квадратичне відхилення для даного методу вимірювання було визначено раніше на основі вивчення великого ряду вимірювань, то з ним порівнюють середнє квадратичне відхилення S нового ряду. Потім визначають результати, які підлягають відкиданню на основі вибраного критерія, використовуючи вже відоме для нього СКВ. Якщо ж цього відхилення немає, то використовують СКВ даного ряду. Потім обчислення проводять знову вже з очищеним рядом. Якщо СКВ методу відомо, то з ним порівнюють нове значення СКВ ряду.
Викладений метод можна застосовувати тоді, коли відоме σ або коли S визначається на основі достатньо великої кількості вимірювань.
При малій кількості вимірювань більш точні результати дає критерій Романовського, який базується на розподілі Ст’юдента.
8.14. Критерій Романовського.
Нехай
виконано
вимірювань. При цьому n
результатів не викликають сумніву у
відношенні відповідності їх закономірному
ряду, а один результат здається таким,
що порушує цей ряд. Цей
результат ми позначимо через
.
Послідовність обробки результатів вимірювання в цьому випадку наступна:
1.
Знаходять середнє
арифметичне
значення для
результатів від
до
:
.
2. Знаходять середнє квадратичне відхилення (СКВ) окремого вимірювання:
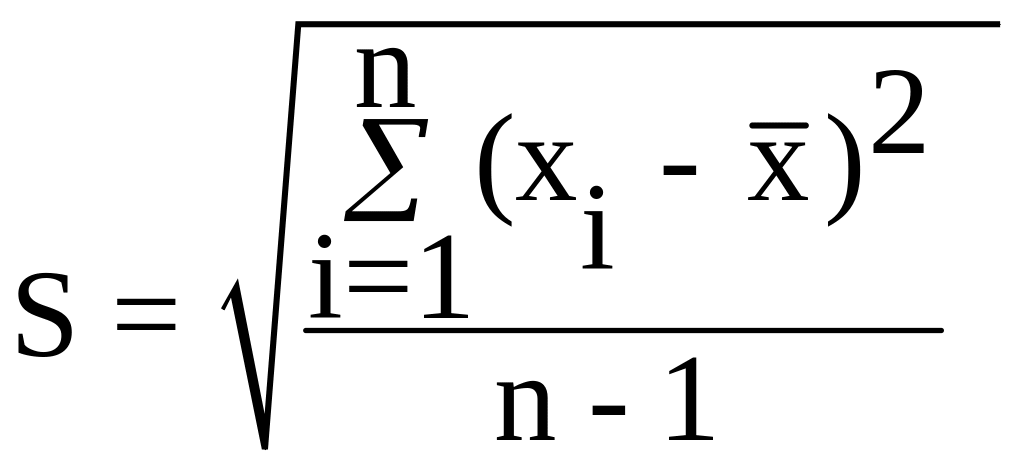
3.
Виходячи зі ступеня вірогідності, який
повинен бути забезпечений, задаються
імовірністю
того, що значення (
)
не перевищує деякого значення
,
яке потрібно визначити, тобто (
)
.+
4. Знаходять допустиме значення інтервалу (довірчий інтервал) з виразу:
Для
цього користуються
таблицею, в якій приведено значення
для
різних
і
n
(таблиця 8.1).
5. Якщо ( ) > , то результат підлягає виключенню з ряду результатів вимірювань.
Таблиця 8.1
Значення коефіцієнта для різних значень ймовірності та кількості вимірювань n.
N |
t′ при рк рівному |
|||
0.05 |
0.02 |
0.01 |
0.005 |
|
2 |
15.56 |
38.97 |
77.96 |
779.7 |
3 |
4.97 |
8.04 |
11.46 |
36.5 |
4 |
3.56 |
5.08 |
6.53 |
14.46 |
5 |
3.04 |
4.10 |
5.04 |
9.43 |
6 |
2.78 |
3.64 |
4.36 |
7.41 |
7 |
2.62 |
3.36 |
3.96 |
6.37 |
8 |
2.51 |
3.18 |
3.71 |
5.73 |
9 |
2.43 |
3.05 |
3.54 |
5.31 |
10 |
2.37 |
2.96 |
3.41 |
5.01 |
11 |
2.33 |
2.89 |
3.31 |
4.79 |
12 |
2.29 |
2.83 |
3.23 |
4.62 |
13 |
2.26 |
2.78 |
3.17 |
4.48 |
14 |
2.24 |
2.74 |
3.12 |
4.37 |
15 |
2.22 |
2.71 |
3.08 |
4.28 |
16 |
2.20 |
2.68 |
3.04 |
4.20 |
17 |
2.18 |
2.66 |
3.01 |
4.13 |
18 |
2.17 |
2.64 |
3.00 |
4.07 |
19 |
2.16 |
2.62 |
2.95 |
4.02 |
20 |
2.145 |
2.60 |
2.93 |
3.98 |
∞ |
1.96 |
2.33 |
2.58 |
3.29 |
Приклад. В додаток до 15-ти вимірювань, результати яких наведено, було виконане 16-те вимірювання, результат якого 772, а відхилення від середнього v16= –27.
: 789; 791;792; 794; 795; 796; 797; 798; 800; 801; 803; 804; 806; 807; 809
= 798.8
СКВ результатів 15 вимірювань
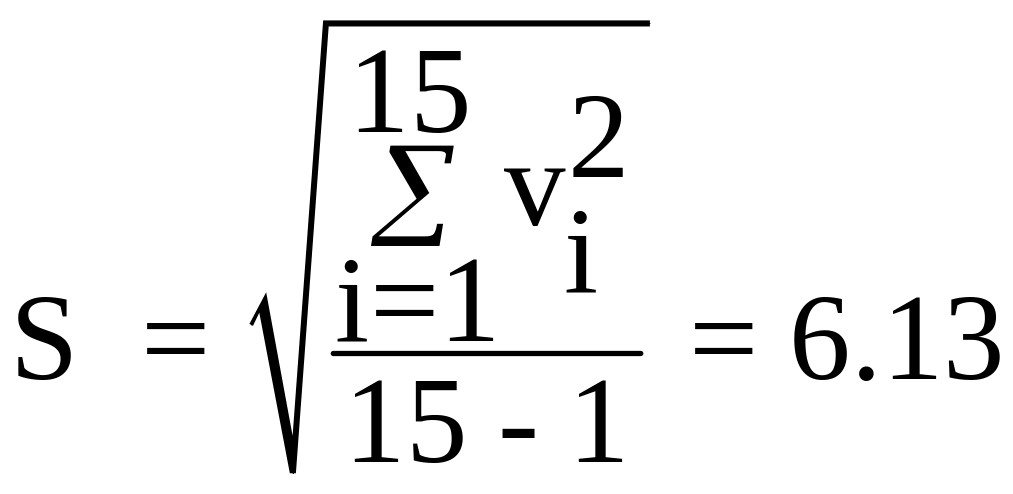
Задамося імовірністю = 0.05 і знаходимо по таблиці для n=15, t′ = 4.28. Звідси
ε*= 4.28 · 6.13 ≈ 26.24.
Результат 16-го вимірювання, для якого v16 = –27 підлягає виключенню із ряду, оскільки 27 > 26.24