7.4. Закон нормального розподілу випадкових величин.

Якщо на основі теоретичних міркувань і досліду можна передбачити якісну форму закону розподілу тієї чи іншої випадкової величини, то буває достатньо виконати невелику кількість вимірювань, щоб повністю визначити його кількісно.

Теоретично було знайдено закони розподілу, які можна очікувати для різних типів випадкових величин. Але для великої кількості випадкових величин, що зустрічаються на практиці, слід очікувати розподілу по так званому закону нормального розподілу (закону Гаусса).

До числа випадкових величин, розподіл яких підлягає цьому закону (або, як іноді кажуть, розподілених нормально), належить більша частина випадкових похибок вимірювання.

7.4.1. Математичний вираз закону нормального розподілу.

Закон нормального розподілу для будь-якої випадкової величини описується рівнянням:

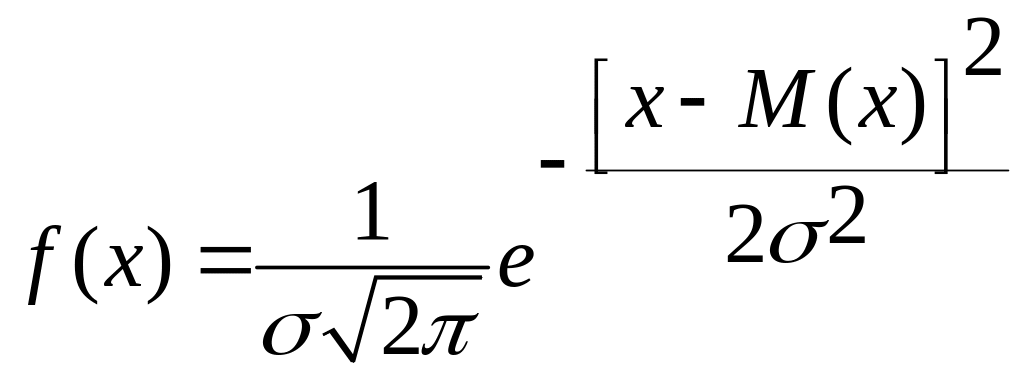(7.24)

де f(х) – густина ймовірності (функція х);

х – значення випадкової величини, для якої визначається f;

М(х) - математичне сподівання (очікування) результатів вимірювань;

σ - середнє квадратичне відхилення результатів вимірювань.

Графік нормального розподілу має вигляд (рис.7.5):

Рис. 7.5. Крива нормального розподілу випадкових величин.

По вісі абсцис відкладено результати спостережень над деякою величиною, яка містить випадкові похибки а по вісі ординат – густина ймовірності їх появи (результатів вимірювань).

При розгляді диференціальної функції розподілу було відзначено. що результати спостережень сконцентровані навколо істинного значення вимірюваної величини, і в міру наближення до нього елементи ймовірності їх виникнення зростають. Це дає право прийняти за оцінку істинного значення вимірюваної величини координату центру тяжіння фігури, утвореної кривою розподілу і віссю абсцис. Ця точка називається математичним сподіванням (очікуванням) результатів спостережень.

Теорія дає наступній висновок: якщо систематичні похибки повністю виключені, то істинне значення вимірюваної величини дорівнює математичному очікуванню результатів спостережень.

Абсциса, яка відповідає математичному очікуванню, називається центром розподілу.

Перенесемо початок координат в центр розподілу, тобто по вісі абсцис будемо відкладати різницю Δ = х – а, де а – істинне значення вимірюваної величини. В результаті отримаємо криву, зображену на рис.7.6.

Рис. 7.6. Крива нормального розподілу випадкових похибок.

Криву (рис.7.6) можна розглядати як криву розподілу випадкових похибок. Її аналітичний вираз має вигляд

. (7.25)

Крива розподілу має дзвоноподібну форму і симетрична відносно осі ординат. Максимальна величина ймовірності дорівнює і досягається у точці 0. По мірі віддалення від точки 0 (вліво чи вправо) ймовірність зменшується і асимптотично наближається до нуля.

7.4.2. Властивості і характеристики нормального розподілу випадкових похибок.

При розгляді властивостей і характеристик розподілу випадкових похибок обмежимося тільки нормальним розподілом, оскільки випадкові похибки вимірювань частіше всього розподіляються нормально.

Будемо розглядати властивості і характеристики нормального розподілу, користуючись його графічним зображенням і рівнянням (7.25).

Властивості нормального розподілу.

1. Найбільша густина ймовірності відповідає похибці Δ =0. При зростанні похибки як в сторону додатніх, так і в сторону від’ємних значень ордината кривої зменшується. Це означає: чим більше похибка Δ, тим менша густина ймовірності її появи, тобто тим рідкіше можна очікувати її появи. При великих Δ крива асимптотично наближаєтьсядо вісі абсцис. Це означає, що густина ймовірності появи дуже великих похибок дуже мала.

2. Крива нормального розподілу симетрична відносно вісі ординат, тобто відносно вертикалі, що проходить через точку Δ = 0. Це означає, що похибки однакові по модулю, але з різними знаками мають однакову густину ймовірності, тобто зустрічаються однаково часто, або, як кажуть, вони рівноімовірні.