3.6. Класифікація засобів вимірювань по точності.

Точність вимірювань – це найважливіша характеристика результатів вимірювань, яка визначає можливість використання отриманих результатів для тих цілей, заради яких вони були виконані.

Одним з вирішальних факторів, які визначають точність вимірювань є точність використованих засобів вимірювань.

Точність засобу вимірювань – характеристика якості засобу вимірювань, яка вказує на близькість його похибки до нуля. Вважається, що, чим менша похибка, тим точніше засіб вимірювань.

Точність засобів вимірювань залежить не тільки від точності їх градуїровки, але і від деяких властивостей, які визначаються наявністю рухомої частини. Однією з причин варіації показів є тертя в опорах рухомої частини приладу.

Точність вимірювальних приладів характеризується сумарною похибкою, тобто похибкою, в яку входить похибка градуїровки і подгонки, а також змінні похибки, варіації та інші. Оскільки змінні похибки змінюються в певних границях, то можна визначити границі сумарних похибок вимірювальних приладів.

Похибки засобів вимірювань, які виявляються при “нормальних” зовнішніх умовах, називаються основними.

За нормальні умови приймають температуру навколишнього середовища t = 20⁰ С, атмосферний тиск 1∙10⁵ Па (760 мм.рт.ст.) і вологість повітря до 80%.

Основна похибка – головна ознака класифікації засобів вимірювань по точності.

Усі засоби вимірювань, крім кутових та довжин, поділяються на класи точності в залежності від значень граничних допустимих похибок.

Під граничною допустимою похибкою розуміють найбільшу з допустимих похибок, або гранична допустима похибка – це похибка, яку не перевищує ні випадкова, ні систематична похибки, ні їх поєднання.

Отже, клас точності засобу вимірюваьної техніки – це узагальнена характеристика, що визначається границями його допустимої основної і додаткової похибок, а також іншими характеристиками, що впливають на його точність, значення яких регламентуються стандартами на окремі види засобів вимірювань.

Клас точності дає можливість зробити висновок про границі похибки засобу вимірювань і відіграє важливу роль при виборі засобів вимірювань.

Наприклад, клас точності нормальних елементів 0,001 свідчить про те, що їх нестабільність за рік не перевищує 0,001%.

Клас точності засобу вимірювань, хоч і характеризує його властивості щодо точності, але не є безпосереднім показником точності вимірювань, які виконані з його допомогою, оскільки точність залежить від методу, умов проведення вимірювань, розмаху шкали приладу та ін.

Класи точності конкретного засобу вимірювань визначаються технічними умовами.

Для кожного виду засобу вимірювань встановлюється ряд класів точності і їм привласнюються різні позначення: номери, числа, літери та інші. Класи точності відповідно до стандарту, як правило, виводяться на шкалу приладів.

Метрологічні характеристики, які визначаються класами точності, нормують наступним чином.

Границі допустимих основної і додаткової похибок виражають у формі приведених, відносних або абсолютних похибок в залежності від характеру зміни похибок, призначення і умов застосування засобів вимірювань.

Якщо похибку результатів вимірювань виражають в одиницях вимірюваної величини (наприклад, при вимірюванні маси, довжини) або в поділках шкали приладу, то границі допустимих похибок виражають в формі абсолютних похибок.

Якщо границі абсолютних похибок засобу вимірювань залишаються практично незмінними, використовують форму приведених похибок.

Якщо границі абсолютних похибок не можна вважати сталими використовують форму відносних похибок.

Різноманітність засобів вимірювань ускладнює можливість єдиного підходу до вибору критерію для їх групування на класи по точності вимірювань.

В основу всіх класифікацій покладено значення гранично допустимої основної похибки: абсолютної, відносної і приведеної. Найбільш обґрунтованою і широко вживаною є класифікація засобів вимірювань не по граничній абсолютній, а по відносній або приведеній основній похибці.

Якщо абсолютна основна похибка ЗВТ не змінюється в межах діапазону вимірювань, то її граничне значення визначають за формулою:

= ± а (3.9),

де - покази засобу вимірювань;

- дійсне значення вимірюваної величини;

а – деяке позитивне число.

Якщо абсолютна основна похибка ЗВТ лінійно змінюється в межах діапазону вимірювань, то її граничне значення визначають за формулою:

(3.10),

де b – деяке позитивне число.

Якщо абсолютна основна похибка ЗВТ має як сталу, так і лінійно змінну компоненти, її граничне значення визначають за формулою:

∆ = ± (a + bх) (3.11),

де х – значення вимірюваної величини на вході або виході засобі вимірювань;

a і b – додатні числа, незалежні від х.

а – адитивна похибка;

bх – мультиплікативна похибка.

Наприклад, для генератора низької частоти ГЗ-36

∆ = ± (0,03f + 2) Гц.

Граничне значення допустимої приведеної основної похибки ( у відсотках) визначають за формулою:

(3.12),

де – нормуюче значення (значення, яке підлягає нормуванню);

р – будь-яке додатнє число з ряду , де n = 1, 0, -1, -2, -3 …

- граничне значення абсолютної похибки визначене за формулою (3.9).

У приладів, для яких адитивна складова похибки переважає над мультиплікативною, основна приведена похибка виявляється сталою в будь-якій точці шкали (діапазону вимірювань), її граничне значення приймається за клас точності засобів вимірювань.

Нормуюче значення залежить від багатьох факторів і приймається рівним:

1. кінцевому значенню шкали приладу, якщо нульова відмітка знаходиться на краю шкали або поза нею;

2. сумі кінцевих значень шкали приладу (без врахування знаків), якщо нульова відмітка знаходиться всередині шкали;

3. номінальному значенню вимірюваної величини, якщо таке встановлено ( наприклад, для частотомірів з діапазоном вимірювання 45-55 Гц і номінальною частотою 50Гц, нормуюче значення = 50 Гц):

4. для вимірювальних приладів з суттєво нерівномірною шкалою приймають рівним всій довжині шкали або її частині, яка відповідає діапазону вимірювань - в цьому випадку похибку і довжину шкали виражають в одних одиницях, наприклад, в одиницях довжини:

5. діапазону вимірювань для багатошкальних приладів, або якщо шкала приладу проградуйована в одиницях величини, для якої прийнята шкала з умовним нулем (наприклад, температура в °С).

В цьому випадку клас точності виражається одним числом з наведеного вище ряду.

Граничне значення основної відносної похибки, виражене в процентах, визначається за формулою:

ε = (3.13),

якщо визначається за виразом (3.10) або за формулою:

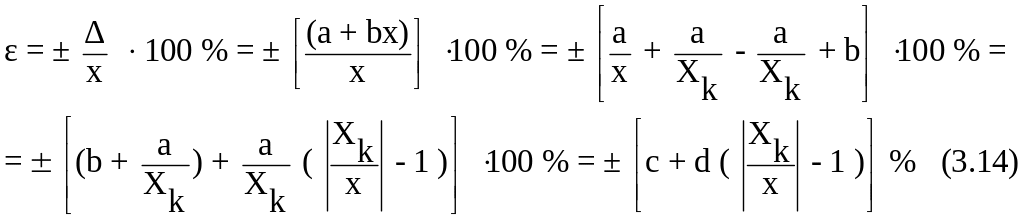
де ∆ - границя допустимої абсолютної основної похибки, що визначається за виразом (3.11);

х – значення вимірюваної величини;