Лекция 5. Основы топологии

Топология, самая юная и самая мощная ветвь геометрии, наглядно демонстрирует плодотворное влияние противоречий между интуицией и логикой

Р. Курант

Топология является одним из самых молодых разделов современной геометрии. Чем занимается топология? Так, например, аналитическая геометрия исследует простейшие геометрические объекты (точки, прямые, плоскости и пр.) средствами элементарной алгебры на основе метода координат. Чтобы получить некоторое представление о топологии, рассмотрим ряд простых и занимательных задач, связанных с ее объектами.

У каждого из нас есть интуитивное представление о том, что такое "поверхность". Поверхность листа бумаги, поверхность стен аудитории, поверхность земного шара известны всем. Возьмите бумажную ленту АВСD, разделенную по ширине пополам пунктирной линией и приложите ее концы АВ и СD друг к другу, склейте их так, чтобы точка А совпала с точкой D, а точка B с точкой С. Перед склейкой перекрутите ленту один раз. Получилось знаменитое в математике бумажное кольцо. Его особое название - "Лист Мёбиуса". У ленты, из которой сделан лист Мёбиуса, две стороны. А у него самого, есть только одна сторона! В качестве опыта, демонстрируемого особенности листа Мебиуса, обычно предлагают «опыт с пауком и мухой». Если на внутреннюю сторону обычного кольца посадить паука, а на наружную - муху и разрешить им ползать как угодно, запретив лишь перелезать через края кольца, то паук никогда не сможет добраться до мухи. А если их обоих посадить на лист Мёбиуса, то бедная муха будет съедена, если, конечно, паук ползает быстрее!

Таинственный и знаменитый лист Мебиуса (иногда говорят: "лента Мёбиуса") придумал в 1858 г. немецкий геометр Август Фердинанд Мёбиус (1790-1868), ученик "короля математиков" Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика была обязана своим развитием. В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мёбиус стал одним из крупнейших геометров XIX в. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей, одна из которых - лист Мёбиуса.

Представленный лист Мебиуса и является объектом изучения новой ветви геометрии – топологии. Топологию часто называют «резиновой геометрией», потому что в ней любую фигуру можно сгибать, скручивать, растягивать, сжимать, но только не разрезать и склеивать. При этом считается, что свойства фигуры остаются неизменными.

При растяжении резинка порвется не сразу, она будет свободно растягиваться, сжиматься, так как эластична. И при таком растяжении или сжатии будут сохраняться все ее особенные свойства – цвет, структура и прочее, при этом изменится только длина и ширина. Поэтому в топологии при рассмотрении объекта не учитывается ни длина, ни величина его углов. Топологические объекты различаются только по «топологической структуре», их свойства могут быть установлены без измерения и сравнения длин и величин углов.

К другим топологическим объектам относятся фигуры, которые можно нарисовать одним росчерком пера. Эти фигуры связаны с топологическим понятием графа. Граф состоит из двух множеств - множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет.

О дной из знаменитых задач, связанных с понятием графов, является задача о Кенигсбергских мостах, называемой еще задачей Эйлера.

В

Задача о Кенигсберских мостах

Кенигсберге есть остров, называемый Кнейпгоф. Река, омывающая его, делится на два рукава, через которые перекинуто семь мостов: а, b, с, d, e, f, g. Можно ли обойти все эти мосты, не побывав ни на одном из них более раза?

Этой задаче Эйлер посвятил целое математическое исследование, которое было в 1736 году представлено в Петербургскую Академию. Для наглядности заменим рисунок расположения речных рукавов упрощенной с хемой (рис.20). В предложенной задаче размер острова и длина мостов никакого значения не имеют (такова характерная особенность всех топологических задач). Задача сводится теперь к тому, чтобы начертить фигуру одним росчерком, не отрывая пера от бумаги и не проводя ни одной линии дважды.

С

Рис.20

начала попытайтесь нарисовать одним росчерком, не отрывая пера от бумаги, не делая никаких лишних штрихов и не проводя дважды ни одной линии, каждую из следующих семи фигур, изображенных на рис. 21. Попытки вычерчивания непрерывной линией фигур 1—7 приводят к неодинаковым результатам. Некоторые фигуры удается вычерчивать, с какой бы точки ни начинать вести первую линию. Другие вычерчиваются одним росчерком в тех лишь случаях, когда начинают с определенных точек. Наконец, третьи вовсе не поддаются вычерчиванию одной непрерывной линией. Существуют ли признаки, позволяющие установить заранее, поддается ли данная фигура вырисовыванию одним росчерком, и если поддается, то с какой точки следует начинать черчение?

Т

Рис.21

еория графов дает на эти вопросы исчерпывающие ответы, и мы сейчас познакомимся с некоторыми положениями этой теории. Условимся называть «четными» те точки фигуры, в которых сходится четное число линий, в отличие от точек «нечетных», в которых встречается   нечетное  число линий. Можно доказать, что какова бы ни была фигура, нечетных точек в ней либо нет совсем, либо их имеется две, четыре, шесть—вообще четное число. В теории графов доказывается, что если нечетных точек в фигуре нет, то она всегда поддается вырисовыванию одним росчерком, безразлично, с какого места ни начинать черчение. Таковы фигуры 1 и 5 . Если в фигуре имеется только одна пара нечетных точек, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных точек (безразлично в какой). Вычерчивание должно оканчиваться во второй нечетной точке. Таковы фигуры 2, 3, 6; в фигуре 6, например, вычерчивание надо начинать либо из точки А, либо из точки В.

Если фигура имеет более одной пары нечетных точек, то она вовсе не может быть нарисована одним росчерком. Таковы фигуры 4 и 7, содержащие по две пары нечетных точек. И теперь уже можно заключить, что и задача Эйлера решений не имеет: по всем семи мостам пройти, как это требуется, невозможно.

Также к «топологической задаче» относится и задача четырёх красок, заключающаяся в доказательстве (или опровержении) следующего предложения: четырёх различных красок достаточно для того, чтобы раскрасить любую карту так, чтобы никакие две области, имеющие общий участок границы, не были окрашены в один и тот же цвет. Доказывается при этом, что пяти красок всегда достаточно для раскраски такого рода "карты". Если же соответствующую задачу формулировать для пространства, то здесь никакое число "красок" не окажется достаточным.

Впервые эта проблема была сформулирована в 1825 году лондонским студентом Гутри, который обнаружил, что для различия графств на карте Англии достаточно четырех красок, и выдвинул гипотезу о том, что четырех красок достаточно для раскраски любой карты. Спустя сорок лет английский математик Хивуд доказал, что любую карту на плоскости можно раскрасить в пять цветов. В дальнейшем проблема четырех красок приобретала все больший и больший интерес. В 1968 году Оре и Стемпл доказали, что любую карту, имеющую не более 40 стран, можно раскрасить в четыре цвета.

В настоящее время проблема четырех красок решена с помощью компьютерной визуализации. Учеными с помощью компьютера было просмотрено около 2000 типов карт и был получен вывод, что не существует среди них карты, для раскраски которой недостаточно четырех красок. Однако, поскольку нельзя признать, что все типы карт были рассмотрены, то полученное решение окончательным не считается и в настоящее время проблема четырех красок остается открытой.

В топологии существуют и свои объекты, и свои свойства, отличающиеся от свойств фигур в евклидовой геометрии.

Топологическим свойством геометрических фигур называется свойство, которым вместе с данной фигурой обладает также любая фигура, в которую она переходит при топологическом преобразовании. Проще говоря, если из одной фигуры можно получить другую, без разрывов и склеиваний, то эти две фигуры являются топологически одинаковыми и обладают одинаковыми топологическими свойствами.

Окружность с помощью деформации можно преобразовать в овал, в треугольник, в квадрат, вообще в произвольный многоугольник без самопересечении, в произвольную замкнутую кривую без самопересечений, что позволяет нам судить о топологической эквивалентности (или, как еще говорят, гомеоморфности) всех вышеперечисленных фигур (рис.22).

П

Рис.22

о определению все топологические свойства у гомеоморфных фигур совпадают, поэтому для топологии, изучающей лишь топологические свойства, все гомеоморфные между собой фигуры представляют как бы различные экземпляры одного и того же топологического образа, как, например, все конгруэнтные между собой треугольники в школьном курсе геометрии.

В связи с этим и вводится понятие топологического типа. Для того, чтобы две фигуры принадлежали одному и тому же топологическому типу, необходимо и достаточно, чтобы они были гомеоморфными.

Так, рассмотренные выше фигуры принадлежат одному топологическому типу; отрезок, дуга, незамкнутая ломаная - другому; «восьмерка» не принадлежит ни одному из этих типов. Сфера, куб, выпуклый многогранник образуют свой топологический тип и т. д.

Возьмем лист бумаги. Согните его, как угодно, сделайте из него самолетик, кораблик, сомнем его в комок. Если в результате этих преобразований он нигде не порвался, то во всех этих состояниях все его виды – кораблик, самолетик, комок, эквивалентны друг другу. Более того, если допустить, что лист бумаги обладает особыми свойствами, позволяющими его растягивать как угодно и сжимать до любой степени, то он будет эквивалентен даже кругу. Если же все- таки случайно он порвался и образовалось отверстие, то это будет другая поверхность, называемая кольцом. Говорят, что она ограничена двумя окружностями

К особым топологическим свойствам относятся: связность, компактность, линейная связность.

Понятие связности обобщает интуитивное представление о целостности, неразделенности геометрической фигуры, а понятие несвязного пространства – отрицание целостности, разделенность.

Пространство X называется несвязным, если его можно представить как объединение двух непустых непересекающихся множеств. В противном случае пространство называется связным. Простейшими примерами связного множества служит отрезок [a, b] числовой оси R, несвязного – гипербола, если вспомнить, что собой представляет график гиперболы – две обособленные бесконечные ветви.

Т

Памятник Мебиусу

опологическое пространство называется отделимым, если у любых его различных точек существуют непересекающиеся окрестности. Например, отделимыми являются числовое пространство, евклидово пространство, все метрические, аффинное и проективное пространства, потому что для каждых двух точек можно выбрать такие окрестности, чтобы они не имели общих точек.

Компактные объекты – это объекты, которые одновременно и ограничены (например, вокруг них можно описать окружность или сферу), и замкнуты (то есть граничные точки принадлежат объекту).

К

Тор

акие же топологические объекты можно перечислить? Простейшая замкнутая поверхность, это, конечно, сфера. Второй интересный топологический объект – это тор, или как еще иначе его называют, бублик, баранка – по форме он действительно напоминает всеми любимое мучное изделие.

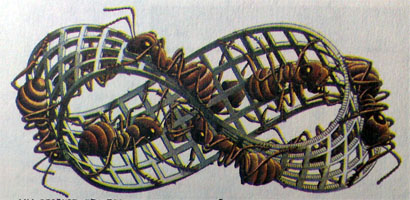
Следующий объект – это уже известный лист Мебиуса.

Лист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса II, показывает муравьёв, ползающих по поверхности ленты Мёбиуса. Муравьи Эшера демонстрируют свойства листа Мёбиуса: муравьи ползут по одной стороне листа, но кажется, будто они движутся по противоположным его сторонам. Лист, дважды перекрученный на пол-оборота, имеет две стороны. Число перекручиваний определяет число сторон и приводит к неожиданным эффектам при разрезании листа Мёбиуса вдоль оси.

Муравьи Эшера

Лист Мёбиуса был эмблемой известной серии научно-популярных книг «Библиотечка „Квант“». Он также постоянно встречается в научной фантастике, например в рассказе Артура Кларка «Стена Темноты». В рассказе «Лист Мёбиуса» автора А. Дж. Дейча, бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда. По мотивам рассказа был снят фантастический фильм «Мёбиус» режиссёра Густаво Москера. Также идея ленты Мёбиуса используется в рассказе М. Клифтона «На ленте Мёбиуса».

С лентой Мёбиуса сравнивается течение романа современного русского писателя Алексея А. Шепелёва «Echo» (СПб.: Амфора, 2003). Из аннотации к книге: «„Echo“ — литературная аналогия кольца Мёбиуса: две сюжетные линии — „мальчиков“ и „девочек“ — переплетаются, перетекают друг в друга, но не пересекаются».

Еще один объект топологии - бутылка Клейна.

Феликс Клейн - это математик, который первым исследовал эту поверхность, а вот почему "бутылка"? Ведь на бутылку это мало похоже. Вероятно, после какой-то деформации сходство с бутылкой становится ближе?

Если муха захочет переползти с наружной поверхности обычной бутылки на внутреннюю или наоборот, ей непременно придется пересечь край, образуемый горлышком. В отличие от обычной бутылки бутылка Клейна не имеет края, а ее поверхность нельзя разделить на внутреннюю и наружную. Та поверхность, которая кажется наружной, непрерывно переходит в ту, которая кажется внутренней, как переходят друг в друга две, на первый взгляд различные, "стороны" листа Мебиуса. К сожалению, в трехмерном пространстве бутылку Клейна фактически реализовать сложно и невозможно, но в топологии изучаются не то, что возможно или нет, а просто какие возможны комбинации.

Представим себе, что мы оттянули нижний конец трубки, загнули его вверх и, пропустив сквозь поверхность трубки, совместили с верхним концом. У реальной модели, изготовленной, например, из стекла, в том месте, где конец трубки проходит сквозь ее поверхность, придется оставить отверстие. Его не следует принимать во внимание: оно считается как бы затянутым продолжением поверхности бутылки. Иначе говоря, отверстия нет, есть только самопересечение поверхности бутылки. Такое самопересечение неизбежно до тех пор, пока мы имеем дело с трехмерной моделью. Если же мы представим себе, что вся поверхность погружена в четырехмерное пространство, то самопересечение можно будет полностью исключить.

Известный специалист по алгебраической геометрии Д. Пидо написал книгу под названием "Прекрасное искусство математики". Это великолепная книга, однако профессор Пидо, следуя установившейся традиции, допускает там неверное утверждение. Он пишет, что изготовить бутылку Клейна под силу лишь искусному стеклодуву, сделать же бутылку Клейна "из бумаги совсем невозможно". Действительно, в то время, когда профессор Пидо писал свою книгу, никто даже не пытался склеить бумажную модель бутылки Клейна. Но так продолжалось лишь до тех пор, пока за дело не взялся Стифен Барр, писатель-фантаст, а на досуге — большой любитель занимательной математики.

Барр довольно быстро придумал множество способов складывания из бумаги моделей бутылки Клейна и даже написал книгу о топологических развлечениях. В книге Барра приводится множество новых способов, п озволяющих складывать из обыкновенного листа бумаги изящные топологические модели.

Б

Бутылка Клейна

утылка Клейна является замкнутой односторонней поверхностью, если налить в такую бутылку воду, то вылить ее обратно уже будет совершенно невозможно.

Итак, топология – это особый раздел геометрии, в котором нет места понятиям расстояние, форма, угол. Линия не бывает здесь прямой или кривой - это просто линия. Поверхность не может быть вогнутой или выпуклой, или плоской - это бессмысленные для топологии слова. Но, например, отрезок и замкнутую линию - это топологически разные объекты. Объекты топологии бывают односторонние и двусторонние. Например, куб - двусторонняя поверхность, лист Мебиуса –односторонняя.

Но этот, казалось бы, странный раздел математики тесно связан с реальным миром. Например, электрическая цепь – понятие топологическое, поскольку существенно не расположение ее элементов в пространстве, а связи между ними. Топология графов (раздел топологии, занимающийся изучением сетей) имеет первостепенное значение при проектировании сложных электрических цепей. С топологией мы сталкиваемся в ткацком деле и вязании. Заузленная петля остается заузленной («не развязывается») при любых деформациях. Топологически она отличается от незаузленной петли. Текстильщики упражняются в топологии, пытаясь создать ткани с особыми топологическими свойствами, которые, например, можно связать целиком из одной нити или которые не «ползут» при обрыве одной нити: чтобы ткань при обрыве волокна не «поползла», разработана сложная система узлов и переплетений.

Существуют и технические применения ленты Мёбиуса. Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому что вся поверхность ленты изнашивается равномерно. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи). Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.

Линии на карте-схеме Московского метрополитена сильно искажены по сравнению с реальными путями. Тем не менее, каждой точке путей соответствует точка на схеме, и любые две точки, соединенные на карте, соединены в действительности: схема и лондонская «подземка» топологически эквивалентны.

Но настоящая топология – пока еще не нашла широкого применения на практике (ни один из ее разделов не связан с производственной деятельностью так тесно, как, например, арифметика с банковским делом) и по-прежнему остается «площадкой для игр» теоретиков, теоремы топологии, хотя они и доказаны вполне строго, не находят столь прямых приложений, как, например, теоремы геометрии.