1.3. Показатели надежности возведенных конструкций

Параметр _i в формуле r = 1/ П_I определяется на множестве {_ij} показателей надежности возведенных однотипных конструкций в i - ой группе конструкций несущего каркаса объекта. Показателем надежности возведенной конструкции может служить либо вероятность безотказного ее функционирования (термин теории надежности), либо степень принадлежности конструкции к множеству аналогичных конструкций, но в которых все требованиям проекта выполнены (термин теории множеств). В рамках классической теории надежности задача определения показателей {_ij} требует значительных затрат времени. Поэтому в «on-line» технологиях методы теории надежности практически не находят применения. Для решения таких задач следует использовать методы теории нечётких (размытых) множеств.

В классической (четкой) теории множеств принадлежность элементов к тому или иному множеству оценивается в соответствии с чётким условием – элемент либо принадлежит, либо не принадлежит данному множеству. Теория нечётких множеств разрешает градуированную оценку отношения принадлежности элементов основному множеству, и это отношение описывается при помощи функции принадлежности, которая на некотором множестве может действовать так же, как индикаторная функция, отображая все элементы либо в 1, либо в 0, как в классическом варианте.

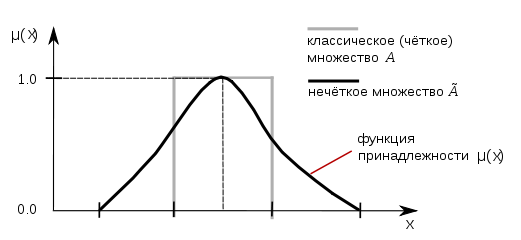Функция принадлежности µ количественно градуирует принадлежность элементов нечёткому множеству. Значение 0 означает, что элемент не включен в нечёткое множество, 1 – описывает полностью включенный элемент. Значения между 0 и 1 характеризуют нечётко включенные элементы (рис.1). В теории нечетких множеств используется лингвистическая переменная. Она отличается от числовой переменной тем, что ее значениями являются не числа, а слова - модификаторы (очень, вполне и т.д.).

Рис. 1 Нечёткое множество и классическое, четкое (crisp) множество.

В инженерно-экспертной практике надежность поврежденной конструкции почти всегда оценивается через соответствие ее параметров требованиям нормативных документов, в частности, проекта. В нечеткой логики понятия надежность, степень принадлежности и соответствие отождествляются, но степень соответствия при этом изменяется в пределах не от 1 до 0, а от 1 до 0,5. Доказательством служит человеческий опыт, измеряющий соответствие голосованием (выборы, суды присяжных и т.д.), где мерой предельного соответствия является величина 0,5.

Для назначения показателей надежности возведенных на объекте конструкций можно воспользоваться правилом (табл.1), построенном на приемах нечеткой логики с применением лингвистической переменной «очень» [19]. С этой целью введено понятие ранг опасности конструкции и к каждому рангу назначен лингвистический терм в виде отношения конструкции к требованиям проекта в части обеспечения ее прочности, жесткости и устойчивости. Правило содержит 10-ть рангов опасности конструкции, различающихся по показателю степени переменной «очень».

Таблица 1

Правило назначения показателя надежности конструкции

Отношение конструкции к требованиям проекта	Ранг опасности	Степень переменной «очень»	Показатель надежности конструкции
Соответствие требованиям проекта практически полное	1.1	(очень)0,01	0,994
	1.2	(очень)0,02	0,987
	1.3	(очень)0,03	0,981
Отклонения от требований проекта незначительные	2.1	(очень)0,05	0,969
	2.2	(очень)0,10	0,939
	2.3	(очень)0,15	0,910
Отклонения от требований проекта значительные	3.1	(очень)0,20	0,882
	3.2	(очень)0,30	0,828
	3.3	(очень)0,40	0,777
Соответствие требованиям проекта низкое	4.1	(очень)0,50	0,730
	4.2	(очень)0,60	0,686
	4.3	(очень)0,70	0,644
Соответствия требованиям проекта практически нет	5.1	(очень)0,80	0,604
	5.2	(очень)0,90	0,568
	5.3	(очень)1,00	0,533
Соответствие предельно-низкое	6	(очень)1,10	0,500
Конструкция содержит опасный дефект	7.1	(очень)1,20	0,470
	7.2	(очень)1,30	0,441
	7.3	(очень)1,40	0,414
Конструкция содержит несколько опасных дефектов	8.1	(очень)1,50	0,389
	8.2	(очень)1,60	0,365
	8.3	(очень)1,70	0,343
Конструкция содержит угрожающие аварией дефекты	9.1	(очень)1,80	0,322
	9.2	(очень)1,90	0,303
	9.3	(очень)2,00	0,284
Состояние конструкции практически предельное	10	(очень)2,20	0,250

При построении этого правила использован прием нечеткой логики, состоящий в отождествлении понятий «надежность» и «соответствие». Поскольку мера соответствия в отличие от меры надежности изменяется от 1 до 0,5, показатели надежности в табл. 1 разделены на две части, одна из которых содержит степени соответствия, другая – несоответствия. Границей между частями является шестой уровень опасности, характеризуемый предельно низкой степенью соответствия требованиям проекта, равной 0,5. Этот факт дал возможность лингвистической переменной (очень)^1,10 шестого уровня опасности присвоить меру предельного соответствия, равную 0,5. Это в свою очередь позволило получить числовую оценку лингвистической переменной «очень» и вычислить числовую меру надежности для остальных 9-и рангов опасности, представленных в табл. 1.

Таблица является рабочим инструментом эксперта. Эксперту для назначения показателя надежности элементов множества {_{i j}} достаточно по их состоянию и на основе своих знаний и опыта установить ранг опасности возведенной на объекте конструкции. При этом назначенный по таблице показатель надежности элемента множества будет иметь погрешность, не превышающую размеров примыкающих интервалов, поскольку выход за их пределы практически невозможен.

Для повышения точности и достоверности экспертных решений по оценке показателей надежности дефектных конструкций можно использовать прием, когда в процедуре назначения рангов их опасности участвуют несколько экспертов при условии, что их опыт и знания сопоставимы, а окончательное решение принимается коллегиально.

Оценка показателей надежности по численной информации о техническом состоянии дефектной конструкции, предоставляемой экспертом, по существу является процедурой формализации этой информации, то есть переводом ее в безразмерный вид. Полученное здесь правило для назначения показателей надежности конструкций совпадает с правилом, полученным автором работы [39] на основе функции принадлежности, предложенной американским математиком Лотфи А. Заде.