6. Плоскости и прямые в пространстве

Пример. Даны координаты вершин пирамиды

А₁(1,-2,-3), А₂(-3,1,1), А₃(4,3,-1), А₄(3,2,2).

Составить: 1. Уравнение плоскости , 2. Уравнение перпендикуляра, опущенного из вершины А₄ на грань .

Решение. 1. Уравнение плоскости запишем, используя каноническое уравнение плоскости, проходящей через три данные точки:

.

Подставив координаты точек А₁, А₂, А₃, получим

= .

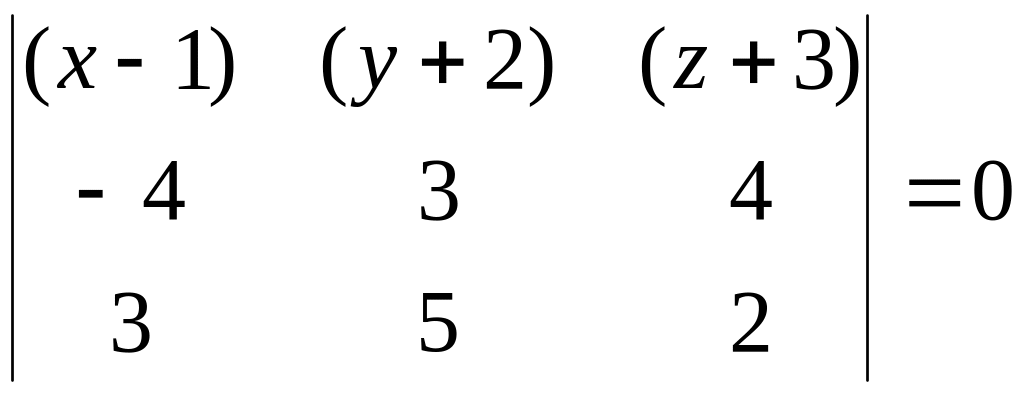Разложив последний определитель по элементам первой строки, будем иметь

или

.

2. Уравнение высоты пирамиды представим в виде канонической системы уравнений прямой, проходящей через заданную точку А₄ с известным направляющим вектором . За направляющий вектор возьмем нормальный вектор плоскости , т.е. .

Уравнение высоты: .

Примечание. Если бы в уравнении прямой один из знаменателей оказался нулевым, например

,

то уравнение прямой следовало бы записать в виде пересекающейся системы плоскостей

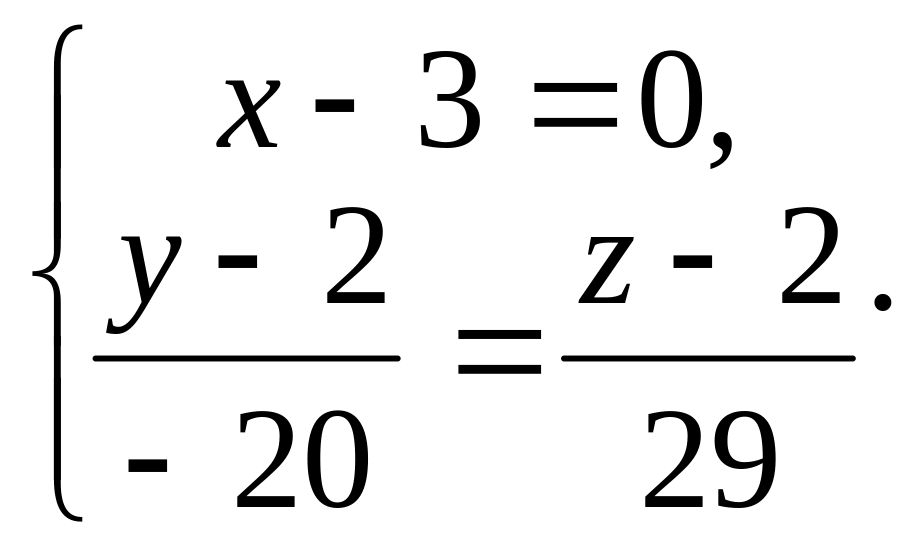
Наконец, если бы в уравнении прямой два знаменателя обратились в ноль, например,

,

это означало бы, что прямая является пересечением плоскостей и и ее уравнением будет система

7. Линии второго порядка

1, гл. III, § 1, 2.

2, упр. 385, 397, 398, 444, 472, 509, 512, 515, 516, 522, 526, 530, 532, 541, 542, 585, 588, 591, 599, 600, 607.

3, гл. VI, § 1-3; § 4, п.2.

4, гл. I, § 8-11.

Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С(x₀, y₀) (случай В).

А В

Окружность
Эллипс
Гипербола
Парабола

Пример. Найти геометрическое место точек разность квадратов расстояний которых от точек А(1, 2) и В(5, 3) равна 4.

Решение. Обозначим за М(x, y) текущую точку кривой. Тогда по условию МА – МВ = 4. В координатной форме

, или

.

Перенесем второй корень направо и возведем в квадрат

или . Это уравнение прямой линии (рис. 3)

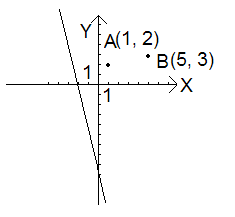
Рис. 3.

Контрольная работа 1. Задания.

1. Решить систему методами Гаусса и Крамера

1.1.	.	1.11.	.
1.2	.	1.12.	.
1.3.	.	1.13.	.
1.4.	.	1.14.	.
1.5.	.	1.15.	.
1.6.	.	1.16.	.
1.7.	.	1.17.	.
1.8.	.	1.18.	.
19.	.	1.19.	.
1.10.	.	1.20.	.

2. Даны координаты вершин пирамиды . Средствами векторной алгебры найти:

1) длину ребра ;

2) угол между ребрами и ;

3) уравнение плоскости ;

4) уравнение перпендикуляра, опущенного из вершины на грань ;

5) площадь грани ;

6) объем пирамиды.

2.1.	,	,	,	.
2.2.	,	,	,	.
2.3.	,	,	,	.
2.4.	,	,	,	.
2.5.	,	,	,	.
2.6.	,	,	,	.
2.7.	,	,	,	.
2.8.	,	,	,	.
2.9.	,	,	,	.
2.10.	,	,	,
2.11.	,	,	,	.
2.12.	,	,	,	.
2.13.	,	,	,	.
2.14.	,	,	,	.
2.15.	,	,	,	.
2.16.	,	,	,	.
2.17.	,	,	,	.
2.18.	,	,	,	.
2.19.	,	,	,	.
2.20.	,	,	,	.

В задачах 3.1 – 20 по аналитической геометрии сде­лать чертеж.

3. Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС, угол между ними, уравнения медианы СК и высоты АМ. Сделать чертеж

№	А	В	С	№	А	В	С
3.1.	(-5, 3)	(10,6)	(1, 5)	3.11	(14, 5)	(4, 5)	(-5,-8)
3.2.	(-7, 1)	(5, 0)	(2, 5)	3.12	(10, 2)	(2, 0)	(5, -2)
3.3.	(5, 1)	(0, 3)	(-2, 4)	3.13	(0, -2)	(-2, 1)	(3, 1)
3.4.	(5, 2)	(-1, 0)	(4, 4)	3.14	(-1, 2)	(1, -1)	(-5, 1)
3.5.	(2, -2)	(3, -4)	(2, -1)	3.15	(4, 8)	(-3, 3)	(7, 5)
3.6.				3.16	(4, 4)	(5, 2)	(-1, 0)
3.7.				3.17	(-2, 4)	(5, 1)	(0, 3)
3.8.	(-2, 1)	(3, 1)	(0, -2)	3.18
3.9.	(-3, 3)	(7, 5)	(4, 8)	3.19	(1, 5)	(-5, 3)	(10,6)
3.10	(2, 0)	(5, -2)	(10, 2)	3.20

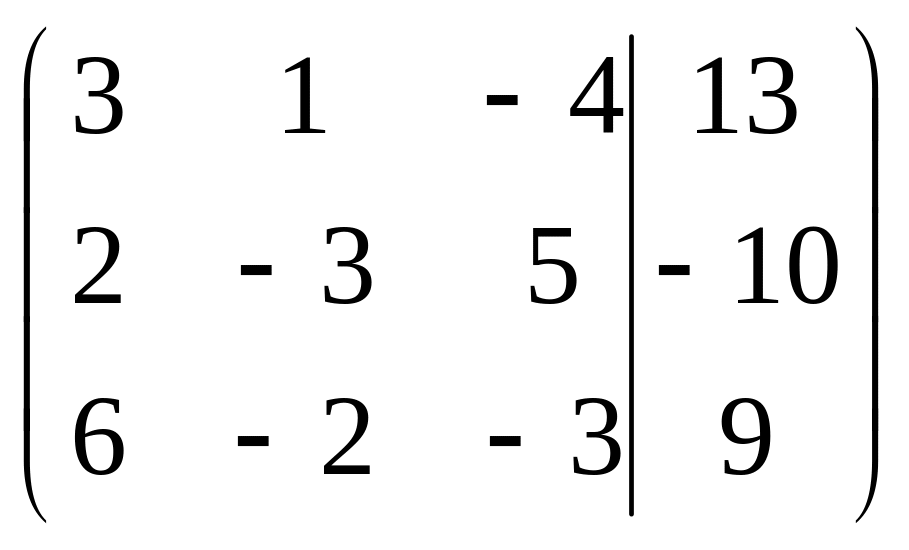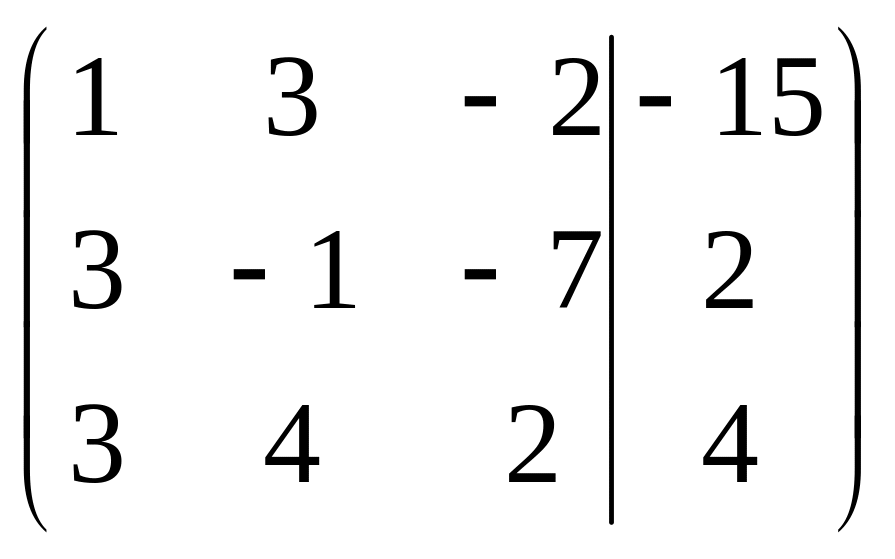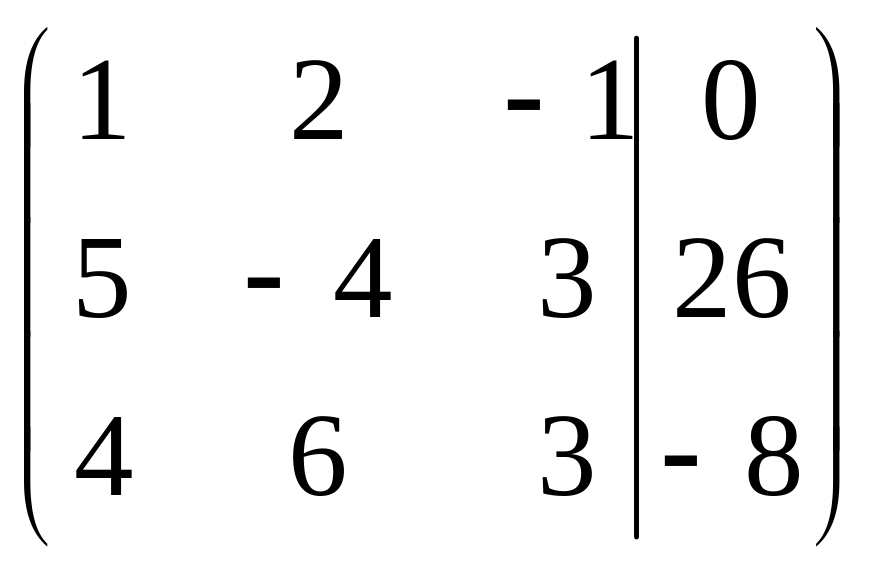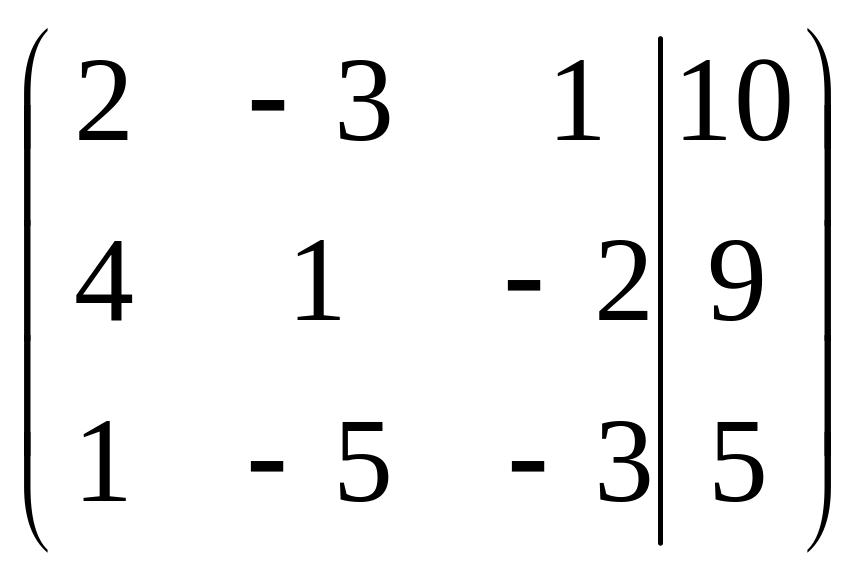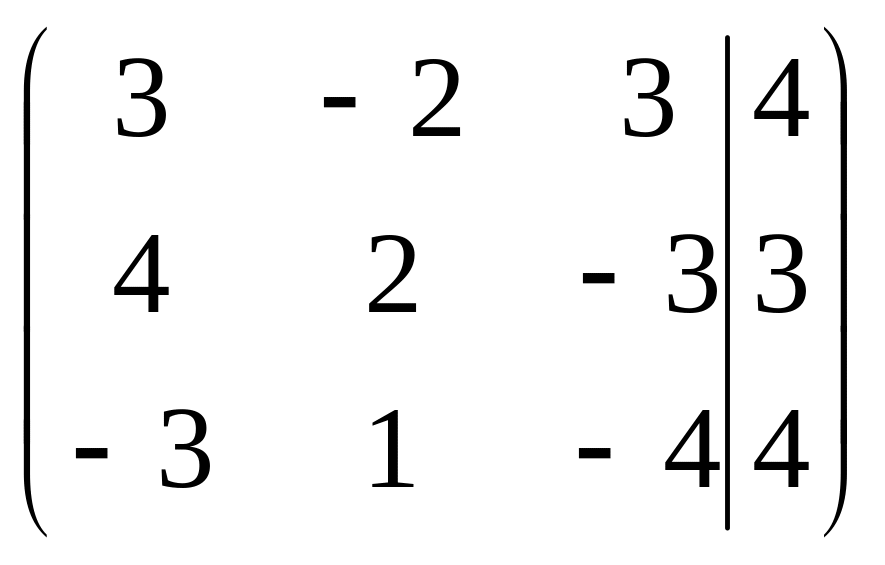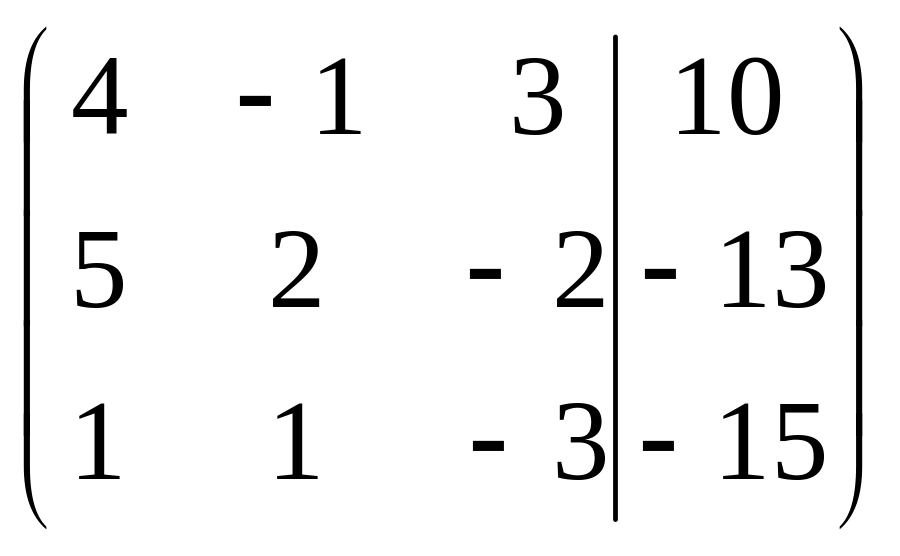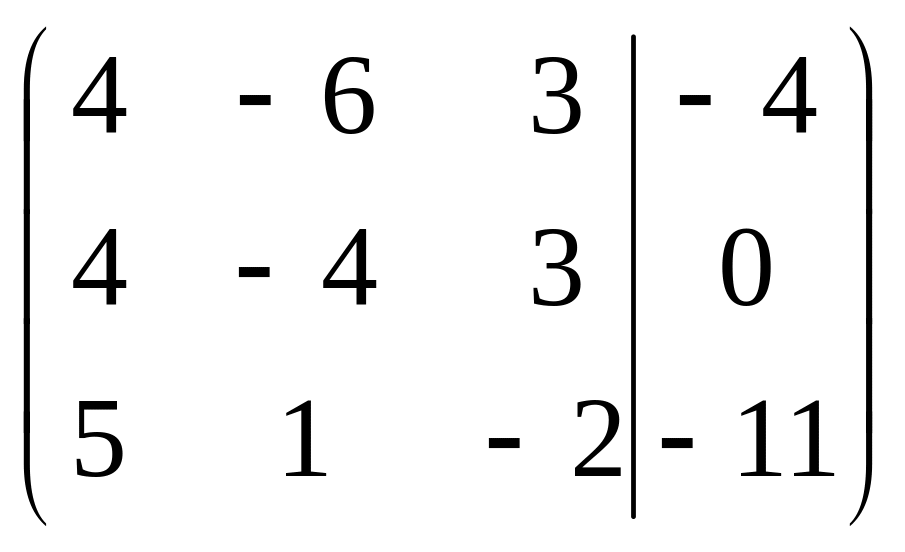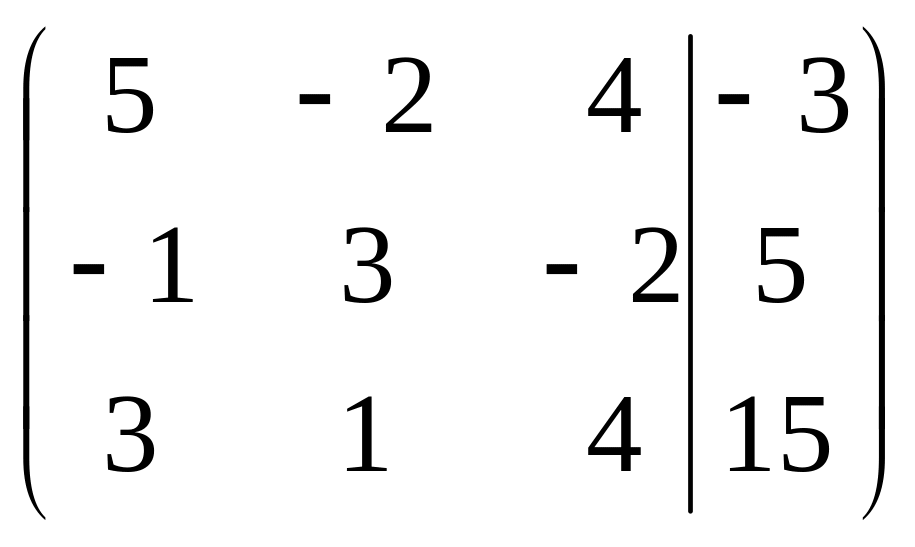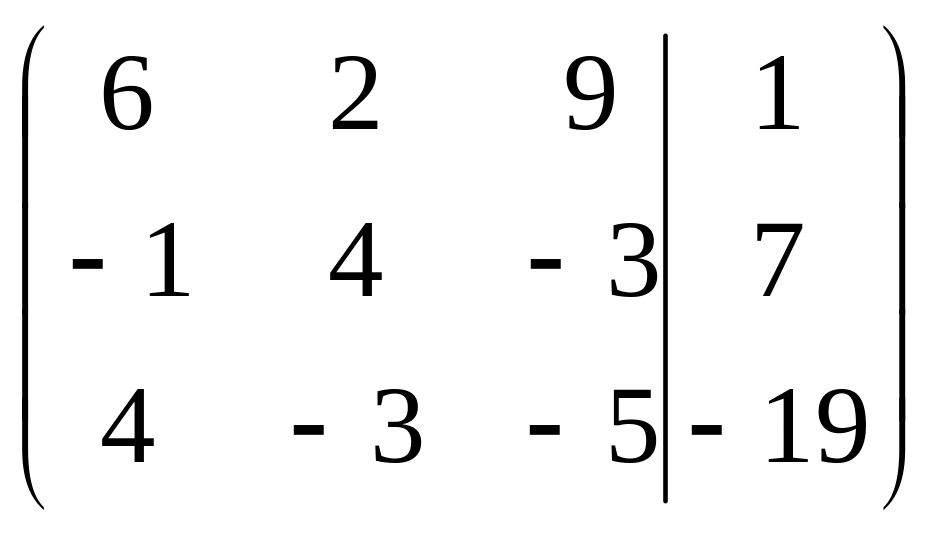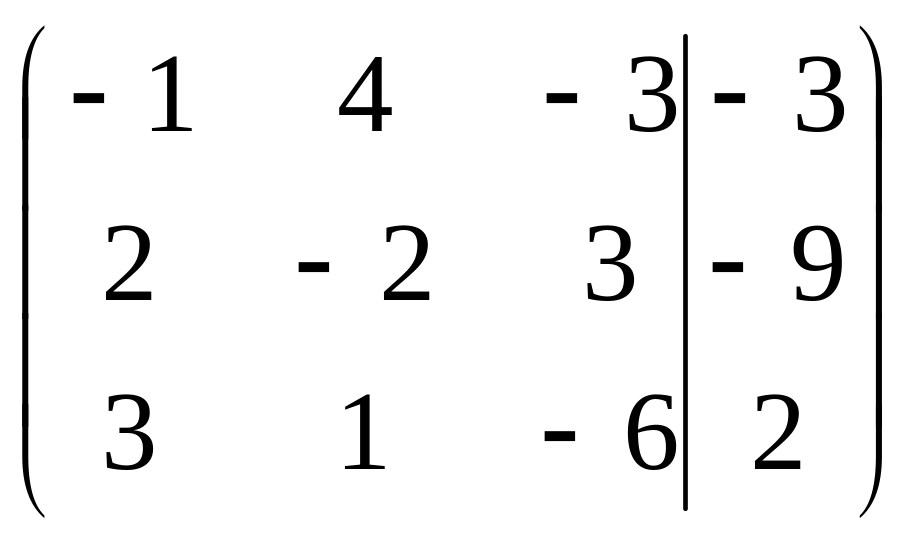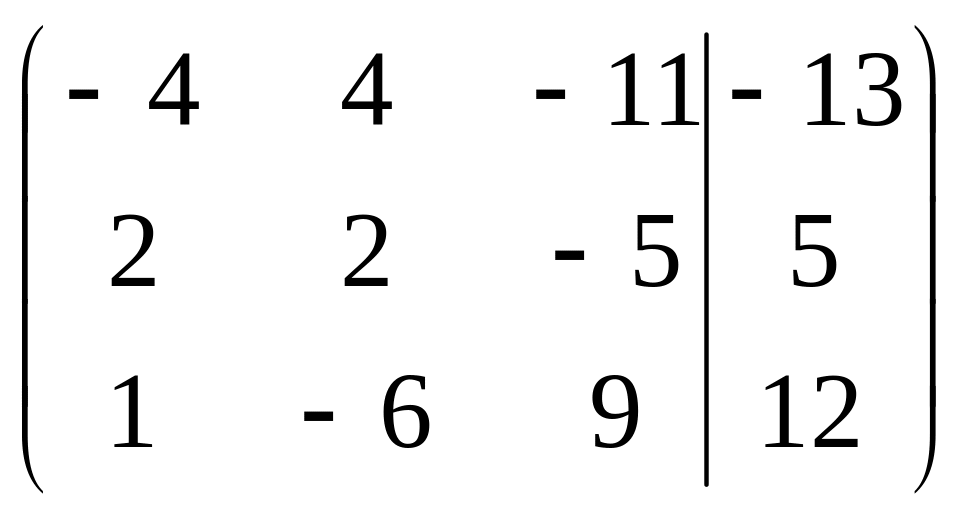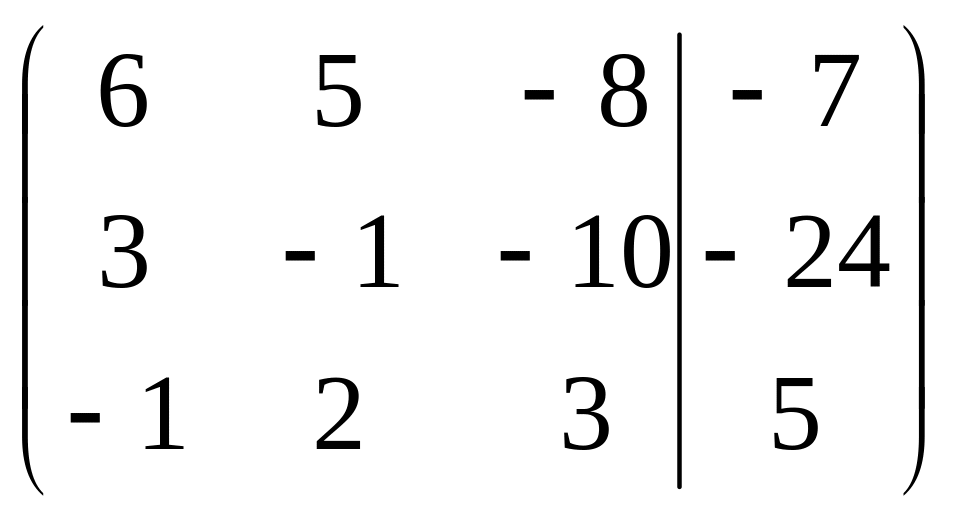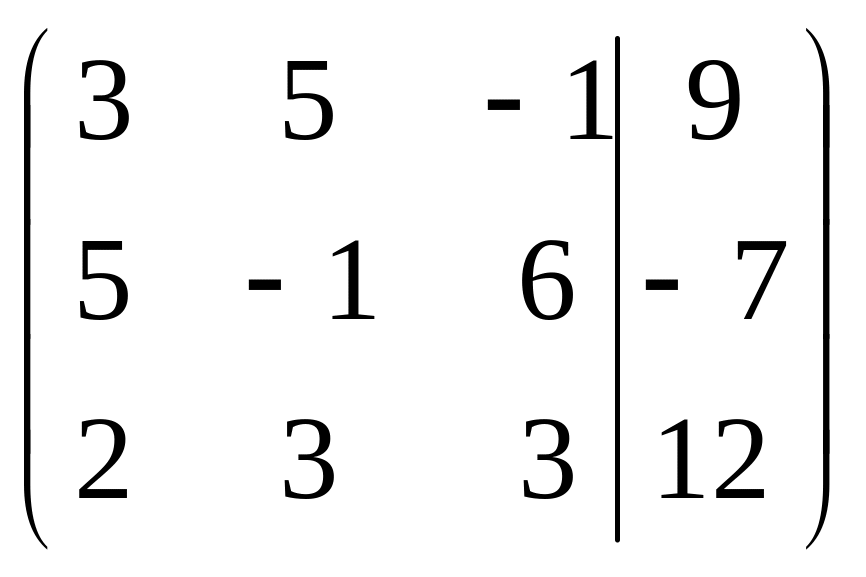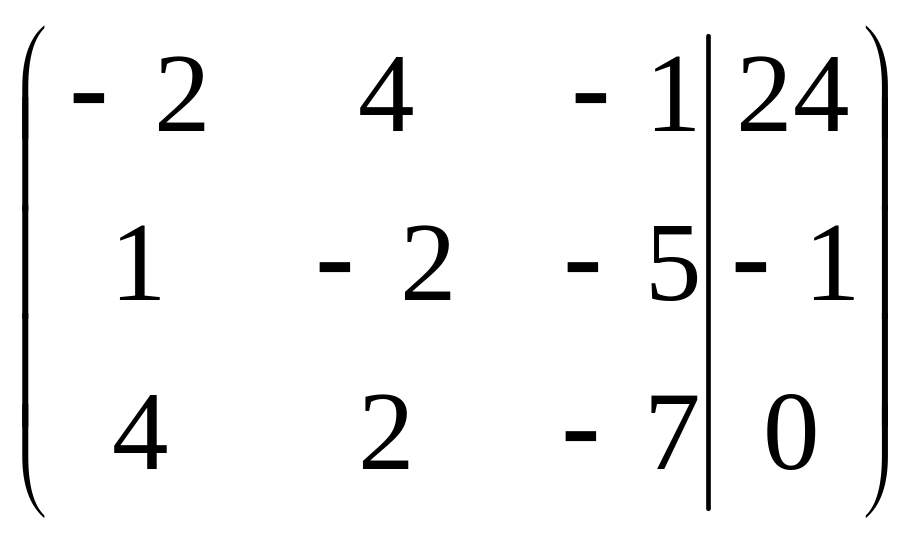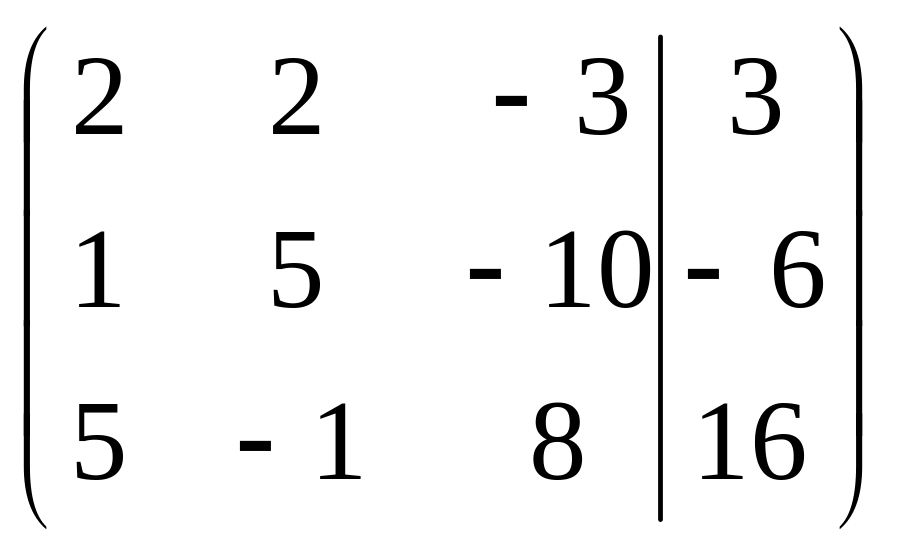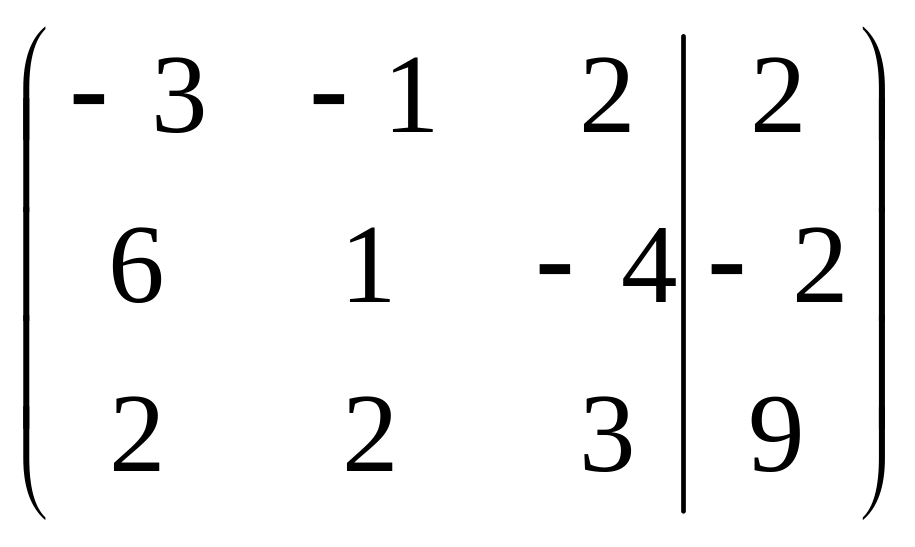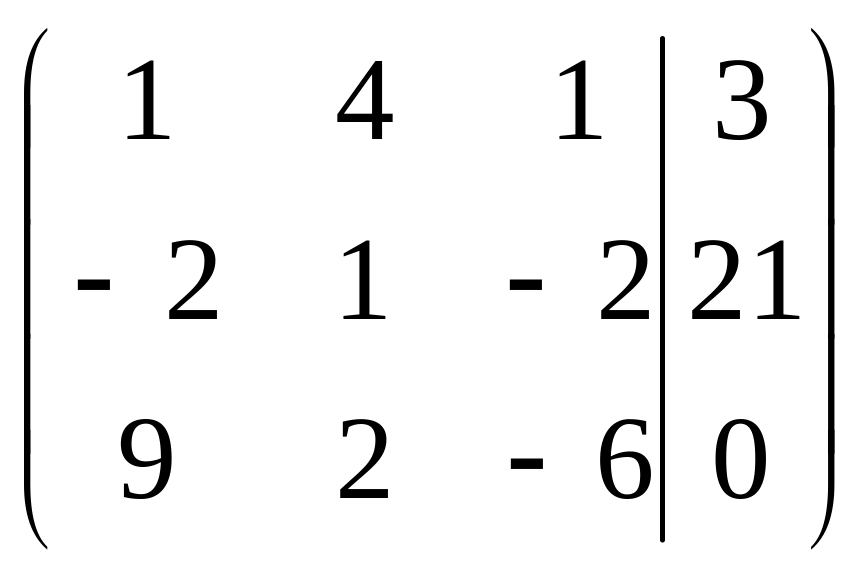14