6.2.2 Свойства средней арифметической
Первое свойство. Сумма отклонений значений признака Х от средней арифметической х равна нулю:
∑(х
–
)
= 0.
∑(х – ) = ∑х – ∑ = ∑х – n .
Из
формулы средней арифметической
невзвешенной
следует, что ∑х
= nх.
Следовательно,
∑(х – ) = 0.
Все свойства средней арифметической позволяют во многих случаях упростить ее расчеты: можно из всех значений признака вычесть произвольную постоянную величину, разность сократить на общий множитель, а затем исчисленную среднюю умножить на общий множитель и прибавить произвольную постоянную величину.
Формула средней арифметической взвешенной получит следующий вид:
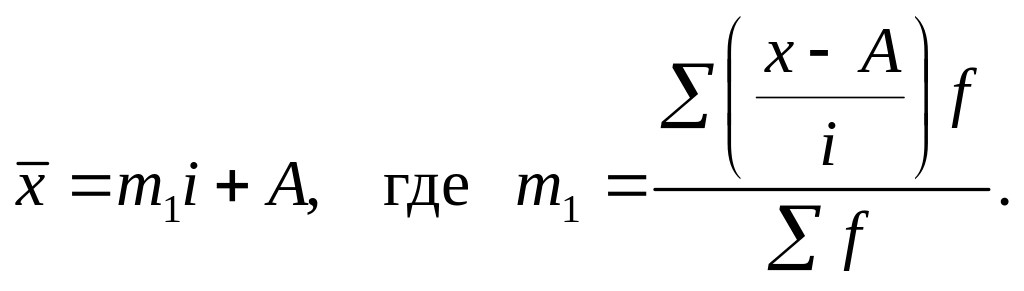
Средняя m1 из значения х–А/i называется моментом первого порядка, а способ вычисления средней – способом моментов. Иногда его также называют способом отсчета от условного нуля.
Второе свойство. Если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число:
.
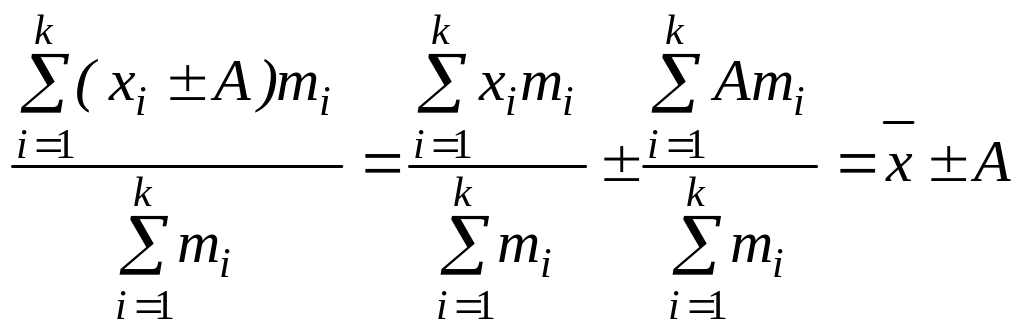Пример. Пусть заработная плата каждого работника фирмы «Весна» увеличилась за некоторый период на 15000 д. е. Тогда средняя заработная плата всех работников фирмы увеличилась также на 15000 д. е.
Третье свойство. Если все варианты одинаково увеличить (или уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (или уменьшится) во столько же раз:
.
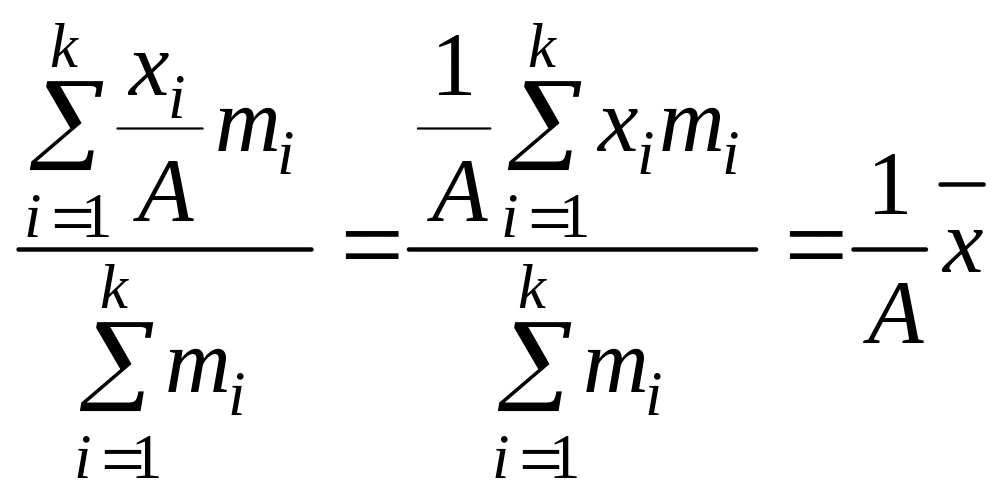Пример. Так, если бы заработная плата каждого работника фирмы «Весна» увеличилась на 10 %, то и средняя заработная плата всех работников фирмы увеличилась бы на 10 %.
Четвертое свойство. Если же все веса средней одинаково увеличить (или уменьшить) в несколько раз, средняя арифметическая не изменится. Увеличение всех весов в несколько раз приводит к тому, что во столько же одновременно увеличится и числитель, и знаменатель дроби (средней арифметической), поэтому значение дроби не изменяется.
6.2.3 Средняя гармоническая
Средняя гармоническая применяется в тех случаях, когда частоты (веса) не приводятся непосредственно, а входят сомножителями в один из имеющихся показателей
Пример. Автомобиль доставил товары в три магазина фирмы «Весна», которые удалены от головного предприятия на одинаковое расстояние. Так, до первого магазина, расположенного на шоссейной дороге, автомобиль прошел путь со скоростью 50 км/ч; до второго по проселочной дороге – 40 км/ч; в третьем случае автомобилю пришлось полпути пройти через лесной массив, и скорость движения составила только 30 км/ч.
Требуется определить среднюю скорость движения автомобиля. На первый взгляд представляется, что средняя скорость движения может быть определена по формуле простой арифметической:
Однако нетрудно убедиться, что средняя вычислена неправильно. В самом деле, производя расчет средней скорости по простой арифметической средней, исходим из того, что автомобиль во всех трех случаях прошел одинаковое расстояние, пройдя соответственно 50, 40 и 30 км, т. е. всего 120 км. Если бы условие этой задачи было сформулировано в такой форме, то средняя была бы рассчитана правильно и характеризовала бы пройденное автомобилем среднее расстояние.
В действительности же эта средняя рассчитана неверно, так как из условия задачи не следует, что автомобиль на преодоление расстояния до трех магазинов фирмы «Весна» проехал 120 км, так как скорость движения была различная. Следовательно, он прошел и разное расстояние.
В подобных случаях нужно применить формулу средней гармонической простой (не взвешенной)
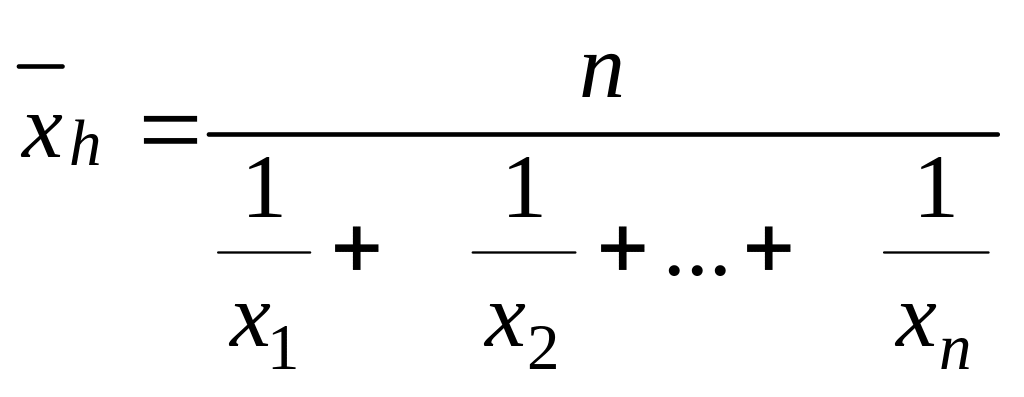
или в сокращенном виде
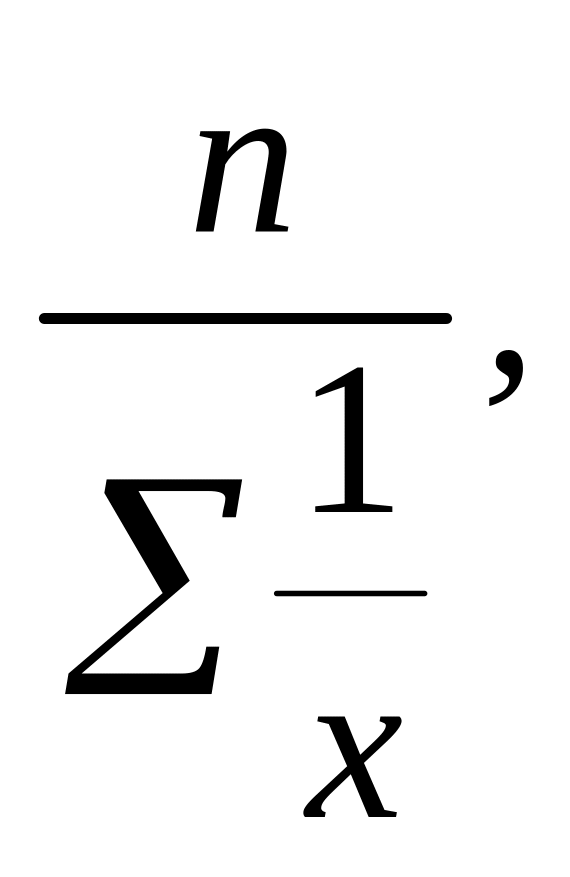
где
– средняя
гармоническая;
1 1 1 1
—; —; —... — – числа, обратные заданным вариантам.
х х1 х2 хп
Иначе говоря, простая гармоническая средняя есть отношение числа вариантов к сумме обратных значений этих вариантов.
Для нашего примера будем иметь:
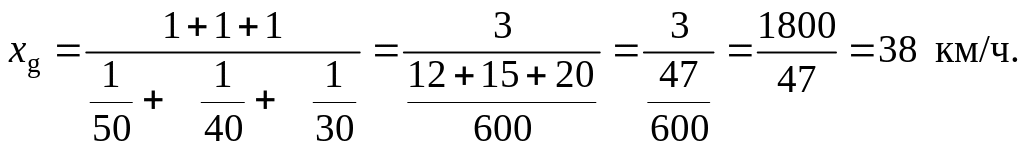
В нашем примере средняя арифметическая (ха) оказалась больше средней гармонической х h.
При
этом абсолютная ошибка завышения
составляет 2 км/ч (38–40), а относительная
– 5 %
.
Таким образом, неправильное использование арифметической средней привело бы к завышению средней скорости движения автомобиля и может привести к неправильному определению объема перевозок.