6.4. Представление отклика линейной цепи в форме интеграла наложения или свертки

Любой детерминированный сигнал можно представить при помощи единичной ступенчатой или единичной импульса функции, называемых в радиоэлектронике единичная ступенька и единичный импульс.

Единичная ступенька (скачок):

(6.26)

Она равна нулю при отрицательных значениях аргумента и единице при положительных. Сдвиг ступеньки по оси времени на интервал видоизменяет выражение (6.26) в

(6.27)

Произвольная ограниченная функция времени , умноженная на , обращается в нуль («отсекается») при и остается без изменений при . Таким образом, умножение на равносильно замыканию ключа, включающего сигнал в момент времени .

Единичный импульс ( -функция, функция Дирака):

(6.28)

При одновременном выполнении условия

(6.29)

При сдвиге импульса по оси времени на интервал выражения (6.28) и (6.29) принимают вид

(6.30)

Единичный импульс представляет собой производную от единичной ступеньки:

, (6.31)

а единичная ступенька – интеграл от единичного импульса:

(6.32)

Если умножить подынтегральное выражение (6.30)на функцию , то не равное нулю значение произведения может иметь место только при , поэтому

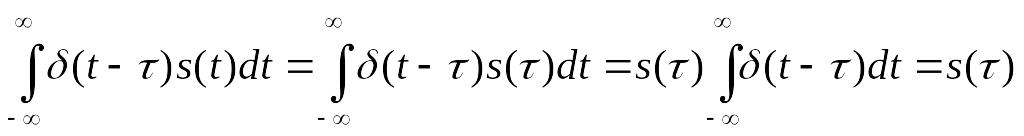(6.33)

Таким образом, единичный импульс производит выборку отдельных значений или стробирует функцию в момент времени .

Отклик (реакция) системы на единичную ступеньку называется переходной характеристикой , отклик системы на единичный импульс – импульсная характеристика - . Импульсная характеристика определяется как производная от переходной: , (6.34)

а переходная – интегралом от импульса:

(6.35)

Пусть к системе с импульсной характеристикой приложен сигнал . С некоторым приближением этот сигнал можно рассматривать как последовательность плотно прилегающих друг к другу коротких импульсов длительностью с амплитудами, равными мгновенным значениям сигнала в момент времени где n- порядковый номер импульса (рис1.4). Заменим короткие импульсы единичными в моменты времени , а их амплитуды приравняем к площадям прямоугольников . При стремлении к нулю точность такого представления функции возрастает.

Рис. 1.4. Сигнал в виде последовательности импульсов

Отклик на n-й импульс пропорционален импульсной характеристике системы, смещенной на время :

(6.36)

В соответствии с принципом суперпозиции отклик на сигнал в целом есть сумма откликов на все элементарные импульсы:

. (6.37)

Или в пределе (6.38)

(6.39)

Выражение (6.38) и (6.39) называют интегралом свертки (интегралом Дюамеля).

Единичные ступеньки и импульс являются идеализацией, на практике мгновенными считают явления, продолжительность которых существенно меньше длительности переходных процессов в исследуемой цепи.