§ 100. Переход от одной декартовой прямоугольной системы координат к другой прямоугольной системы в пространстве

Введем в пространстве две прямоугольные системы координат и с общим началом координат. Обозначим через единичные векторы осей Ох, Оу, Оz, а через - единичные векторы осей (рис. 147).

Координаты единичного вектора в ортонормированном базисе т. е. в базисе, векторы которого единичные и попарно ортогональные, являются косинусами углов между этим единичным вектором и векторами . Обозначая углы между вектором и векторами через углы между и векторами через и углы между вектором и векторами через будем иметь (§ 98)

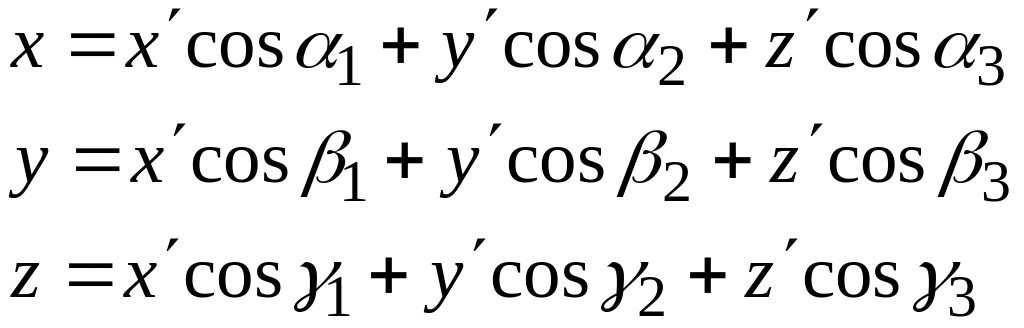(1)

где - координаты произвольной точки М в системе , а - координаты той же точки М в системе .

Матрица перехода имеет вид

.

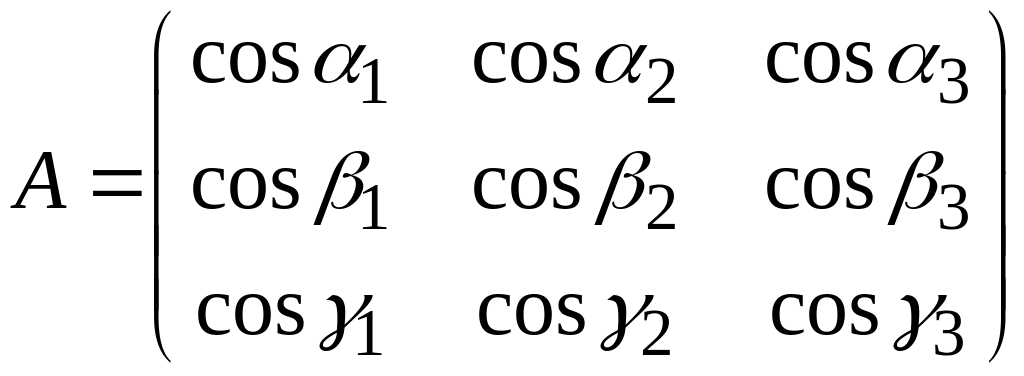
Она ортогональная, т.е. сумма квадратов элементов, расположенных в каждом столбце, равна 1, так как векторы единичные, а сумма произведений соответствующих элементов двух любых различных столбцов равна нулю (т.к. векторы попарно ортогональные).

Так как определитель равен

а векторы - единичные, и попарно ортогональные, то этот определитель равен . Он равен +1, если упорядоченная тройка векторов имеет ту же ориентацию, что и упорядоченная тройка , и – 1, если эти упорядоченные тройки векторов имеют противоположную ориентацию.

Можно сказать и так: детерминант матрицы А равен в зависимости от того, имеют ли системы и одинаковую или противоположную ориентацию.

Отметим частный случай преобразования декартовой прямоугольной системы координат в декартовую прямоугольную той же ориентации при условии, что оси и совпадают. В этом случае формулы (1) принимают вид:

, (2)

где - угол от оси Ох до оси в плоскости хОу, причем ориентацию этой плоскости задаем системой координат хОу. В этом частном случае будем говорить, что система получается из системы поворотом вокруг оси на угол .

Обратно, пусть задана ортогональная матрица порядка:

(3)

т.е.

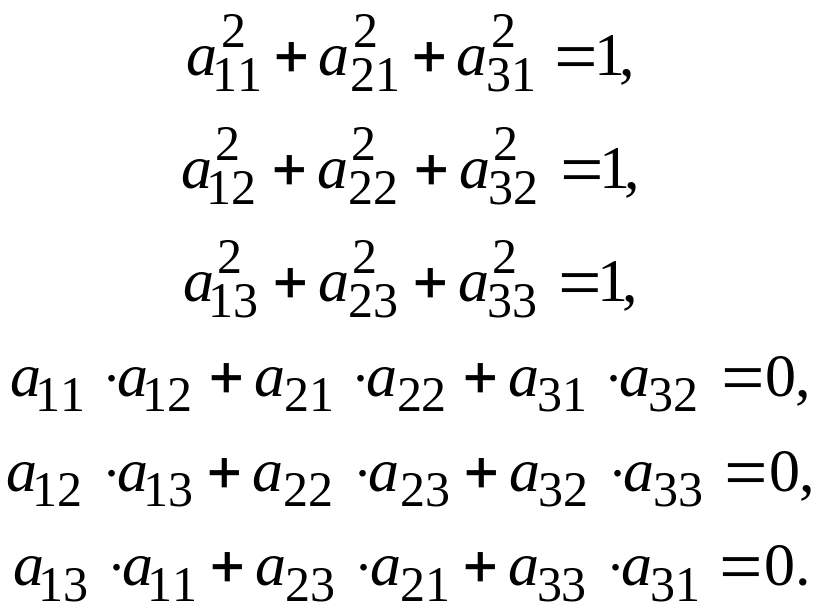(4)

Введем в пространстве прямоугольную систему координат . Векторы

(5)

в силу соотношений (4) единичные и попарно ортогональные. Рассмотрим систему с единичными векторами . Тогда формулы

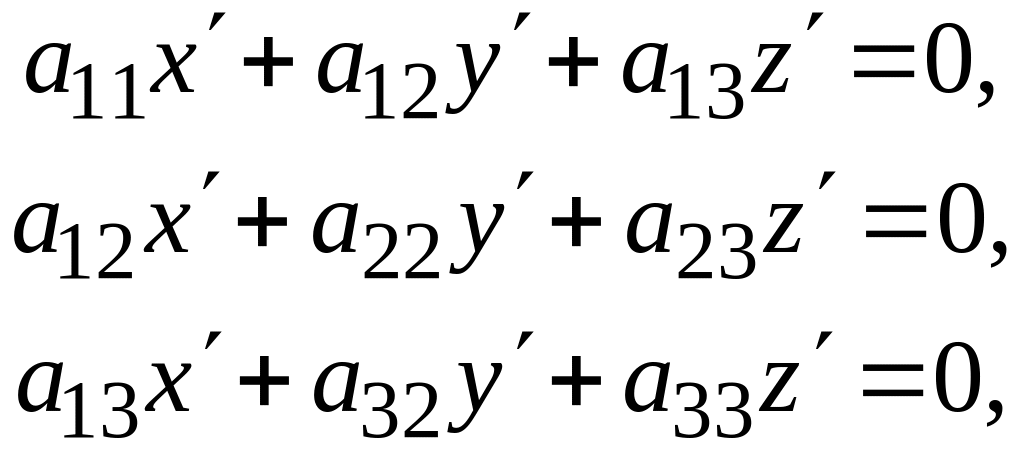
связывают координаты и в одной и той же точке М в системах и .

Если в пространстве введены две декартовы прямоугольные системы координат и , то координаты любой точки М пространства в системе через координаты той же точки в системе выражаются соотношениями (рис. 148).

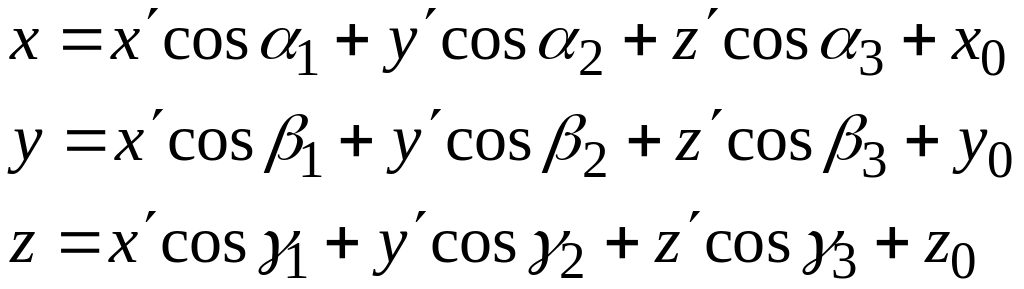
где углы между осями Ох, Оу, Оz, :

	Ох	Оу	Оz

а - координаты точки в системе .

Старые и новые координаты и вектора при общем преобразовании декартовой прямоугольной системы координат в декартову прямоугольную имеют вид