§ 98. Преобразование общей декартовой системы координат в пространстве.

Аналогично доказывается, что если в пространстве введены две общие декартовы системы координат Oxyz и с общим началом О и если масштабные векторы осей Ох, Oy, Оz соответственно а масштабные векторы осей соответственно то, обозначая через х, у, z координаты произвольной точки М пространства в системе Oxyz, а через - координаты той же точки М в системе будем иметь (рис. 143)

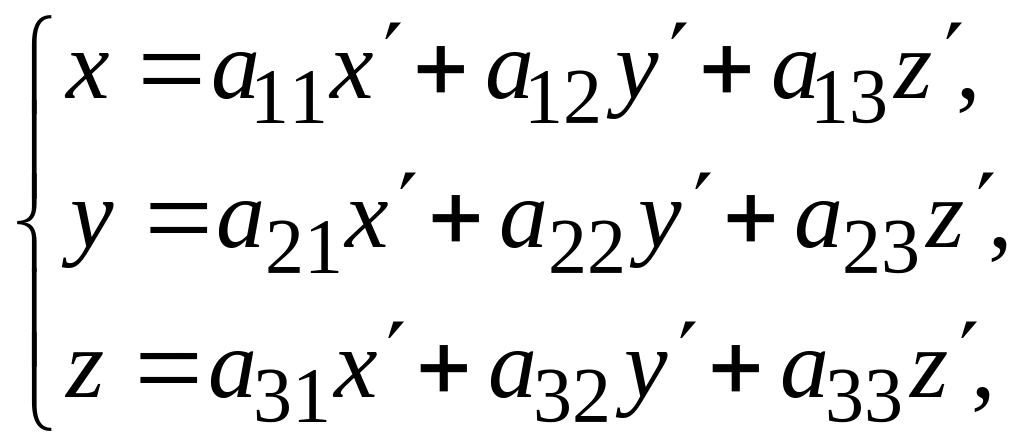(1)

причем (2)

(координаты векторов даны в базисе ) и, далее, матрица перехода

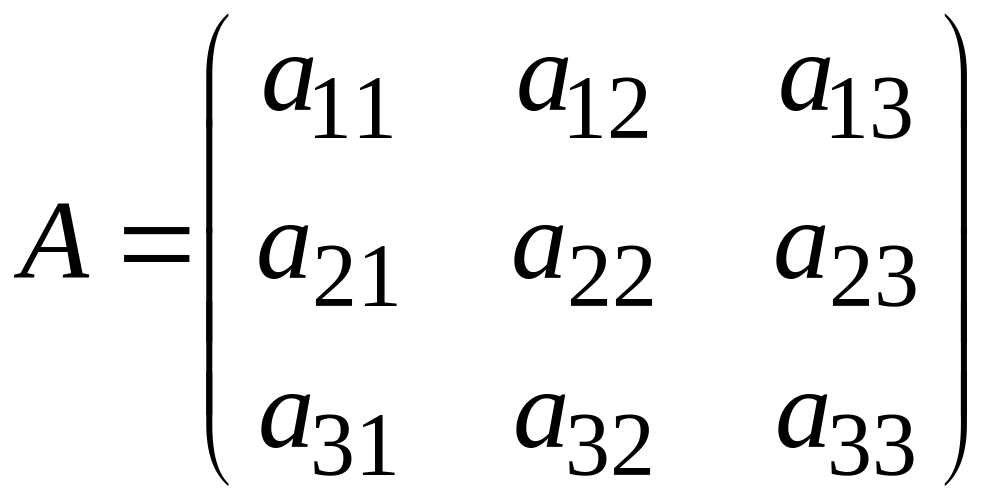(3)

невырожденная т. е.

.

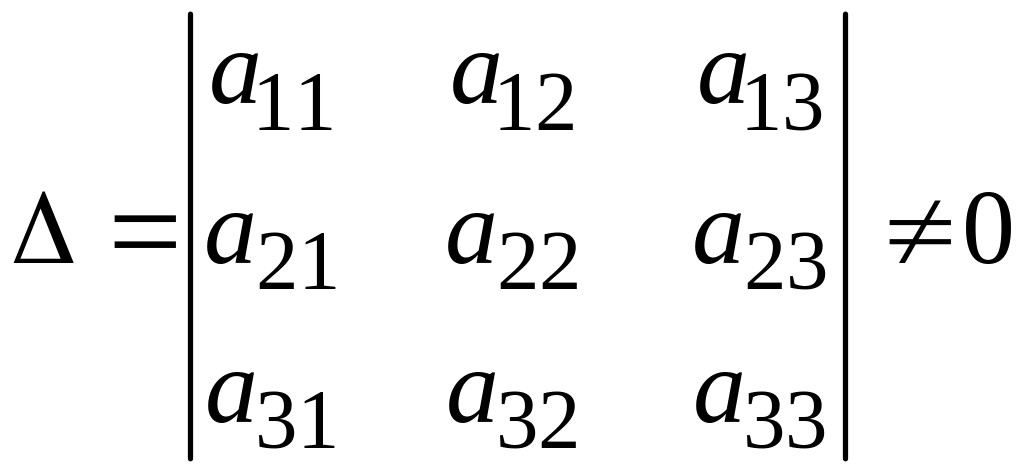Обратно, если А – любая невырожденная матрица и в пространстве введена общая декартова система координат, то соотношения (1) связывают координаты х, у, z и одной и той же точки М пространства в системе с началом координат в точке О и масштабными векторами осей , заданными равенствами (2) относительно системы Oxyz.

Далее. Если в пространстве введены две общие декартовы системы координат Oxyz и (рис. 144), то координаты х, у, z любой точки М пространства в системе Oxyz через координаты той же точки М в системе выражаются соотношениями

(4)

где имеют прежний геометрический смысл, а - координаты начала координат системы в системе Oxyz.

При этом общем преобразовании общей декартовой системы координат х, у, z вектора через его новые координаты выражаются соотношениями:

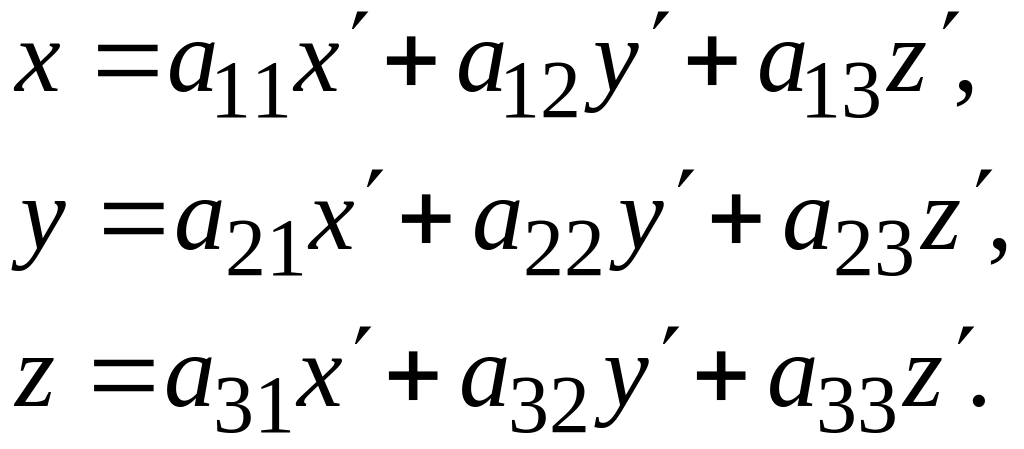
§ 99. Преобразование декартовой прямоугольной системы координат на плоскости.

1) Переход от одной декартовой прямоугольной системы координат на плоскости к другой декартовой прямоугольной системе с той же ориентацией и с тем же началом координат.

Предположим, что на плоскости введены две декартовы прямоугольные системы координат хОу и с общим началом координат О, имеющие одинаковую ориентацию (рис. 145). Обозначим единичные векторы осей Ох и Оу соответственно через и , а единичные векторы осей и через и . Наконец пусть - угол от оси Ох до оси . Пусть х и у – координаты произвольной точки М в системе хОу, а и - координаты той же точки М в системе .

Так как угол от оси Ох до вектора равен , то координаты вектора

Угол от оси Ох до вектора равен 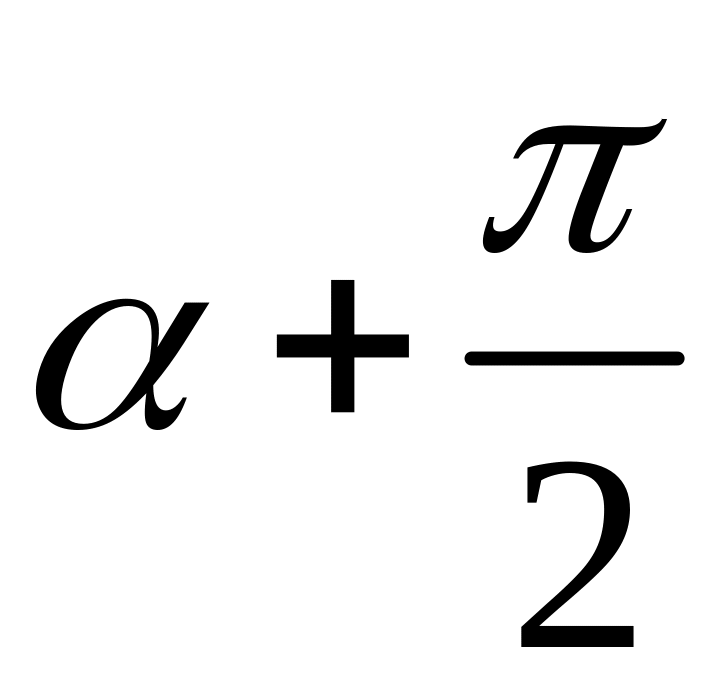; поэтому координаты вектора равны .

.

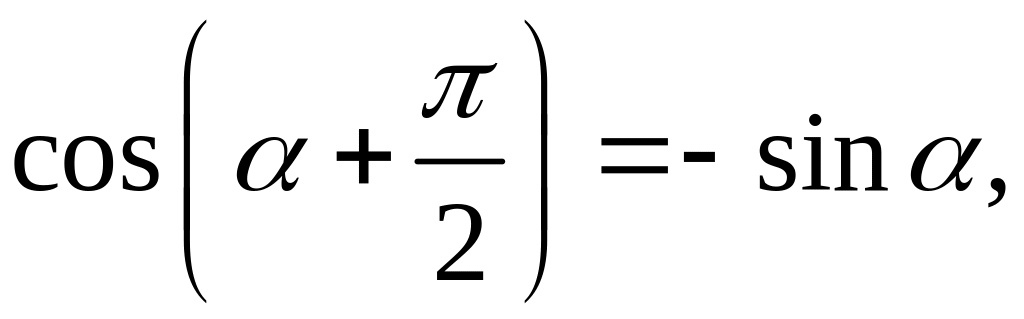Формулы (3) § 97 принимают вид

(1)

Матрица перехода от одной декартовой хОу прямоугольной системы координат к другой прямоугольной системе с той же ориентацией имеет вид

.

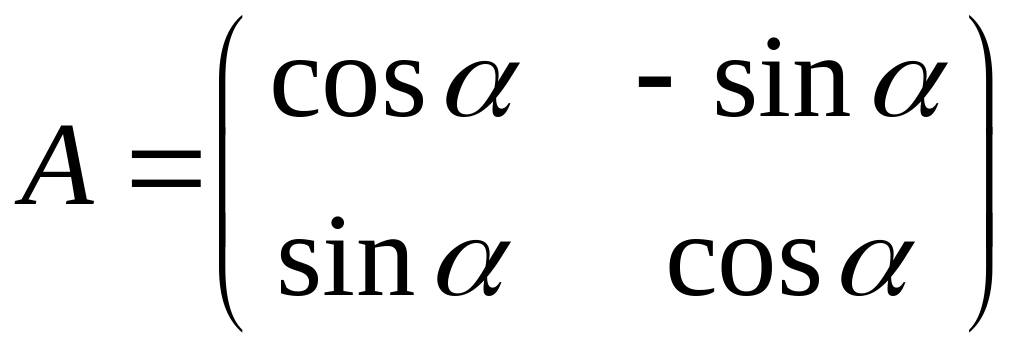Матрица называется ортогональной, если сумма квадратов элементов, расположенных в каждом столбце, равна 1, а сумма произведений соответствующих элементов разных столбцов равна нулю, т.е. если

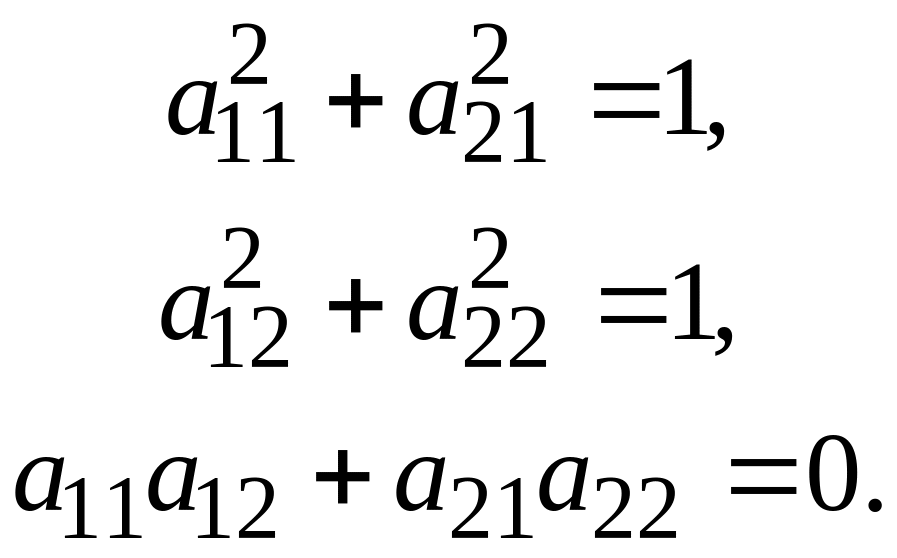(4)

Таким образом, матрица (2) перехода от одной прямоугольной системы координат к другой прямоугольной системе с той же ориентацией ортогональная. Отметим ещё, что определитель этой матрицы равен +1:

.

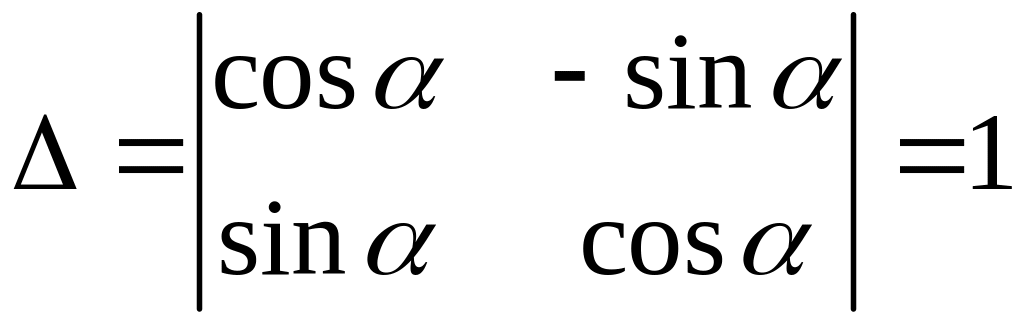Обратно, если задана ортогональная матрица (3) с определителем, равным +1, и на плоскости введена декартова прямоугольная система координат хОу, то в силу соотношений (4) векторы и единичные и взаимно перпендикулярные, следовательно, координаты вектора в системе хОу равны и , где - угол от вектора до вектора , а так как вектор единичный и получим из вектора поворотом на , то либо , либо .

Вторая возможность исключается, так как если бы мы имели , то а нам дано, что .

Значит, , и матрица А имеет вид

,

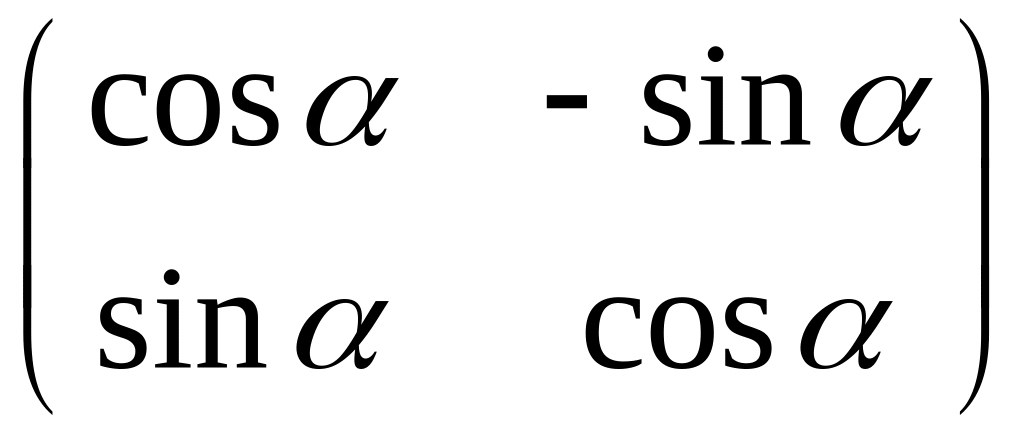т.е. является матрицей перехода от одной прямоугольной системы координат хОу к другой прямоугольной системе , имеющей ту же ориентацию, причем угол .

2. Переход от одной декартовой прямоугольной системы координат на плоскости к другой декартовой прямоугольной системе с противоположной ориентацией и с тем же началом координат.

Пусть на плоскости введены две декартовы прямоугольные системы координат хОу и с общим начало координат О, но имеющие противоположную ориентацию обозначим угол от оси Ох до оси через (ориентацию плоскости зададим системой хОу).

Так как угол от оси Ох до вектора равен , то координаты вектора равны:

.

Теперь угол от вектора до вектора равен 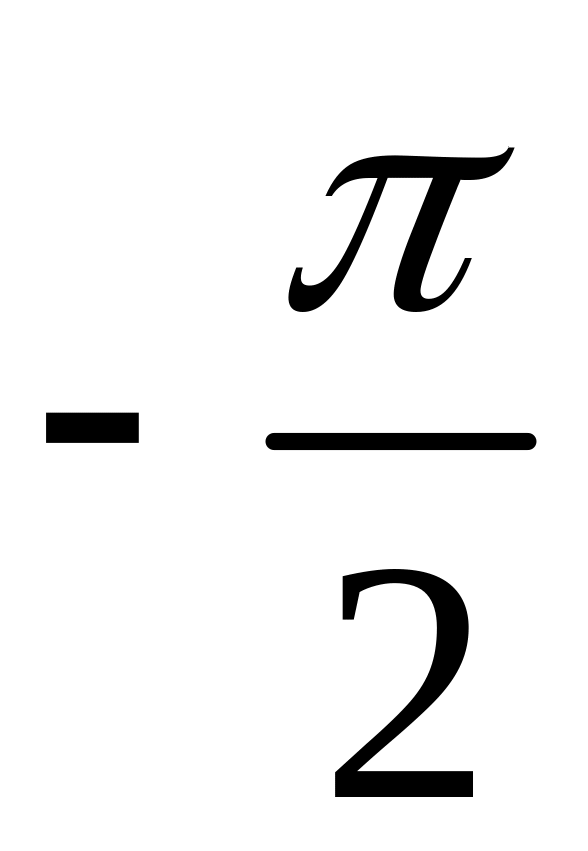(рис. 146), поэтому угол от оси Ох до вектора равен (по теореме Шаля для углов) 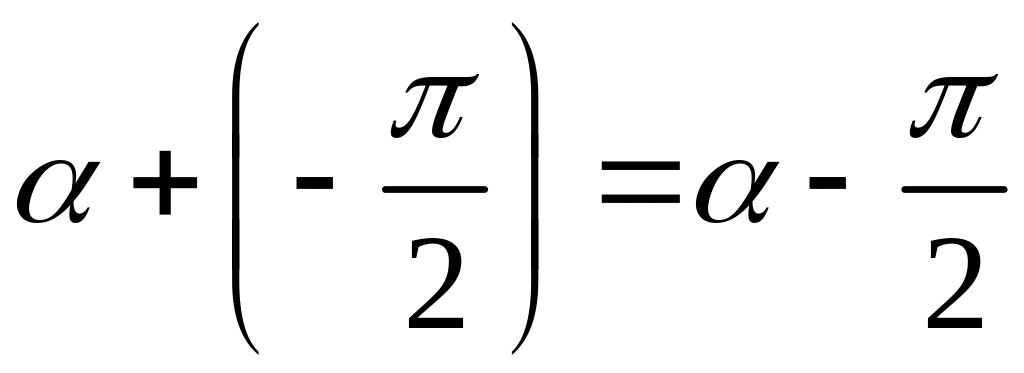и поэтому координаты вектора равны:

.

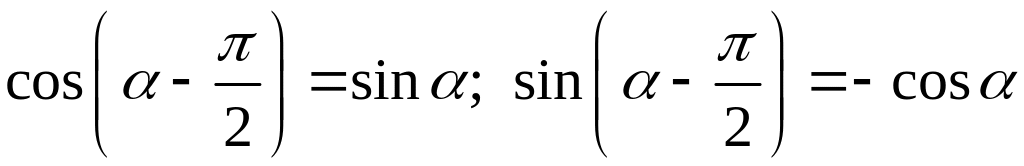И формулы (3) § 97 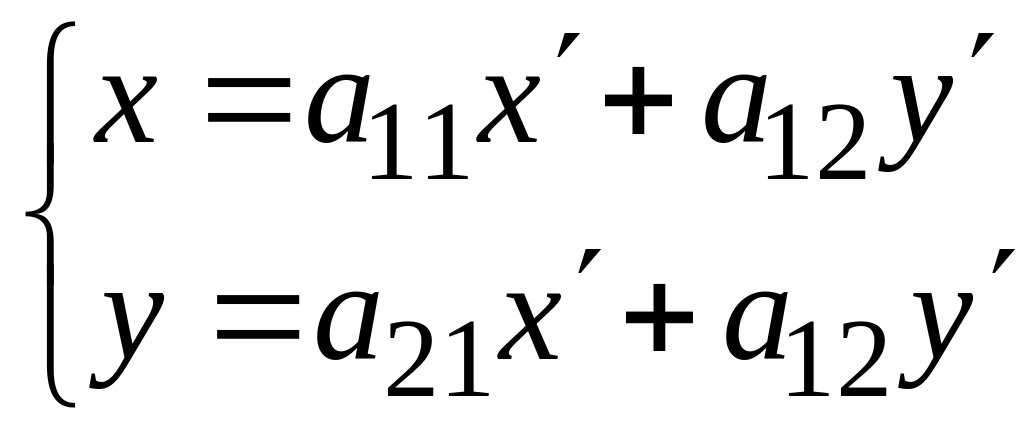принимают вид

(6)

Матрица перехода

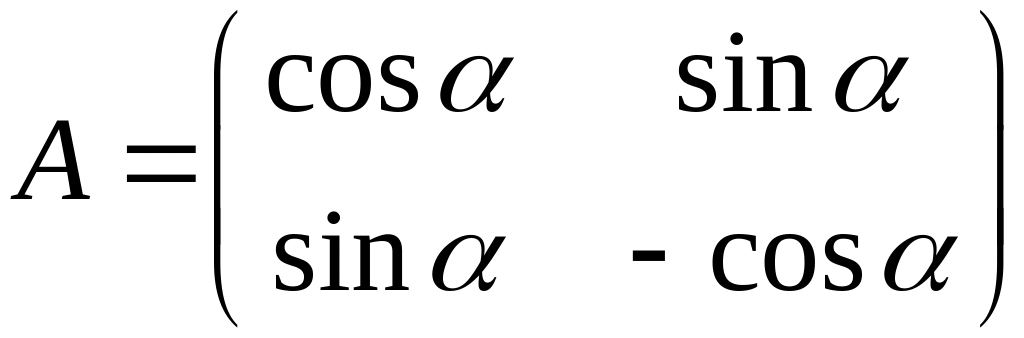
ортогональная, но ее определитель равен –1 . (7)

Обратно, любая ортогональная матрица с определителем, равным –1, задает преобразование одной прямоугольной системы координат на плоскости в другую прямоугольную систему с тем же началом, но противоположной ориентации. Итак, если две декартовы прямоугольные системы координат хОу и имеют общее начало, то

,

где х, у – координаты любой точки в системе хОу; и - координаты той же точки в системе , а

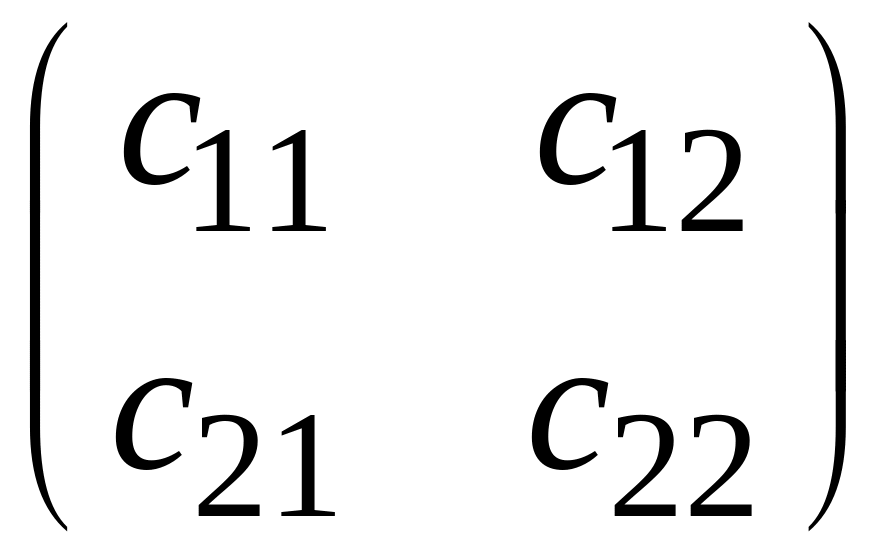
ортогональная матрица.

Обратно, если

произвольная ортогональная матрица, то соотношениями

выражается преобразование декартовой прямоугольной системы координат в декартовую прямоугольную систему с тем же началом координат; - координаты в системе хОу единичного вектора , дающего положительное направление оси ; - координаты в системе хОу единичного вектора , дающего положительное направление оси .

В случае

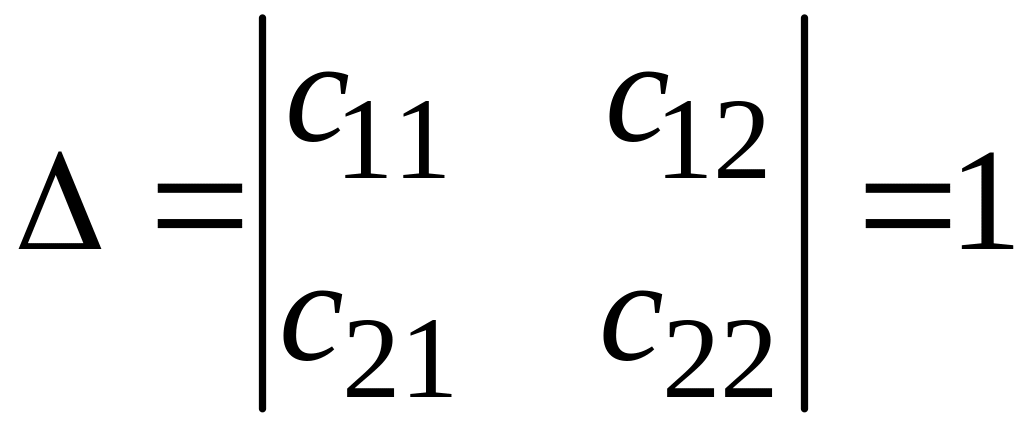
системы координат хОу и имеют одинаковую ориентацию, а в случае - противоположную.

3. Общее преобразование одной декартовой прямоугольной системы координат на плоскости в другую прямоугольную систему.

На основании пунктов 1) и 2) этого параграфа, а также на основании § 96 заключаем, что если на плоскости введены прямоугольные системы координат хОу и , то координаты х и у произвольной точки М плоскости в системе хОу с координатами и той же точки М в системе связаны соотношениями

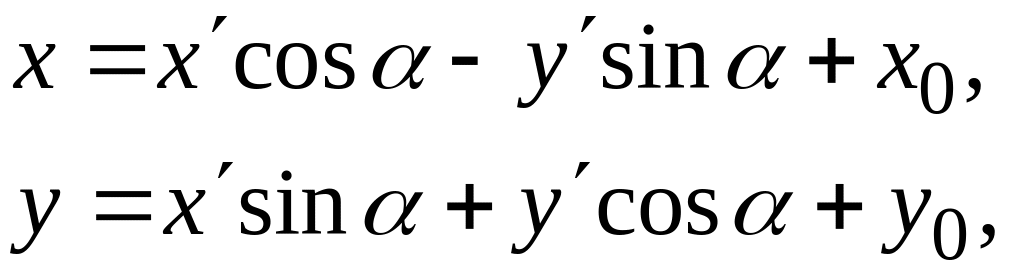(8)

если системы хОу и имеют одинаковую ориентацию, и соотношениями

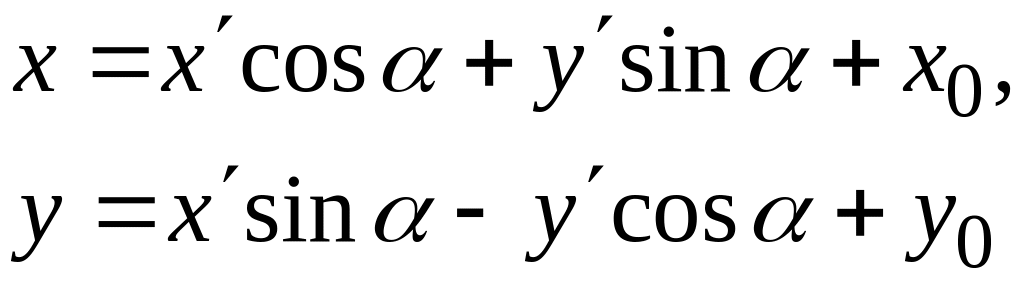(9)

если системы хОу и имеют противоположную ориентацию.

В формулах (8) и (9) и - координаты точки в системе хОу, а , причем ориентация плоскости определяется системой хОу.

Общее преобразование декартовой прямоугольной системы координат в декартову прямоугольную систему можно записать и в виде

, (10)

где

ортогональная матрица, а и - координаты начала системы координат в системе хОу.

Заметим, что старые и новые координаты х, у и , вектора при общем преобразовании декартовой прямоугольной системы координат связаны соотношениями

в случае, если системы хОу и имеют одинаковую ориентацию и соотношениями

в случае, если эти системы имеют противоположную ориентацию, или же в виде

(11)

где

ортогональная матрица. Преобразования (10) и (11) называются ортогональными.