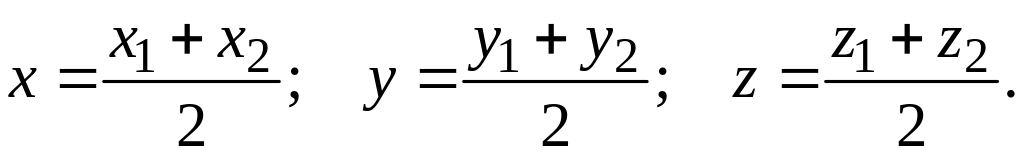§ 13. Деление направленного отрезка в данном отношении.

Теорема 9. Если относительно общей декартовой системы координат на плоскости заданы две различные точки и и точка делит направленный отрезок в отношении , то равна тому из соотношени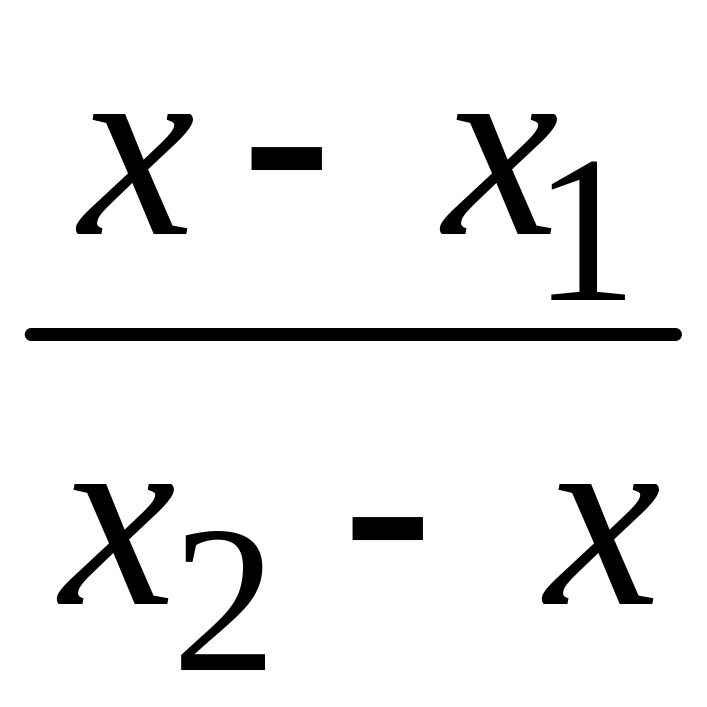й или 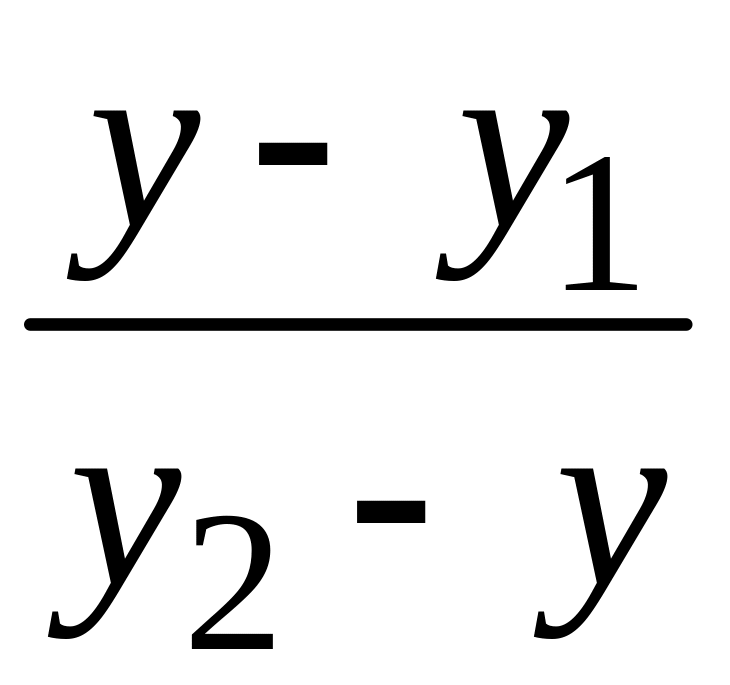, в котором знаменатель не равен нулю, и любому из них 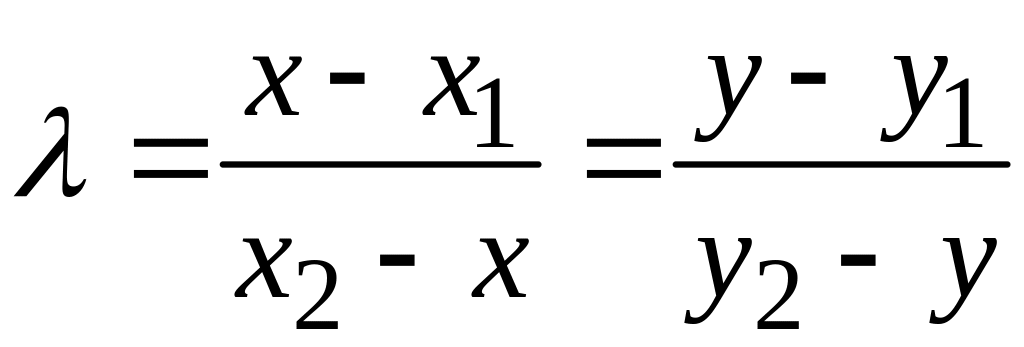, если оба знаменателя . Координаты х, у точки С выражаются через координаты точек А и В соотношениями

Доказательство. Спроектируем точки А, В, С на ось Ох параллельно оси Оу; проекциями будут соответственно точки

Предположим, что точки и различны, т.е. , так как при параллельном проектировании сохраняется порядок точек, лежащих на прямой, и отношение отрезков, лежащих на одной прямой, то точка делит направленный отрезок в том же отношении и, значит (§ 5, теорема 1).

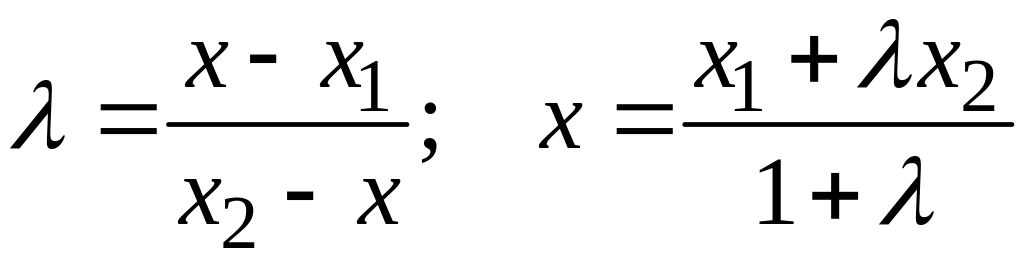
Если точки и совпадают, то с ними совпадает и точка , т.е. . формула в этом случае не имеет места, однако формула верна, так как при правая часть обращается в . Аналогично доказывается и остальная часть теоремы.

Следствие. Координаты середины отрезка равны полусуммам его концов.

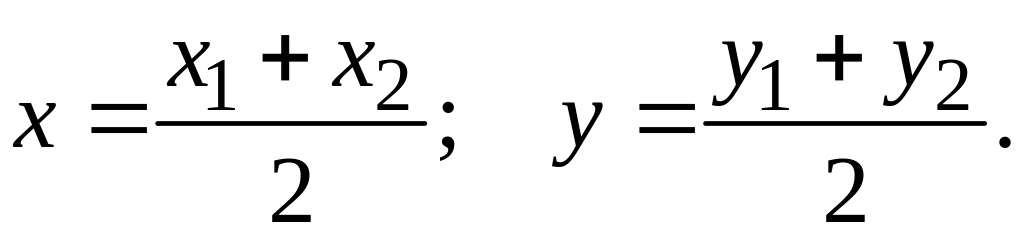
Теорема 10. Если относительно общей декартовой системы координат в пространстве заданы 2 различные точки и и точка делит направленный отрезок в отношении , то равно тому из отношений

.

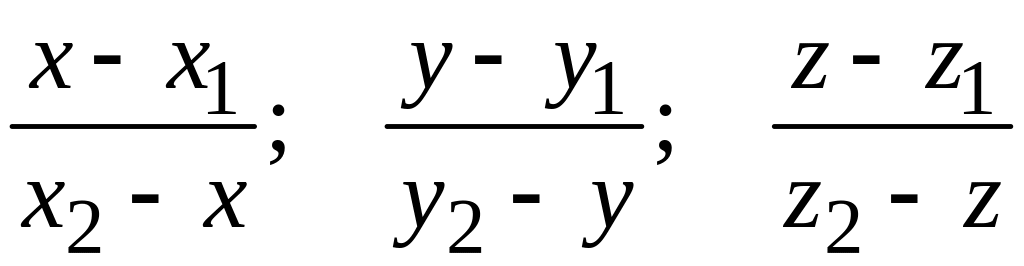В котором знаменатель не равен нулю, и любому из них: 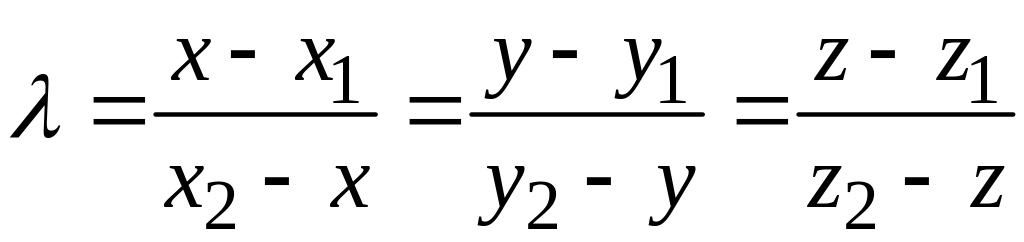если все знаменатели не равны нулю. Координаты точки С через координаты точек А и В выражаются соотношениями

.

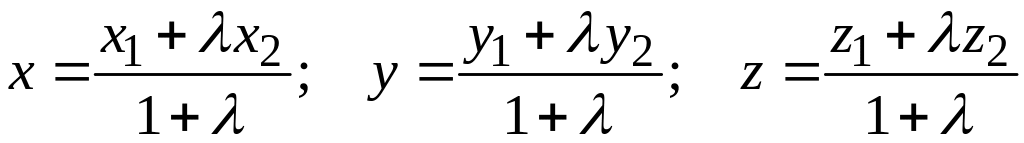Доказательство аналогично предыдущему, здесь только надо проектировать на оси координат параллельно координатным плоскостям.

Следствие. Координаты середины отрезка равны полусуммам координат его концов.