§ 12. Расстояние между двумя точками на плоскости и в пространстве.

Теорема 7. Расстояние d между двумя точками и , заданными относительно прямоугольной системы координат на плоскости, равно корню квадратному из суммы квадратов разностей соответствующих координат этих точек, т.е.

Доказательство. Предположим сначала, что и . Рассмотрим точку . Пусть и - проекции точек и на ось Ох, а и - проекции точек и на ось Оу.

На основании теоремы 3 из § 4 длины отрезков и равны

.

Так как точки и имеют одинаковые ординаты, то отрезок лежит на прямой, параллельно оси Ох, или на самой оси Ох. Поэтому длина отрезка равна длине отрезка :

.

Аналогично доказывается, что

.

Далее, - прямоугольный , так как отрезок лежит на прямой, параллельной оси Ох, или на самой оси Ох, а отрезок лежит на прямой, параллельной оси Оу, или на самой оси Оу. Значит

,

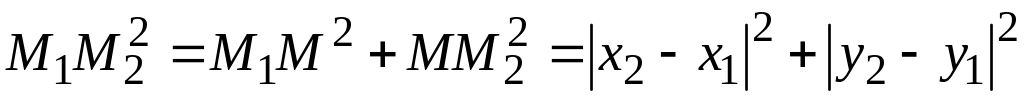или, обозначая через d и замечая, что квадрат модуля этого числа равен квадрату самого этого числа, получим

, откуда следует

ЧТД.

Если , или то под корнем одно из слагаемых обнуляется, но формула остается верной.

Теперь предположим, что направленный отрезок - ненулевой. Из предыдущих рассуждений ясно, что координаты проекций этого направленного отрезка на оси Ох и Оу соответственно равны и . С другой стороны обозначая через и углы направленного отрезка с осями Ох и Оу видно, что координаты проекций равны:

и , где d – длина отрезка .

Итак , ,

Откуда . .

Косинусы углов и , которые образует направленный отрезок с осями Ох и Оу, называются его направляющими косинусами.

Видно, что

Следствие. Расстояние r от точки до начала координат (в декартовой прямоугольной системе координат) и направляющие конусы направленного отрезка :

.

Теорема 8. Расстояние d между двумя точками и заданными относительно декартовой прямоугольной системы координат в пространстве, равно квадратному корню из суммы квадратов разностей соответствующих координат этих точек, т.е.

.

Доказательство. Предположим сначала, что Рассмотрим точку . Пусть и - проекции точек и на плоскость хОу. А и - проекции точек и - на ось Оz. На основании теоремы 1 этого параграфа и теоремы 3 § 4 имеем.

Так как точки и М имеют одинаковую аппликату, то отрезок лежит в плоскости, параллельной плоскости хОу, или в самой этой плоскости, а это значит . Далее, так как точки М и имеют соответственно одинаковые абсциссы и ординаты (они лежат на одной вертикали) поэтому отрезок лежит или на прямой, параллельной оси Оz, или на самой оси Оz; следовательно, Из предыдущих рассуждений следует также, что прямоугольный , поэтому

.

Но ; а .

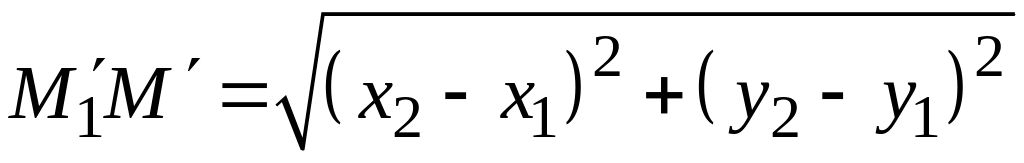Отсюда следует, что

или: , где d – длина отрезка . Значит

Если какие-то координаты равны то формула сохраняется или .

Рассуждениями, аналогичными тем которые мы проводим для плоскости, получим формулы:

,

где - углы ненулевого направленного отрезка соответственно с осями Ох, Оу, Оz: d – его длина; - координата начала ; - координаты конца . Для трехмерного случая справедлива формула Аналогично расстояние r от начала координат до точки находится: