§ 11. Координаты вектора на плоскости и в пространстве

Определение. Проекцией вектора называется вектор , где и – проекции точек А и В. (Под проекцией понимается любой из 3 видов параллельного проектирования: на линию, на плоскость и т.д.)

Это определение обосновывается следующей теоремой.

Теорема 1. Проекции равных направленных отрезков равны.

Доказательство. Пусть . Обозначим проекцию направленного отрезка через , а проекцию направленного отрезка через . Так как , то середина отрезка AD совпадает с серединой отрезка ВС (теорема §7. Условие необходимости), а так как при параллельном проектировании середина отрезка проектируется в середину его проекции, то середина отрезка совпадает с серединой отрезка , а значит (теорема §7. Условие достаточности): . ЧТД.

Введем на плоскости общую декартовую систему координат. Пусть произвольный вектор, лежащий в этой плоскости, и - его проекции на оси Ох и Оу параллельно осям Оу и Ох (См.рис. 18).

Координатами вектора в общей декартовой системе координат называются числа х, у где х - координата вектора на оси Ох, а у – координата вектора на оси Оу.

А налогично определяются координаты вектора в общей декартовой системе координат в пространстве: это упорядоченная тройка чисел х, у, z, где х – координата на оси Ох проекции вектора на ось Ох параллельно плоскости уОz и т.д. (рис.19)

Если вектор имеет координаты х и у (на плоскости) или х, у, z (в пространстве), то будем обозначать это на плоскости и (в пространстве) и писать ; и соответственно .

Из теоремы 1 и определения координат точки следует, что координаты вектора являются координатами его конца Р, если вектор отложен от начала координат:

.

Итак, вводя на плоскости общую декартову систему координат, можно каждому вектору этой плоскости поставить в соответствие упорядоченную пару чисел х, у - координат этого вектора в выбранной системе координат. Обратно, каждая упорядоченная пара чисел х, у является координатами некоторого вектора . Для построения этого вектора достаточно построить точку Р(х,у) в выбранной системе координат. Класс всех направленных отрезков, равных направленному отрезку , и является вектором с координатами х и у.

Аналогичное положение имеет место и в пространстве.

Это соответствие между векторами плоскости и упорядоченными парами чисел (и соответственно между векторами пространства и упорядоченными тройками чисел) взаимно однозначно, так как два вектора и равны тогда и только тогда, когда равны их соответствующие координаты.

В самом деле, отложим векторы и от начала координат:

Соотношение имеет место тогда и только тогда, когда точки Р и Q совпадают, т.е. тогда и только тогда, когда равны их соответствующие координаты.

Теорема 2. Если вектор задан своим началом и концом относительно общей декартовой системы координат, то его координаты х и у вычисляются по формулам .

Доказательство. Пусть и - проекции точек А и В на ось Ох параллельно оси Оу. Тогда вектор является проекцией вектора на ось Ох параллельно оси Оу; теперь на основании определения координаты вектора и теоремы 2 §4 имеем:

.

Аналогично выводиться формула .

Теорема 3. Если вектор задан своим началом и концом относительно общей декартовой системы координат в пространстве, то его координаты x, y, z вычисляются по формулам.

.

Доказательство аналогично.

Теорема 4. Координата ортогональной проекции вектора на ось равна длине АВ этого вектора, умноженной на косинус угла между вектором и осью :

коорд. пр.

Доказательство. Так как проекции равных направленных отрезков равны между собой, то можно считать, что вектор отложен от произвольной точки А оси . Обозначим тогда через С ортогональную проекцию точки В на ось . Если вектор ненулевой и угол между вектором и осью острый (рис.20), то

коорд. пр.

с. 190000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Если вектор ненулевой и угол между вектором и осью тупой (рис.21), то

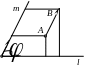Теорема 5. Пусть l и m – две оси, образующие между собой угол . Пусть - вектор, коллинеарный оси m, а - его координата на этой оси. Тогда координата ортогональной проекции вектора на ось l равна координате этого вектора на оси m, умноженной на косинус угла между осями l и m.

Доказательство. Если направление вектора совпадает с направлением оси m, то , а кроме того, угол между осями l и m равен углу между вектором и осью l. Поэтому на основании предыдущей теоремы

коорд. пр.

Если же направление вектора противоположно направлению оси m, то , а, кроме того, угол между вектором и осью l равен . Поэтому на основании предыдущей теоремы

Определение. Назовем ломаной упорядоченную совокупность n точек пространства (порядок точек определяется порядком их записи). Направленные отрезки будем называть звеньям ломаной, а - замыкающей ломаной .

Теорема 6. Координата проекции замыкающей ломаной на ось равна сумме координат проекций ее звеньев на ту же ось.

Доказательство. Пусть - соответственно проекции точек на ось l. Тогда на основании теоремы Шаля имеем: