Лекция №2.

§ 8. Параллельное проектирование

В геометрии рассматриваются следующие три вида параллельного проектирования.

1. Проекция точки М на прямую l параллельно прямой m. Пусть на плоскости заданы две пересекающиеся в точке О прямые l и m.

Е

l

сли точка М не лежит на прямой m, то проекцией точки М на прямую l параллельно прямой m называется точка пересечения прямой l с прямой, проходящей через точку М параллельно прямой m. Если же точка М лежит на прямой m, то ее проекцией на прямую l параллельно прямой m называют точку О. (См. рис. 7).

Если прямые l и m взаимно перпендикулярны, то такое проектирование будет ортогональным.

2. Проекция точки М на плоскость параллельно прямой l.

Пусть в пространстве задана плоскость и пересекающая ее в точке О прямая l. Если точка М не лежит на прямой l, то проекцией ее на плоскость параллельно прямой l называется точка пересечения плоскости с прямой, переходящей через точку М параллельно прямой l. Если точка М лежит на прямой l, то ее проекцией будет точка О.

Е сли прямая l перпендикулярна плоскости , то такое проектирование называется ортогональным. (См. рис. 8)

3) Проекция точки М на прямую l параллельно плоскости .

Пусть в пространстве задана плоскость и пересекающая ее в точке О прямая l. Е сли точка М не лежит на плоскости , то ее проекцией на прямую l параллельно плоскости называется точка пересечения прямой l с плоскостью, проходящей через точку М параллельно плоскости . Если же точка М лежит на плоскости то ее проекцией будет точка О.

Если прямая l перпендикулярна плоскости , то такое проектирование ортогонально. (См. рис. 9)

§ 9.Общая декартова и декартова прямоугольная система координат на плоскости.

Общей декартовой (или афинной) системой координат на плоскости называется упорядоченная совокупность двух пересекающихся осей координат с общим началом координат О на каждой из них (рис.10).

Масштабные отрезки этих осей могут быть различны. Первая ось называется осью Ох, или осью абсцисс, вторая - осью Оу, или осью ординат.

П усть М – произвольная точка плоскости. (См. рис.10). Пусть Р – проекция точки М на ось Ох параллельно оси Оу, а х – координата точки Р на оси Ох; Q – проекция точки М на ось Оу параллельно оси Ох, а у – координата точки Q на оси Оу. Числа х и у называют- Рис. 10

ся общими декартовыми (или аффинными) координатами точки М. Первая координата х называется абсциссой точки М, вторая координата у называется ординатой точки М. Точка М с координатами х, у обозначается так М(х,у). Абсцисса точки М равна нулю тогда и только тогда, когда точка М лежит на оси Оу. Аналогично ордината точки.

В начале координат х=0 и у=0. Точки и называются единичными точками осей координат. Точка называется единичной точкой системы координат, параллелограмм - масштабным параллелограммом.

Отрезки и являются масштабными отрезками соответственно осей Ох и Оу. Векторы ; называются масштабными векторами соответственно осей Ох и Оу.

При помощи общей декартовой системы координат на плоскости устанавливается взаимно однозначное соответствие между множеством всех точек плоскости и множеством всех упорядоченных пар действительных чисел, так как:

1. каждой точке М плоскости соответствует одна определенная упорядоченная пара действительных чисел х, у - координат этой точки;

2. каждая упорядоченная пара х, у действительных чисел становится в соответствие одной и только одной точке М, для которой первое число х – абсцисса, а второе число у – ордината.

Для построения этой точки М в случае , надо построить на оси Ох точку Р с координатой х, а на оси Оу – точку Q с координатой у. Точка М является точкой пересечения прямых, проходящих через точки Р и Q, параллельных соответственно осям Оу и Ох.

Е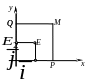 сли у=0 или х=0, то дело сводится к построению точки на оси Ох или на оси Оу.

Декартовой прямоугольной системой координат на плоскости называется упорядоченная совокупность двух взаимно перпендикулярных осей координат с равными масштабными отрезками: и и с общим началом координат О на каждой оси.

Декартовы прямоугольные координаты точки определяются аналогично.

Отметим, что масштабные векторы осей Ох и Оу в декартовой прямоугольной системе координат обозначаются так:

.