5. Графики в полярных координатах

5.1. Полярные координаты

Положение точки в полярных координатах на плоскости (см. рис. 28) определяется:

1) ее расстоянием от некоторой данной точки , называемой полюсом;

2) углом , который образует отрезок с заданным направлением прямой , которая называется полярной осью).

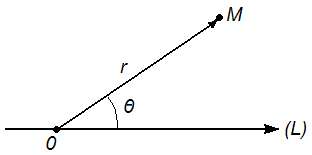
Рис. 28. Точка в полярных координатах.

При этом называют радиусом-вектором и - полярным углом. Если принять полярную ось за , а полюс - за начало координат, то имеем, очевидно (см. рис. 29):

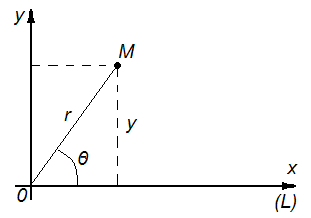
Рис. 29. Точка в полярных координатах.

Данному положению точки соответствует одно определенное положительное значение и бесчисленное множество значений , которые отличаются слагаемым, кратным . Если совпадает с , то и - неопределенно.

Всякая функциональная зависимость вида (явная) или (неявная) имеет в полярной системе координат свой график.

В дальнейшем мы будем рассматривать не только положительные, но и отрицательные значения , причем если некоторому значению соответствует отрицательное значение , то условимся откладывать это значение в направлении, прямо противоположном тому направлению, которое определяется значением .

5.2. Графики кривых в полярных координатах

Для того, чтобы построить график в полярных координатах по точкам нужно заполнить таблицу, в первой строке которой записать значения угла из интересующего промежутка, а во второй - соответствующие значения функции . Затем, отметить и соединить эти точки плавной линией.

Построим графики функций, которые часто бывают заданы в полярных координатах.

Спирали. Пусть , . Рассмотрим три вида спиралей:

• спираль Архимеда: ,

• гиперболическая спираль:

• логарифмическая спираль: .

Спираль Архимеда . График функции имеет вид, изображенный на рис. 30 а), причем пунктир соответствует части кривой при . Отрицательным значениям соответствуют и отрицательные значения , и их надо откладывать в направлении, противоположном тому направлению, которое определяется значением . При этом заполнять таблицу значений и нет необходимости в силу простой функциональной завиимости между и .

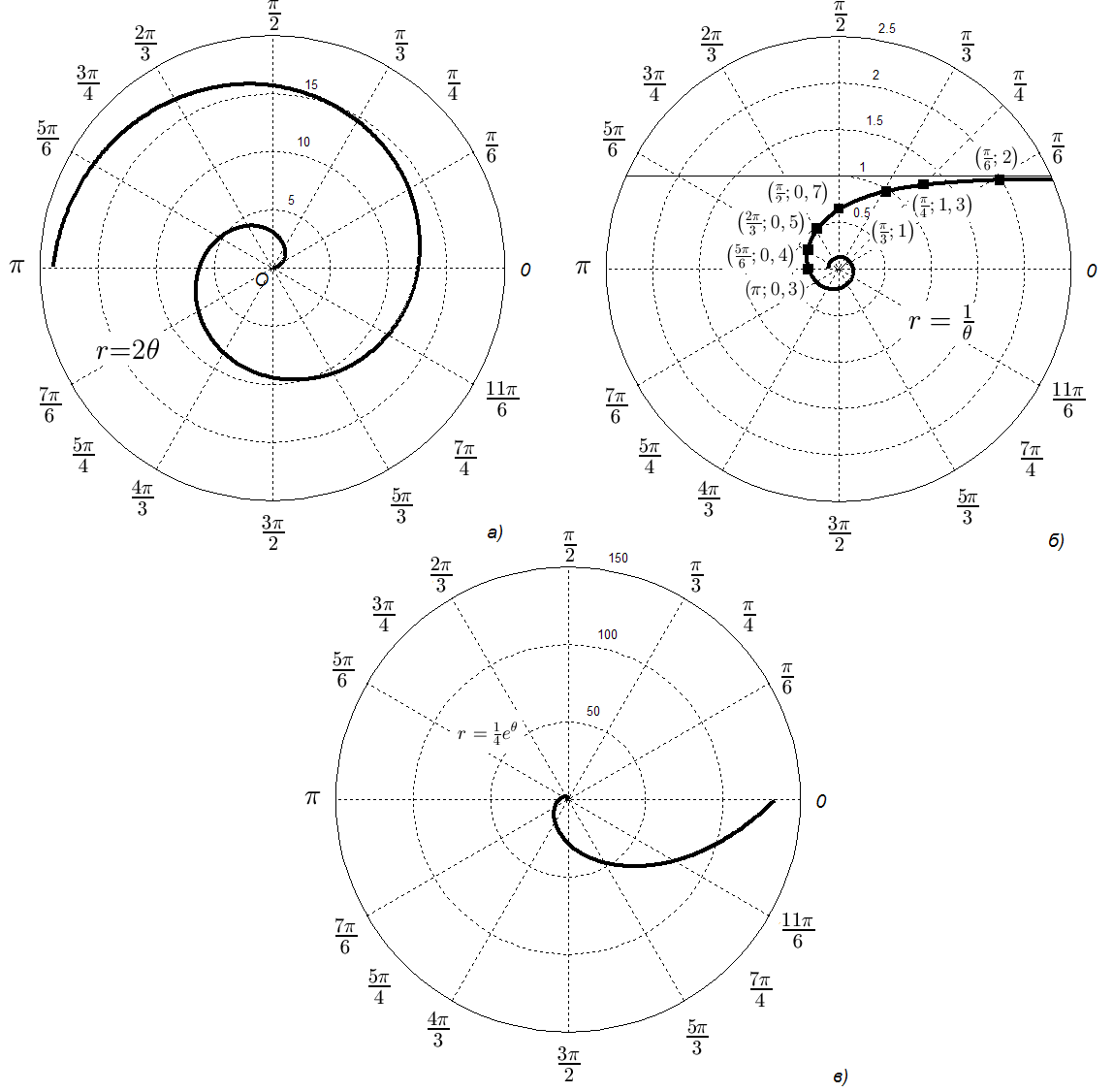
Рис. 30. Графики функций , и .

Гиперболическая спираль . Особенностью этого графика (см. рис. 30 б) является то, что расстояние между любой точкой этой кривой и полярной осью не превосходит (т.е. кривая имеет асимптоту, параллельную полярной оси и проведенную на расстоянии от нее).

Предполагая и заполним таблицу для и .

Таблица 4.

Замечаем, что будет увеличиваться при уменьшении . При этом, график не имеет общих точек с прямой, параллельной полярной оси и проходящей на расстоянии от неё. Далее, видим, что не обращается в нуль ни при каких конечных значениях , а только будет уменьшаться с увеличением . Кривая будет поэтому беспредельно приближаться к полюсу , закручиваясь около него, но никогда не пройдет через в противоположность спирали Архимеда.

Отметив и соединив плавной линией точки таблицы 2, а также учитывая поведение функции при увеличении и уменьшении угла получим график функции (см. рис. 30 б).

Логарифмическая спираль . При имеем . Если , то при увеличении увеличивается и . Если , то при уменьшении радиус-вектор приближается к нулю.

Логарифмическая спираль изображена на рис. 30 в.

Розы. Розами, или кривыми Гвидо Гранди, называютя кривые, полярное уравнение которых имеет вид или . Будем рассматривать случай, когда , - целое положительное число.

Заметим, что поскольку правая часть уравнения розы не может превышать , то вся кривая находится внутри круга радиуса . Так как и являются переодическими функциями, то роза состоит из лепетков, симметричных относительно наибольших радиусов, каждый из которых равен . При этом если нечетное число, то число лепестков равно , а если - чётное, то роза имеет лепестков.

Графики функций , , и изображены на рис. 31.

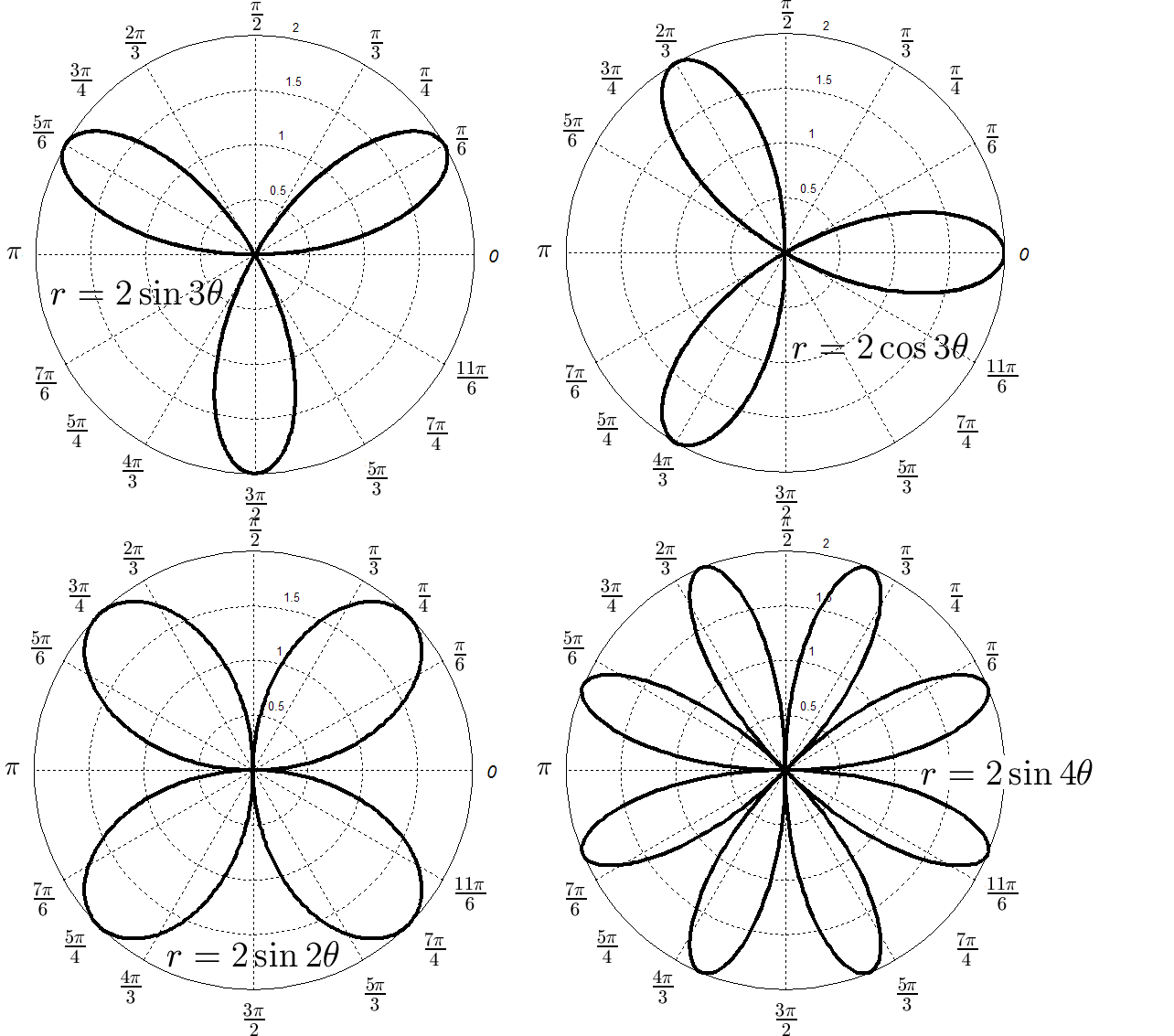
Рис. 31. Графики функций , , и .

Улитка Паскаля и кардиоида. Полярное уравнение улитки имеет вид . Если , то это уравнение дает только положительные значения (см. рис. 32 a)). Если , то будет принимать и отрицательные значения (см. рис. 32 б)). Наконец, при уравнение улитки будет и в этом случае улитка представляет собою кардиоиду (см. рис. 32 в)).

В качестве примера приведем графики функций , и на рис. 32.

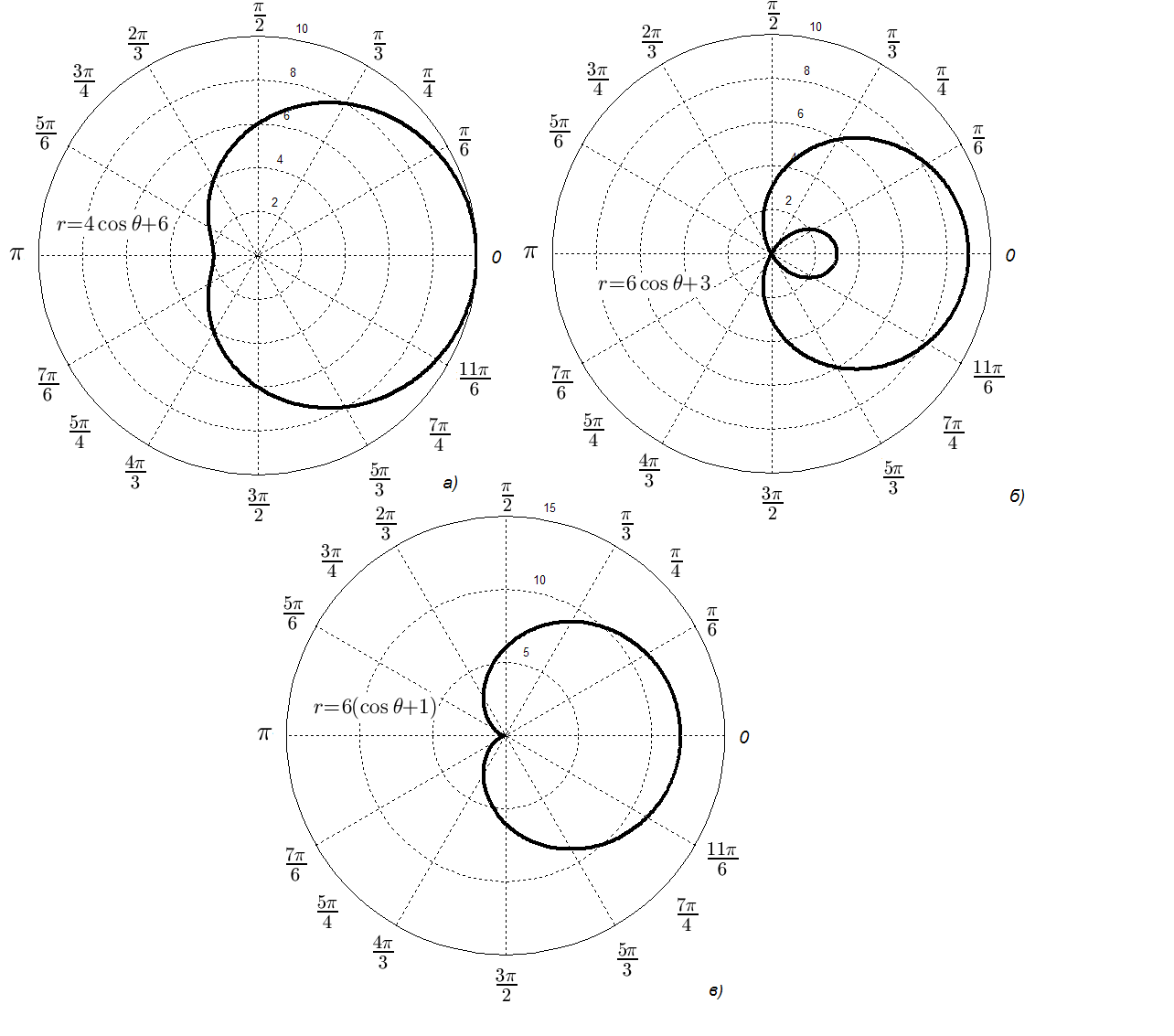
Рис. 32. Графики функций , и .