
- •Ряды Контрольная работа № 8
- •Санкт-петербург
- •§1. Основные понятия
- •Определения.
- •Необходимый признак сходимости.
- •§2. Признаки сходимости
- •Исследование на сходимость рядов с положительными членами.
- •Признак сравнения.
- •§3. Функциональные ряды
- •3.1. Область сходимости.
- •3.2. Правильная сходимость функциональных рядов.
- •§4. Степенные ряды
- •4.1. Интервал и радиус сходимости.
- •4.2. Ряд Тейлора.
- •4.3. Применение таблицы простейших разложений.
- •§5. Приложения степенных рядов к приближенным вычислениям
- •5.1. Приближенное вычисление логарифмов.
- •5.2. Приближенное вычисление корней.
- •5.3. Приближенное вычисление определенных интегралов.
- •II. Пример выполнения контрольной работы.
- •Задание 591-600.
- •Задание 601-610.
- •Задание 611-620.
- •Задание 621-630.
Задание 611-620.
Пример 9.
Найти область
сходимости ряда
![]() .
.
Решение.
Применим признак Коши
![]() .
.![]()
Отсюда видно, что ряд сходится при положительных x и расходится при отрицательных. В точке x=0 этот ряд обращается в числовой ряд
1+1+1+1+…+1+… , который очевидно расходится.
Таким образом, для данного ряда область сходимости представляет собой интервал 0 < x <+ ∞.
Пример 10.
Определить радиус, интервал сходимости и выяснить поведение на концах интервала сходимости степенного ряда
![]()
Решение.
![]()
поэтому (по признаку Даламбера) данный степенной ряд будет сходиться абсолютно для тех значений, для которых
![]() ,
,
таким образом
![]() .
.
Следовательно,
радиус сходимости R
=
![]() ,
а интервал сходимости (–
,
).
,
а интервал сходимости (–
,
).
Теперь исследуем поведение ряда на концах интервала сходимости. В левом конце, при x = – , данный степенной ряд превращается в числовой ряд
![]() ,
,
который сходится
по теореме Лейбница (ряд знакочередующийся,
члены ряда монотонно убывают и
![]() ).
).
В правом конце,
при x
=
![]() ,
получается числовой ряд
,
получается числовой ряд
![]() .
.
Так как последний
ряд – знакоположительный ряд, используем
предельную форму признака сравнения и
сравним со сходящимся рядом
![]() :
:
 ,
,
Таким образом, ряд в правом конце интервала – тоже сходящийся.
Следовательно,
интервал сходимости для данного ряда
![]() .
.
Задание 621-630.
Пример 11.
Разложить в ряд
по степеням x
функцию
![]() .
.
Решение.
Найдем производные функции f(x) и их значения в точке x=0:

Проверим, будет ли выполняться: при .
Для этого оценим абсолютную величину остаточного члена :
 .
.
Для ряда
![]()
при всех x,
следовательно, по признаку Даламбера
ряд
сходится,
а его общий член
![]() при
(по
необходимому признаку сходимости).
Поэтому и остаточный член
,
имеющий модуль, меньший
при
(по
необходимому признаку сходимости).
Поэтому и остаточный член
,
имеющий модуль, меньший
![]() ,
тем более стремится к нулю при всех x.
Таким образом, данная функция раскладывается
в ряд Маклорена (т.к. слова «по степеням
x»
означают, что в формуле ряда Тейлора
a=0):
,
тем более стремится к нулю при всех x.
Таким образом, данная функция раскладывается
в ряд Маклорена (т.к. слова «по степеням
x»
означают, что в формуле ряда Тейлора
a=0):
 (- ∞ < x
< + ∞).
(- ∞ < x
< + ∞).
Пример 12.
Разложить в ряд
Маклорена функцию
![]() ,
используя стандартные разложения
элементарных функций в ряд.
,
используя стандартные разложения
элементарных функций в ряд.
Решение.
Так как
![]()
то, заменяя в этом
равенстве x
на
![]() ,
будем иметь
,
будем иметь
![]()
поэтому
![]()
Пример 13.
Разложить в ряд
Тейлора функцию
![]() по степеням x–1.
по степеням x–1.
Решение.
Разложение функции по степеням x–1 означает, что в разложении в Ряд Тейлора a=1.
Преобразуем данную
функцию так, чтобы можно было использовать
разложение функции
![]() .
.
Полагая
![]()
из тождества
![]() найдем
найдем
![]()
следовательно,
 .
.
Заменив x
в разложении функции
через
![]() ,
получим
,
получим

Это разложение справедливо, когда
![]() .
.
Задание 631-640.
Пример 14.
Вычислить
 с точностью до 0,001.
с точностью до 0,001.
Решение.
Разложение подынтегральной функции в степенной ряд имеет вид
![]()
Интегрируя этот ряд почленно, получим

Полученный числовой ряд – ряд Лейбница. Погрешность от отбрасывания всех членов, начиная с четвертого, будет по абсолютной величине меньше четвертого члена
![]() .
.
Вычисляя с точностью до 0,001, найдем

III. Задания к контрольной работе.
Задание 591-600.
Исследовать
сходимость числового ряда
![]() .
.
591.
![]() 592.
592.
![]()
593.
![]() 594.
594.
![]()
595.
![]() 596.
596.
![]()
597.
![]() 598.
598.
![]()
599.
![]() 600.
600.
![]()
Задание 601-610.
Определить, абсолютно или условно сходится ряд .
601.
![]() 602.
602.
![]()
603.
![]() 604.
604.
![]()
605.
![]() 606.
606.
![]()
607.
![]() 608.
608.
![]()
609.
![]() 610.
610.
![]()
Задание 611-620.
Найти интервал
сходимости степенного ряда
![]() и
исследовать
поведение
ряда на концах интервала.
и
исследовать
поведение
ряда на концах интервала.
611.
![]() 612.
612.
![]()
613.
![]() 614.
614.
![]()
615.
![]() 616.
616.
![]()
617.
![]() 618.
618.
![]()
619.
![]() 620.
620.
![]()
Задание 621-630.
Разложить функцию
![]() в ряд Тейлора по степеням (x-a).
в ряд Тейлора по степеням (x-a).
621.
![]() 622.
622.
![]()
623.
![]() 624.
624.
![]()
625.
![]() 626.
626.
![]()
627.
![]() 628.
628.
![]()
629.
![]() 630.
630.
![]()
Задание 631-640.
Вычислить определенный интеграл с точностью до 0,0001, разложив подынтегральную функцию в степенной ряд.
631.
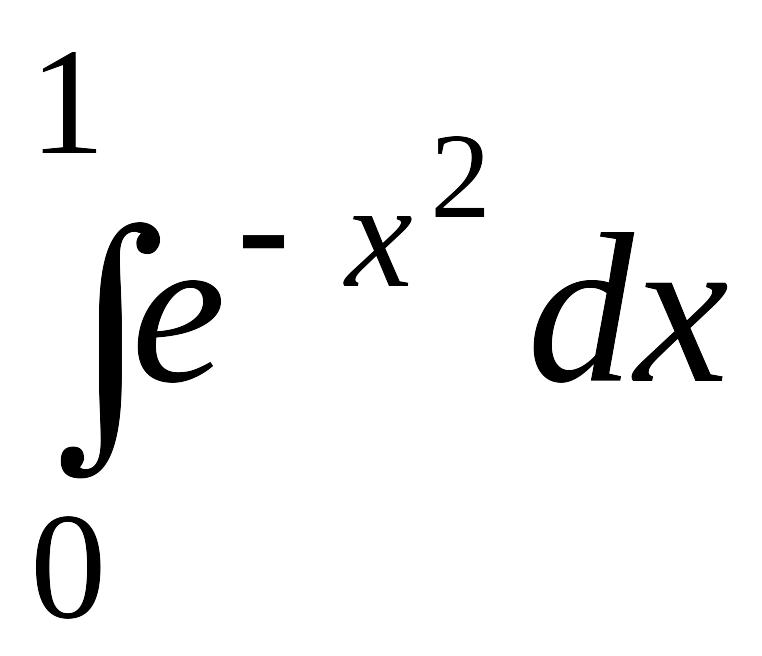 632.
632.
![]()
633.
![]() 634.
634.
![]()
635.
![]() 636.
636.
![]()
637.
 638.
638.
![]()
639.
![]() 640.
640.
![]()
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. т.I,II,М: Наука, 1985.
2.Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов, ч.1,2, М: Наука, 1993.
3.Данко П.Е. и др. Высшая математика в упражнениях и задачах. М: Высшая школа, 1999.
Учебное издание
Спиридонов Евгений Игоревич
РЯДЫ. Контрольная работа № 8
Учебно-методическое пособие
Компьютерная верстка
Редакция авторская
План 2005г. №
__________________________________________________________________
Формат 60х84 1/16 Бумага для множ. апп.
Печать офсетная
Усл.печ.л. 0,8 Усл.изд.л. 0,8 Тираж
Петербургский государственный университет путей сообщения.
190031, Санкт-Петербург, Московский пр., д.9.
