
5. Расчет наклонных сечений на действие изгибающего момента.
Обрыв продольной арматуры в пролете и построение эпюры материалов.
Расчет наклонных сечений на действие изгибающего момента заключается в проверке условия прочности (10.3) в соответствии с расчетной схемой по рис. 63:
,
или в виде (10.4)
![]()
При
отсутствии отгибов (![]() =
0) и замене по (10.11) сосредоточенных усилий
в хомутах непрерывно распределенными
(
=
0) и замене по (10.11) сосредоточенных усилий
в хомутах непрерывно распределенными
(![]() =
=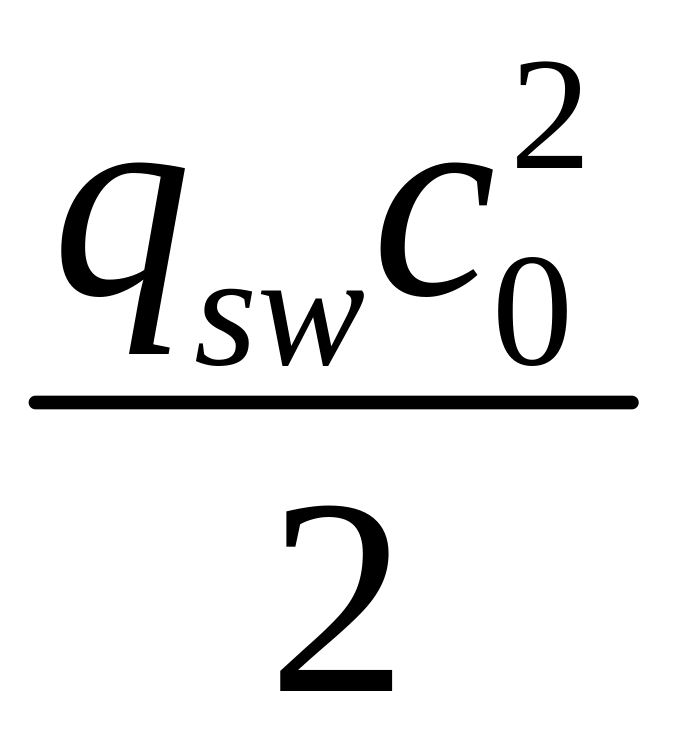 )
условие прочности примет вид
)
условие прочности примет вид
![]() (10.20)
(10.20)
где
![]() - расстояние от усилия в продольной
растянутой арматуре
- расстояние от усилия в продольной
растянутой арматуре
![]() до равнодействующей
до равнодействующей
![]() в сжатом бетоне (см. рис. 63); здесь
- высота сжатой зоны бетона над вершиной
наклонной трещины, определяемая из
условия равновесия
в сжатом бетоне (см. рис. 63); здесь
- высота сжатой зоны бетона над вершиной
наклонной трещины, определяемая из
условия равновесия
![]()
 ;
(10.21)
;
(10.21)
При
действии на элемент равномерно
распределенной нагрузки
![]()
 ,
(10.22)
,
(10.22)
здесь
![]() - поперечная сила в опорном сечении.
- поперечная сила в опорном сечении.
Как уже отмечалось в п. 3, расчет наклонных сечений на действие изгибающего момента не производят, если выполнены все конструктивные требования, которые состоят в следующем.
1.
Все стержни продольной арматуры доведены
до опор и надежно заанкерены (для свободно
опертых плит и балок растянутая арматура
заводится за внутреннюю грань опоры на
длину
![]() либо к концам стержней привариваются
анкера - см. лекция № 5 п.2).
либо к концам стержней привариваются
анкера - см. лекция № 5 п.2).
2. Обрываемая в пролете часть продольной арматуры должна быть заведена за место теоретического обрыва (м.т.о) на величину
 , (10.23)
, (10.23)
где
-
поперечная сила в нормальном сечении,
проходящем через точку теоретического
обрыва стержней;
![]() - усилие в хомутах на рассматриваемом
участке длиной
- усилие в хомутах на рассматриваемом
участке длиной
![]() ,
кН/м;
,
кН/м;
![]() - диаметр обрываемых стержней.
- диаметр обрываемых стержней.
Пояснения по поводу обрыва продольной
арматуры. Для экономии стали часть
продольной арматуры (не более 50% от
расчетной площади сечения
![]() )
можно не доводить до опор, а обрывать в
пролете там, где она уже не требуется
согласно расчету прочности по нормальным
сечениям. В балках шириной более 150 мм
до опор доводят не менее 2-х стержней;
при ширине сечения 150 мм и менее (ребра
сборных панелей и т.п.) допускается
доводить до опор один стержень.
)
можно не доводить до опор, а обрывать в
пролете там, где она уже не требуется
согласно расчету прочности по нормальным
сечениям. В балках шириной более 150 мм
до опор доводят не менее 2-х стержней;
при ширине сечения 150 мм и менее (ребра
сборных панелей и т.п.) допускается
доводить до опор один стержень.
Для определения м.т.о. строят так называемую эпюру материалов (арматуры) в такой последовательности.
1. В определенном масштабе строится эпюра изгибающих моментов от внешней нагрузки.
2.
Определяется момент
![]() ,
воспринимаемый нормальным сечением
элемента при полном количестве арматуры
(например, по рис. 67 полное количество
растянутой арматуры – это 220+216)
,
воспринимаемый нормальным сечением
элемента при полном количестве арматуры
(например, по рис. 67 полное количество
растянутой арматуры – это 220+216)
![]() ;
;
![]() ;
;
 .
.
3. Ордината накладывается на эпюру изгибающих моментов в том же масштабе и через ее конец проводится горизонтальная линия.
4.
Намечается количество обрываемых
стержней (например, по рис. 67 – это 216)
и определяется по вышеприведенным
формулам момент
![]() ,
воспринимаемый нормальным сечением
элемента с тем количеством арматуры,
которое доводится до опор без обрыва
(по рис. 67 – это 220).
,
воспринимаемый нормальным сечением
элемента с тем количеством арматуры,
которое доводится до опор без обрыва
(по рис. 67 – это 220).
5. Ордината накладывается на эпюру изгибающих моментов в том же масштабе и через ее конец проводится горизонтальная линия. Точки пересечения этой линии с эпюрой изгибающих моментов (сечение I-I) и будут точками теоретического обрыва стержней (м.т.о).
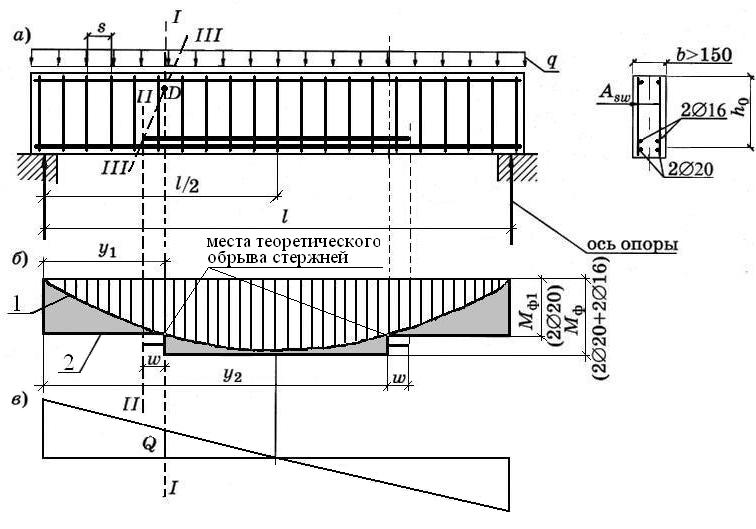
Рис. 67. Определение мест теоретического обрыва стержней в пролете:
а – схема армирования балки; б – эпюра моментов; в – эпюра поперечных сил;
I-I – нормальное сечение в месте обрыва стержней верхнего ряда; II-II – нормальное сечение
в месте их фактического обрыва; III-III – наклонное сечение, проходящее через точку D;
1 – эпюра расчетных моментов от нагрузки; 2 – эпюра моментов, воспринимаемых
нормальными сечениями балки (эпюра материалов)
6. Длину заделки обрываемых стержней за м.т.о определяют по формуле (10.23) из условия равнопрочности нормального сечения I-I, проведенного через м.т.о, и невыгоднейшего наклонного III-III.
При равномерно распределенной нагрузке на элемент точки теоретического обрыва стержней можно найти и аналитически из равенства внешнего и внутреннего моментов по уравнению (для свободно опертой балки)
 ,
,
где
- расчетная равномерно распределенная
нагрузка на балку;
![]() и
и
![]() - искомые абсциссы точек теоретического
обрыва продольных стержней верхнего
ряда (см. рис. 67).
- искомые абсциссы точек теоретического
обрыва продольных стержней верхнего
ряда (см. рис. 67).
![]()
