В) Приклади розв’язування задач

Приклад 1. Розв’язати матричну гру геометричним способом.

	8	3	2	1	6	10
	7	2	1	–5	5	8
	2	1	9	13	4	3
	1	–3	–5	–8	4	5

Розв’язання. Спочатку перевіримо, чи має дана гра розв’язок в чистих стратегіях, для цього знаходимо.

Так, як , то гра не має розв’язку в чистих стратегіях, і ціна гри знаходиться в межах .

Спростимо матричну гру, помітивши, що кожний елемент рядка и менший відповідного елементу рядка , тому другий і четвертий рядок можна викреслити.

	8	3	2	1	6	10
	2	1	9	13	4	3

Далі помічаємо, що стратегія домінує стратегію , , , тобто перший, п’ятий та шостий стовпчики можна видалити. Остаточно отримуємо:

	3	2	1
	1	9	13

Таким чином, гра викресленням заздалегідь невигідних стратегій зведена до гри .

В площині змінних побудуємо графіки очікуваних середніх виграшів першого гравця (рис.1), який застосовує першу стратегію з ймовірністю , а третю стратегію з ймовірністю за умови, що другий гравець відповідає чистою стратегією :

.

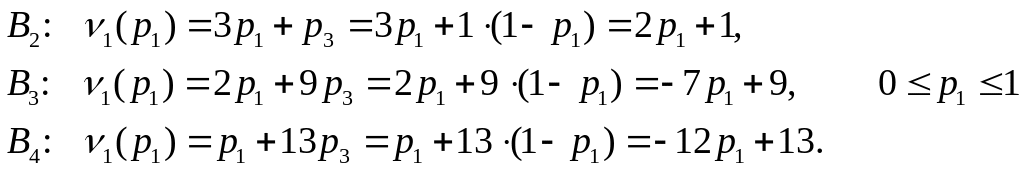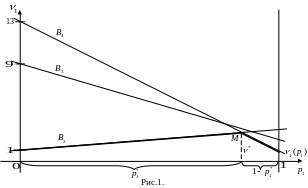
Нижня обвідна цього сімейства прямих на малюнку зображена жирною лінією. Найбільшого значення досягає в точці перетину прямих, які відповідають другій і четвертій чистій стратегії другого гравця.

Розв’язуючи систему: 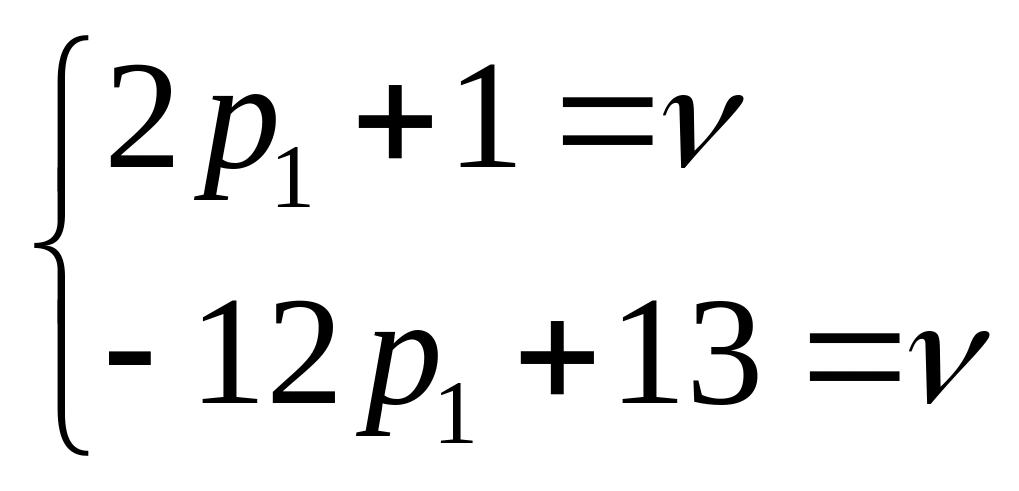, отримуємо . Так як стратегії та , являються заздалегідь невигідними стратегіями, тобто гравець ніколи не буде їх застосовувати в своїй оптимальній змішаній стратегії, тому ймовірність їх застосування відповідно буде дорівнювати нулю, . Отже,

Для знаходження оптимальної змішаної стратегії другого гравця враховуємо той факт, що , так як мінімальний гарантований програш другого гравця дорівнює і досягається на другій та четвертій чистих стратегіях. Прирівнюючи гарантований програш другого гравця значенню , отримуємо систему рівнянь для обчислення оптимальної змішаної стратегії другого гравця

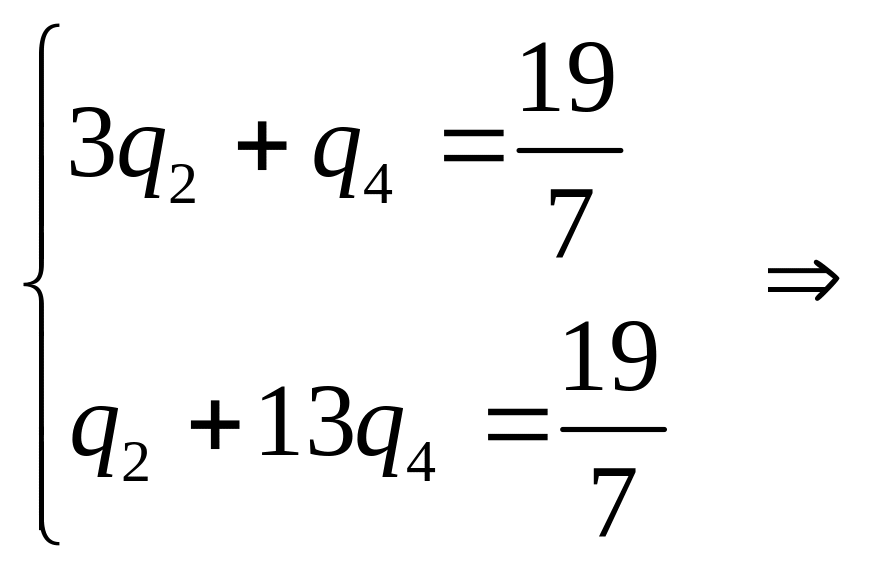
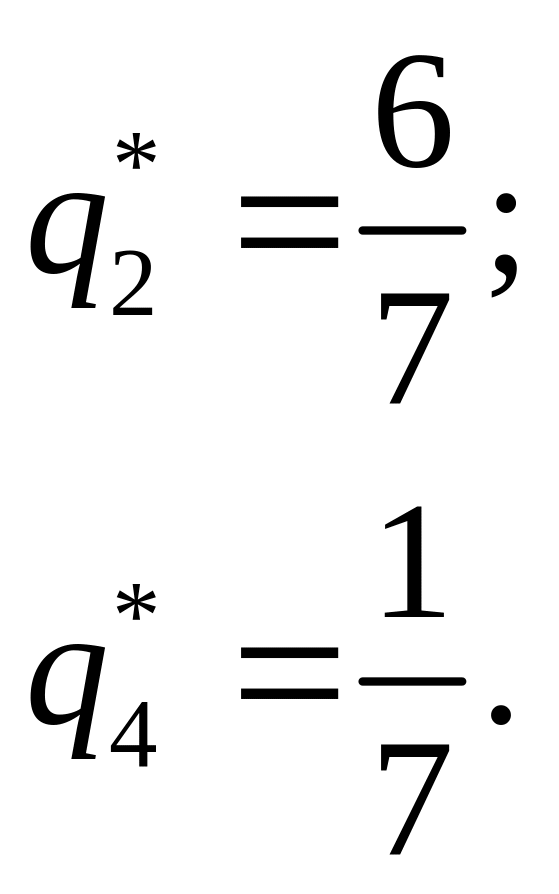
Отже,

Відповідь: ; ; .

Приклад 2. Розв’язати матричну гру геометричним способом.

	6	8	–3	0
	–3	4	5	8
	1	3	4	7
	5	9	1	3

Розв’язання. Гра не має розв’язку в чистих стратегіях, так як:

Так, як , то гра не має розв’язку в чистих стратегіях, і ціна гри знаходиться в межах .

Спростимо матричну гру, помітивши, що кожний елемент стовпчика більший відповідного елементу стовпчика , тому другий стовпчик можна викреслити. Далі помічаємо, що стратегія домінує стратегію , тобто четвертий стовпчик також можна видалити. Остаточно отримуємо:

	6	–3
	–3	5
	1	4
	5	1

Таким чином, гра викресленням заздалегідь невигідних стратегій зведена до гри .

В площині змінних побудуємо графіки очікуваних середніх програшів другого гравця (рис.2), який застосовує першу стратегію з ймовірністю , а третю стратегію з ймовірністю , за умови, що перший гравець відповідає чистою стратегією :

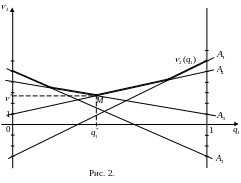
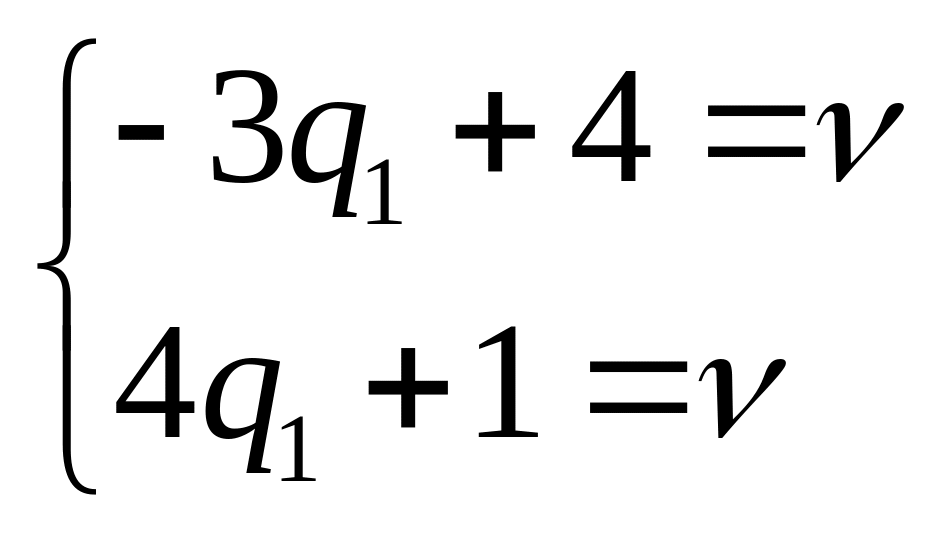Верхня обвідна цього сімейства прямих на малюнку зображена жирною лінією. Найменшого значення досягає в точці перетину прямих, які відповідають третій і четвертій стратегії першого гравця. Розв’язуючи систему: , отримуємо . Так як стратегії та , являються заздалегідь невигідними стратегіями, тобто гравець ніколи не буде їх застосовувати в своїй оптимальній змішаній стратегії, тому ймовірність їх застосування відповідно буде дорівнювати нулю, . Отже,

Для знаходження оптимальної змішаної стратегії першого гравця враховуємо той факт, що , так як максимальне значення гарантованого виграшу дорівнює і досягається на третій та четвертій чистих стратегіях першого гравця отримуємо систему рівнянь для обчислення оптимальної змішаної стратегії першого гравця

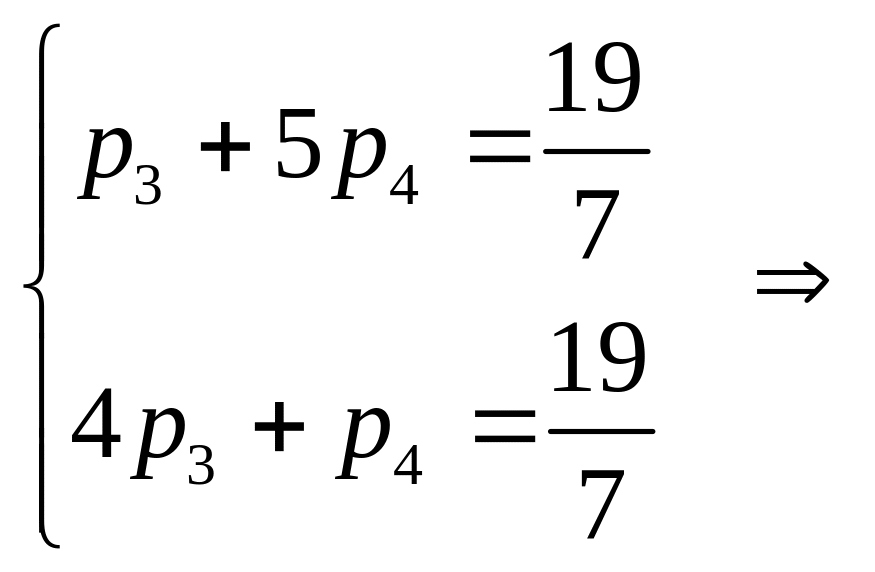
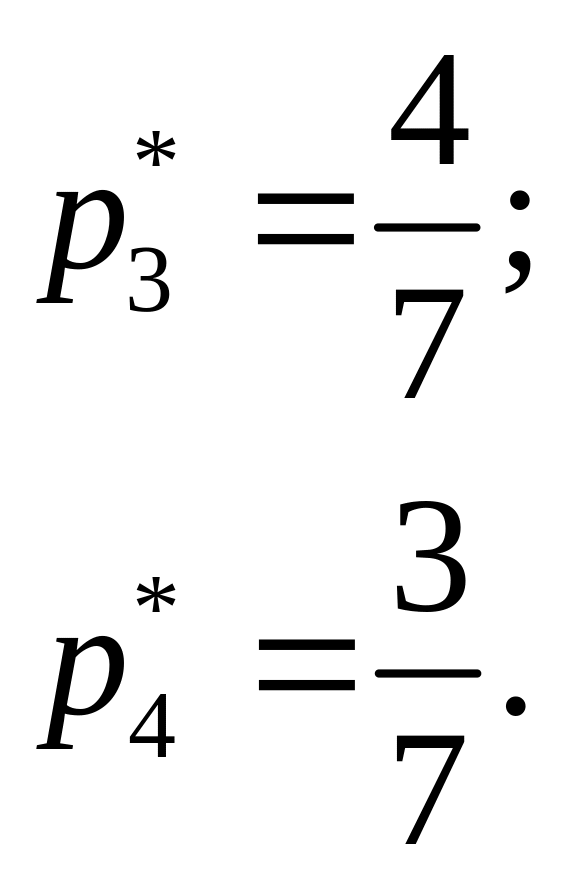
Отже,

Відповідь: ; ; .

Приклад 3. Розв’язати матричну гру геометричним способом.

	7	–3	0	1
	3	4	10	12
	2	3	–4	5
	8	4	3	2

Розв’язання. Спочатку перевіримо, чи має дана гра розв’язок в чистих стратегіях, для цього знаходимо:

Так як нижня ціна гри не дорівнює верхній, тобто , то дана гра не являється грою з сідловою точкою. Отже, для даної гри не існує розв’язку в чистих стратегіях. Тому будемо шукати розв’язок гри в змішаних стратегіях.

Спростимо матричну гру, помітивши, що стратегія домінує стратегії и , тому перший і третій рядки можна викреслити. Отримуємо матрицю:

	3	4	10	12
	8	4	3	2

Таким чином, гра викресленням заздалегідь невигідних стратегій зведена до гри .

В площині змінних побудуємо графіки очікуваних середніх виграшів першого гравця (рис.3), який застосовує другу стратегію з ймовірністю , а четверту стратегію з ймовірністю , за умови, що другий гравець відповідає чистою стратегією :

M

N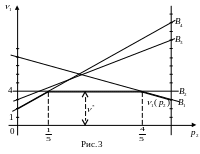

Нижня обвідна цього сімейства прямих на малюнку зображена жирною лінією, вона містить горизонтальний відрізок, тобто найбільше значення зображується відрізком , паралельним осі , який відповідає чистій стратегії гравця , яка і являється оптимальною для нього, ціна гри . Гравець в цьому випадку має нескінченно багато оптимальних змішаних стратегій: в оптимальній стратегії може змінюватися від до , тобто , , де ,

Відповідь: ; , ,