Лабораторна робота 11з. Дослідження залежності моменту інерції дволанкової системи від її геометричних параметрів

Завдання: експериментально дослідити залежність моменту інерції дволанкової системи від кута між її ланками.

Приладдя: штатив із горизонтальною віссю, на яку підвішують дволанкову систему; металева тригранна призма; технічні терези з набором різноважок; вимірна лінійка; секундомір; транспортир.

Теоретичний матеріал, який потрібно засвоїти під час підготовки до виконання роботи: центр мас; момент інерції матеріальної точки та твердого тіла; момент сили; момент імпульсу; рівняння моментів; фізичний маятник.

Література:

1. § 32-39, с.89-98; § 64, с.168-172.

2. § 4.1-4.6, с.52-68; § 4.4, с.59-62; § 4.6, с.66-68.

3. § 2.3, с.144-147; § 9.5, с.86-87.

4. § 4.1-4.3, с.86-96; § 10.5, с.220-223.

О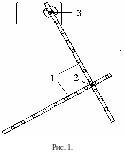 пис установки.

Основною частиною уста-новки є дволанкова система (рис. 1), що складається з двох металевих планок 1 із рівновіддаленими отворами. Пла-нки (ланки) можна жорстко скріпити гвинтом 2 у різних точках під довільним кутом. Якщо таку систему підвісити на горизонтальну вісь 3, яка не проходитиме через центр мас ланок і надати їй коливального руху, то вона буде коливатись як фізичний маятник.

Ідея роботи та виведення робочої формули.

Відомо, що період коливань фізичного маятника описує формула

, (1)

де І – момент інерції маятника, m – маса маятника; g – прискорення вільного падіння; d – відстань від центра мас маятника до осі підвісу.

З наведеної формули для моменту інерції одержимо

. (2)

Вірогідно, що в разі зміни кута розхилу між ланками змінюватиметься положення центра мас системи, тобто відстань d, що відповідно зумовить зміну моменту інерції системи І. Саме цю залежність моменту інерції дволанкової системи від кута між ланками і потрібно дослідити.

Порядок виконання роботи

1. Визначити масу першої m₁ i другої m₂ ланки (з гвинтом і гайкою).

2. З’єднати ланки (точку з’єднання задає викладач) так, щоб кут між ними дорівнював 0°, і визначити положення центра мас системи. Для цього жорстко з’єднану систему потрібно зрівноважити на ребрі тригранної призми. Визначити лінійкою відстань від положення центра мас до точки підвісу.

3. Підвісити систему на горизонтальну вісь так, щоб вісь пройшла через точку підвісу 1 і надати системі коливального руху. Секундоміром визначити час t для n повних коливань системи та визначити період коливань Т=t/n. Результати експерименту записати в таблицю.

4. Досліди пунктів 2 і 3 повторити для кута 180° між ланками.

5 . Для визначення відстані d за кутів 135° , 90° i 45° необхідно виконати геометричну побудову (див. рис. 2) на підставі таких вимірювань: а) методом, описаним у пункті 2, визначити положення центра мас ланок АВ i СД (точки А₁ і В₁) б) виміряти відстань А₁О=d₁ від центра мас першої ланки АВ до точки підвісу 0;

в) виміряти відстань В₁О₁=d₂ від центра мас другої ланки (разом з гвинтом і гайкою) до точки з’єднання ланок; г) на міліметровому папері виконати побудову згідно з рис. 2, де у довільно вибраному масштабі відкладені: АВ – довжина першої ланки, СД – довжина другої ланки розташованої під відповідним кутом ; точка О – точка підвісу, точка О₁ – точка з’єднання ланок, точка А₁ - положення центра мас першої ланки, точка В₁ – положення центра мас другої ланки. Центр мас дволанкової системи (точка О₂), вірогідно, лежить на лінії, яка з’єднує центри мас обох ланок (лінія А₁ В₁) і ділить відстань між ними на частини, які обернено пропорційні до мас ланок. Положення точки О₂ визначають так: із точки А₁ проводять у довільному масштабі та в довільному напрямі відрізок А₁А₂, пропорційний масі m₂ ланки СД, а з точки В₁ у протилежному напрямі в тому самому масштабі – відрізок В₁ В₂, пропорційний масі m₁ ланки АВ. Точка О₂ перетину прямих А₁В₁ i А₂В₂ i буде центром мас дволанкової системи.

6. Повторити дослід згідно з п. 2. для кутів, зазначених у п. 4.

7. Обчисліть момент інерції дволанкової системи для усіх значень кута та оцініть точність отриманих результатів.