§15. Деякі економічні задачі

• Задача міжгалузевого балансу

В деяких задачах макроекономіки ставиться питання про ефективне ведення багатогалузевого господарства. Тут кожна галузь є і виробником , і споживачем деякої продукції (як своєї, так і продукції, виробленої іншими галузями).

Однак, з економічної точки зору, міжгалузевий баланс є більш ефективним у вартісному виразі. При цьому об’єднання окремих галузей у підгрупи полегшує складання балансів продукції.

Введемо такі позначення:

x_i - загальна вартість продукції, виробленої в і-ій галузі (план валового випуску продукції) (i=1,2,…,n);

- вартість продукції ої галузі, необхідної для випуску

продукції го підрозділу ( ;

- вартість продукції ої галузі, призначеної для реалізації (кінцевий продукт).

Прямі витрати одиниць ої галузі, які використовуються для випуску одиниці виробу продукції ої галузі, а також кінцевий продукт задані таблицею:

Вартість продукції	Прямі витрати				Кінцевий продукт
	1	2	…
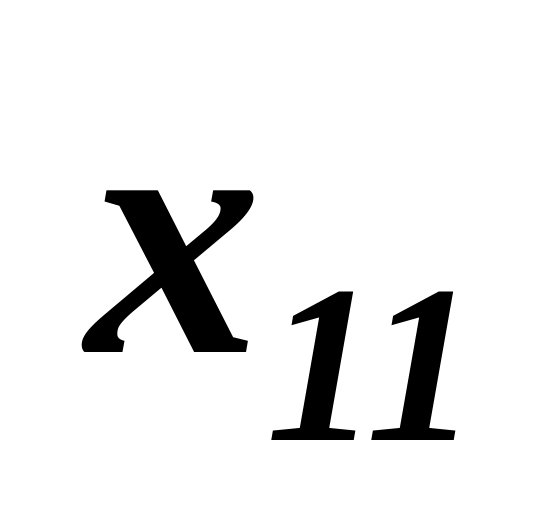
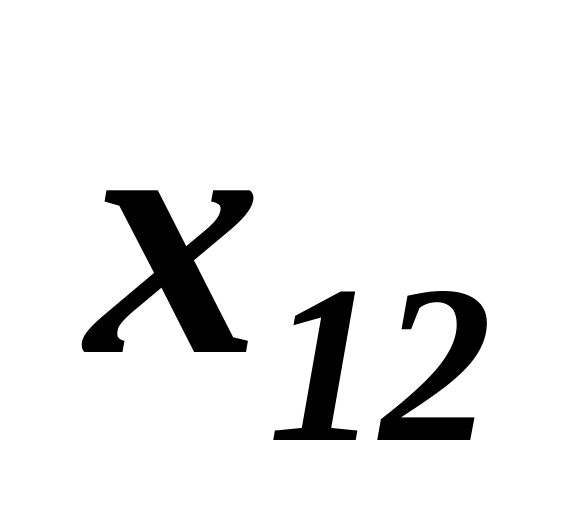
			…	X1n
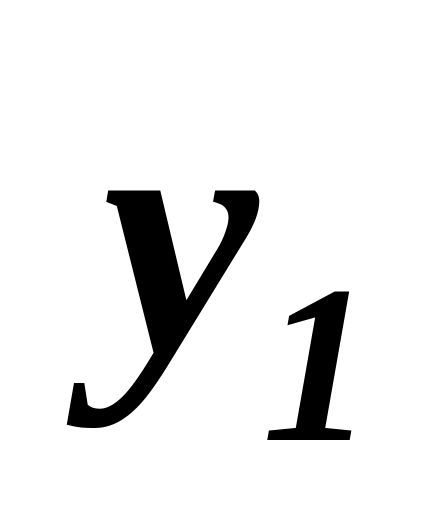
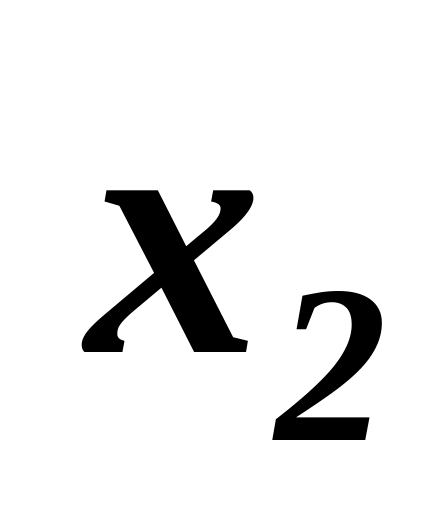
			…	X2n
…	…	…	…	…	…
	xn1	xn2	…	xnn

Зв’язок між цими величинами запишемо у вигляді системи рівнянь:

Рівняння цієї системи називаються балансовими.

Позначимо - вартість продукції ої галузі , необхідної для випуску одиниці продукції ої галузі:

.

Матриця, складена із величин

називається

матрицею прямих

витрат,

а її елементи – коефіцієнтами прямих витрат.

Враховуючи, що , вихідна система запишеться так:

або

Позначимо через

і назвемо вектор-планом а 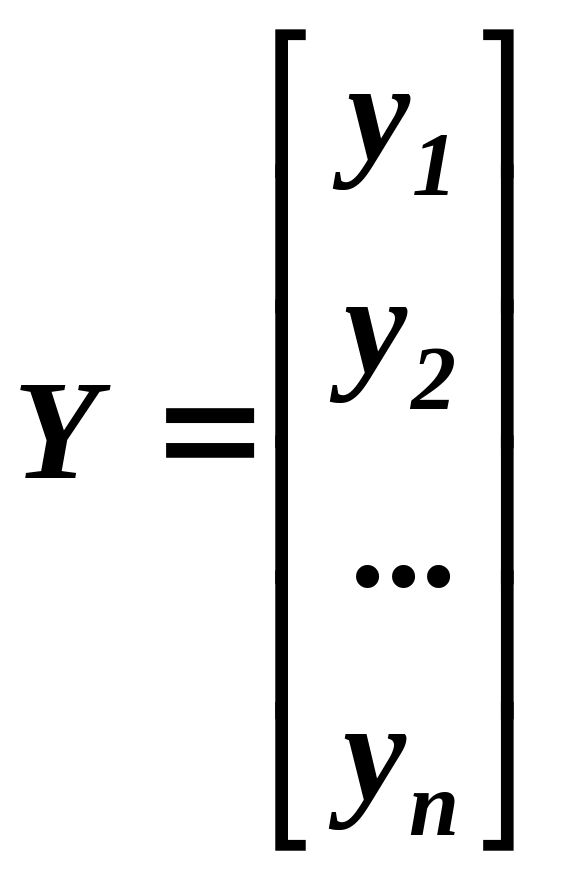і назвемо вектором кінцевих продуктів .

Попередня система запишеться у вигляді матричного рівняння , або , звідси ,

де - одинична матриця.

Позначимо , тоді система лінійних алгебраїчних рівнянь запишеться так

Помножимо з лівого боку обидві частини рівняння на : . Звідси .

Тобто вектор-план можна знайти, помноживши на вектор кінцевих продуктів.

Матриця називається матрицею повних витрат. Елементи цієї матриці включають прямі і непрямі витрати.

Задача 1. Прямі витрати трьох галузей виробництва, а також обсяги кінцевих продуктів ( у грошових одиницях) задані у таблиці:

Продукція цехів	Прямі витрати			Кінцевий продукт
	1	2	3
1	0,2	0,3	0,1	50
2	0,4	0,2	0,5	80
3	0,1	0,3	0,6	100

Потрібно знайти:

1. матрицю повних витрат;

2. план кожної галузі;

3. виробничу програму галузей;

4. коефіцієнти непрямих витрат.

Розв’язування. Із таблиці видно, що матриця прямих витрат буде: .

Позначимо через Х - вектор - план галузей виробництва, Y - вектор кінцевих продуктів:

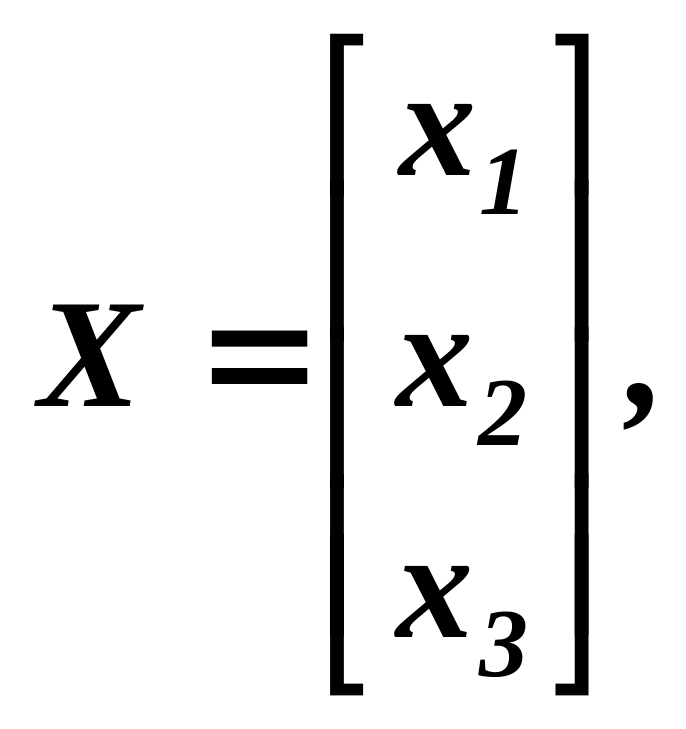
Зв’язок між величинами, записаних в таблиці представимо у вигляді системи лінійних рівнянь:

80