Теорема. Довільний вектор лінійного простору можна представити єдиним способом у вигляді лінійної комбінації векторів базису.

Доведення. Нехай базисом є система векторів -мірного простору Rⁿ. За означенням 4 довільні (n+1) вектори n-мірного простору Rⁿ лінійно залежні, а тому будуть лінійно залежними, зокрема, вектори і з вектором . Тобто

(2.28)

Тут , бо якби , то одне із чисел було б відмінним від нуля, а це означало б, що вектори є лінійно залежними, що суперечить умові теореми.

Тому що k≠0, то із рівності (2.28) маємо

(2.29)

Позначимо ( . Тоді рівність (2.29) перепишемо так

(2.30)

Значить вектор є лінійною комбінацією векторів базису.

Покажемо, що розклад (2.30) вектора є єдиний.

Припустимо, що існує інша лінійна комбінація, відмінна від (2.30), наприклад ,

(2.31)

Віднімаючи від рівності (2.30) рівність (2.31), одержимо

.

З цієї рівності і із лінійної незалежності векорів випливає, що або

Отже, розклад (2.28) є єдиний.

Числа називаються координатами вектора в базисі .

Нехай в просторі маємо два базиси , а саме старий і новий .

Нехай кожний вектор нового базису має в старому базисі координати , тобто

(2.32)

Матриця, виписана із коефіцієнтів системи (2.32) називається матрицею переходу від старого базису до нового.

Матриця - неособлива. Зворотній перехід від нового базису до старого здійснюється з допомогою оберненої матриці

Знайдемо залежність між координатами вектора в різних

базисах. Нехай вектор заданий в старому базисі, а

в новому базисі , тобто

. (2.33)

Так як вектор і один і той же вектор, то маємо

. (2.34)

Підставляючи в цю рівність розклад векторів по векторах , а саме (2.32) , то одержимо

.

З цієї рівності випливає зв’язок між координатами вектора в старому і новому базисах

. (2.35)

Якщо позначити , , то (2.35) запишеться так .

Таким чином, вектор в старих координатах дорівнює матриці переходу, помноженій на вектор в нових координатах.

Якщо матриця B невироджена, то , тобто одержи-

мо вектор в новому базисі через обернену матрицю переходу і координати вектора в старому базисі.

Приклад 1. Показати, що вектори

є лінійно незалежні.

Розв’язування. Складемо рівняння типу (2.26)

.

Цю рівність перепишемо у вигляді k₁(3;0;2)+k₂(1;-2;3)+k₃(1;4;5)=0.

Із даної рівності одержуємо систему лінійних рівнянь для знаходження :

Визначник цієї однорідної системи

.

Якщо то однорідна система має єдиний нульовий розв’язок Таким чином, дана система векторів лінійно незалежна.

Приклад 2. Задано вектори і в базисі Показати, що вектори утворюють базис і знайти координати вектора в цьому базисі.

Розв’язування. Покажемо, що вектори утворюють базис. Для цього складемо визначник із координат цих векторів.

Так як , то вектори утворюють базис. Виразимо зв’язок між базисами

.

Матриця переходу від базису до базису має вигляд

Знаходимо обернену матрицю до матриці .

, .

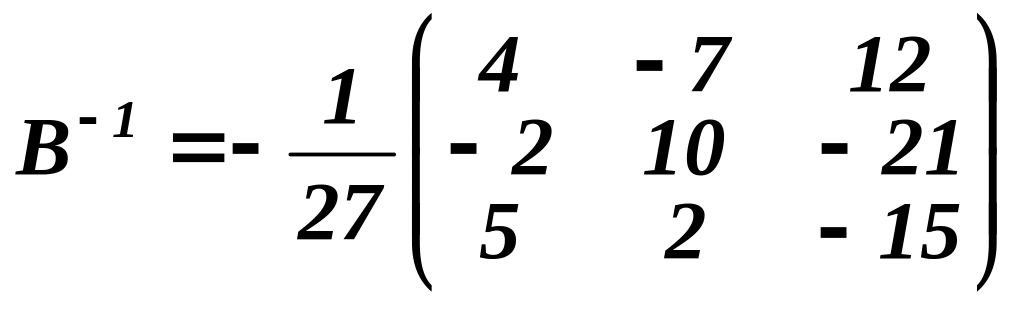Тепер

Нові координати вектора в базисі є –1;4;3. Вектор можна записати у вигляді

Примітка. Дану задачу можна розв’язати другим способом.

Для знаходження координат вектора в базисі складемо систему

Для знаходження розв’язків даної системи застосуємо правило Крамера.

.

,

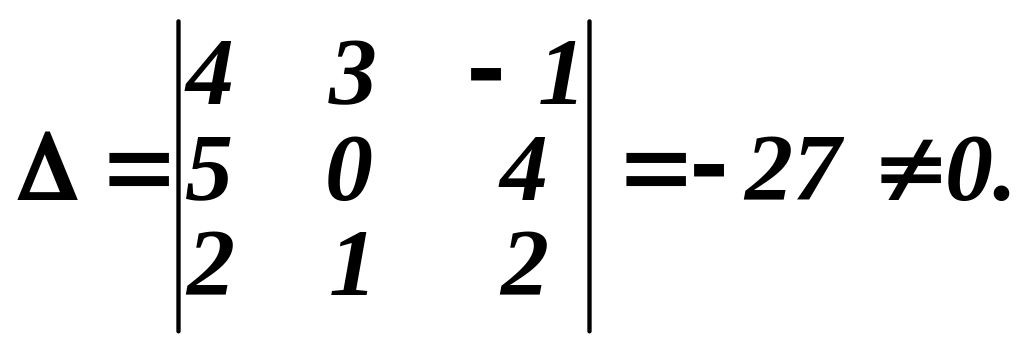
Значить вектор в базисі має координати