
5)
![]() ,
якщо
,
якщо
![]() і навпаки, якщо
,
то
.
і навпаки, якщо
,
то
.
Доведення.
За означенням скалярного добутку
![]() Якщо
Якщо
![]() ,
то вектори
,
то вектори
![]() перпендикулярні,
перпендикулярні,
![]() і
.Якщо
,
але
і
.Якщо
,
але
![]() ,
то
,
то
![]() ,
,
тобто вектори
,
,
тобто вектори
![]() і
і
![]() перпендикулярні.
перпендикулярні.
Скалярний добуток векторів в координатній формі.
Тому що одиничні
вектори (орти)
![]() осей
осей
![]() прямокутної системи координат взаємно
перпендикулярні, то на основі п’ятої
властивості скалярного добутку, маємо
прямокутної системи координат взаємно
перпендикулярні, то на основі п’ятої
властивості скалярного добутку, маємо
![]()
![]()
![]() (2.16)
(2.16)
Крім цього, за четвертою властивістю скалярного добутку
![]()
![]()
![]() (2.17)
(2.17)
Нехай задано два вектори з своїми координатами
![]()
![]()
![]()
Запишемо розклади цих векторів по ортам (формули 2.11)
![]()
![]()
Знайдемо скалярний добуток цих векторів
![]() .
.
Використовуючи формули (2.16), (2.17) знаходимо
![]() (2.18)
(2.18)
Таким чином, скалярний добуток двох векторів дорівнює сумі добутків однойменних координат цих векторів.
Якщо
![]() то
то
![]()
![]() ,
,
![]() При цьому отримаємо на основі рівності
(2.18), що
При цьому отримаємо на основі рівності
(2.18), що
![]() або
або
![]() (2.19)
(2.19)
Довжина вектора дорівнює квадратному кореню із суми квадратів його координат.
Із формули (2.12) знаходимо кут між двома векторами
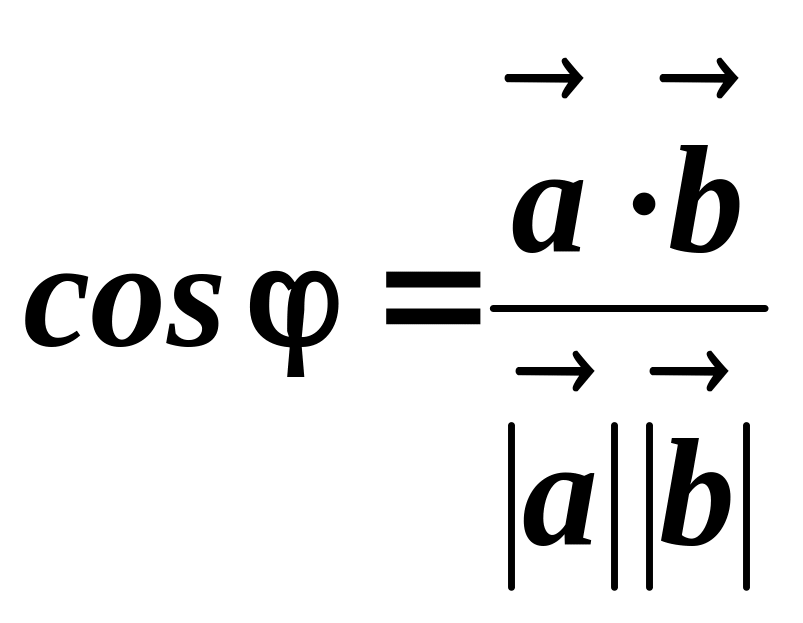 (2.20)
(2.20)
Формулу (2.20) на
основі формул (2.18) і (2.19) запишемо у
вигляді
![]() (2.21)
(2.21)
Якщо вектори
і
![]() є колінеарні, то вони задовольняють
умові (2.6) , а саме
є колінеарні, то вони задовольняють
умові (2.6) , а саме
![]() (2.22)
(2.22)
де скалярний
множник
![]() ,
коли вектори
і
мають одинаковий напрям, і λ<0
якщо протилежні напрями. Рівність (2.22)
в координатній формі запишеться так:
,
коли вектори
і
мають одинаковий напрям, і λ<0
якщо протилежні напрями. Рівність (2.22)
в координатній формі запишеться так:
![]() ,
,
![]() ,
,
![]() або
або
![]() (2.23)
(2.23)
Умова (2.23) є умовою паралельності векторів і .Отже, якщо вектори і колінеарні, то їх однойменні координати пропорціональні і навпаки.
Необхідною і
достатньою умовою перпендикулярності
векторів
і
є рівність
![]() або в координатній формі
або в координатній формі
![]() (2.24)
(2.24)
Умова (2.24) є умовою перпендикулярності двох векторів.
Приклад 1.Знайти
проекцію вектора
![]() на напрям вектора
на напрям вектора
![]()
Розв’язування. Із формули (2.14) одержимо
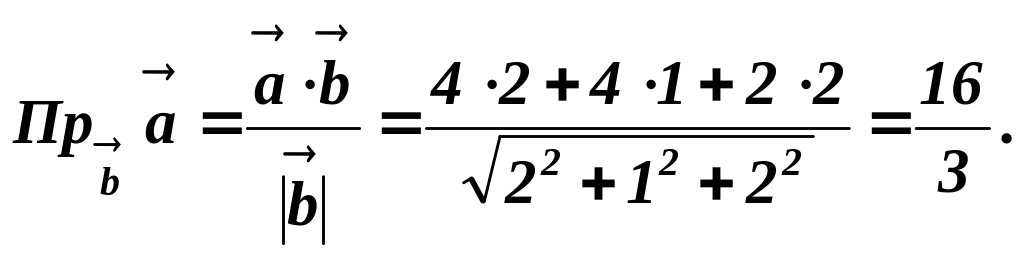
Приклад 2.
Виразити через орти![]() орт
орт
![]() вектора
вектора
![]() .
.
Розв’язування. Одиничний вектор

Приклад 3. Підприємство випускає продукцію чотирьо видів в кількості 210, 160, 172 і 300 штук. Ціни в одних і тих же грошових одиницях задані в такому порядку: 4,3;1,2;7;2,1. Обчислити сумарну ціну всієї продукції.
Розв’язування.
Запишимо дані про випуск продукції у
вигляді векторів
![]() ,
а також ціни одиниці кожної із виду
продукції
,
а також ціни одиниці кожної із виду
продукції
![]() .Тепер
сумарна ціна П
всієї
продукції запишеться на основі формули
2.18.
.Тепер
сумарна ціна П
всієї
продукції запишеться на основі формули
2.18.
![]() .
.
§12. n-мірний вектор і векторний простір
Множина всіх векторів, які ми розглядали на площині або в просторі і для яких визначені операції додавання векторів, множення вектора на число є простими прикладами векторного простору.
Означення 1.
Упорядкована множина n дійсних чисел,
записаних у вигляді
![]() називається n- мірним вектором. Числа
називається n- мірним вектором. Числа
![]() називаються координатами вектора
,
тобто
називаються координатами вектора
,
тобто
![]() .
.
Поняття n-мірного
вектора широко використовується в
економіці, наприклад, деякий набір
товарів можна охарактеризувати вектором
,
а відповідно ціни вектором
![]()
Якщо в n-мірного вектора одна координата дорівнює одиниці, а всі решту рівні нулю, то такий вектор називається одиничним. Очевидно, що існує n різних одиничних векторів
![]()
![]()
![]()
які виходять із початку координат точки О. Всі означення і дії для
двомірних і тримірних векторів, заданих в координатній формі, розповсюджуються і на n-мірні вектори (n≥4).
Два n-мірні вектори рівні тоді і тільки тоді, коли їх відповідні компоненти рівні.
Вектор
і вектор
![]()
рівні, коли ai=bi
(![]()
Сумою двох
n-мірних векторів
![]() і
є
третій n-мірний вектор
і
є
третій n-мірний вектор
![]() ,
координати якого дорівнюють сумі
відповідних однойменних координат
векторів
і
,
тобто
,
координати якого дорівнюють сумі
відповідних однойменних координат
векторів
і
,
тобто
![]() (
(
Добутком вектора
на дійсне число
![]() називається вектор
називається вектор
![]() ,
координати якого
,
координати якого
![]() дорівнюють добутку числа
на відповідні координати вектора
,
тобто
дорівнюють добутку числа
на відповідні координати вектора
,
тобто
![]() (
(
Вектор, у якого
всі координати дорівнюють нулю,
називається нульовим
вектором і
позначається
![]()
Операції над довільними векторами задовольняють властивостям:
 - переставний
закон;
- переставний
закон;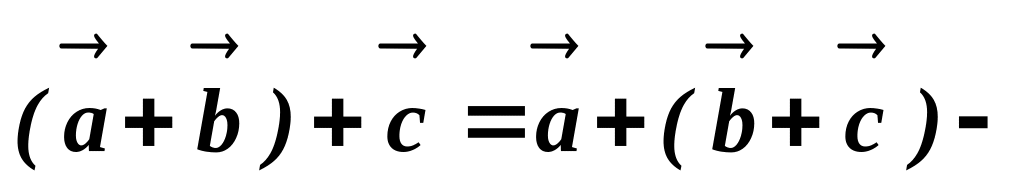 сполучний
закон;
сполучний
закон;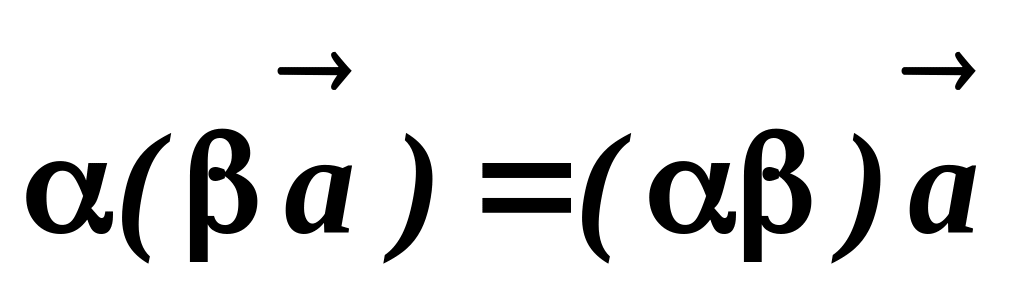 -
сполучний закон, відносно числового
множника;
-
сполучний закон, відносно числового
множника;(
 -
розподільчий закон відносно суми
векторів;
-
розподільчий закон відносно суми
векторів;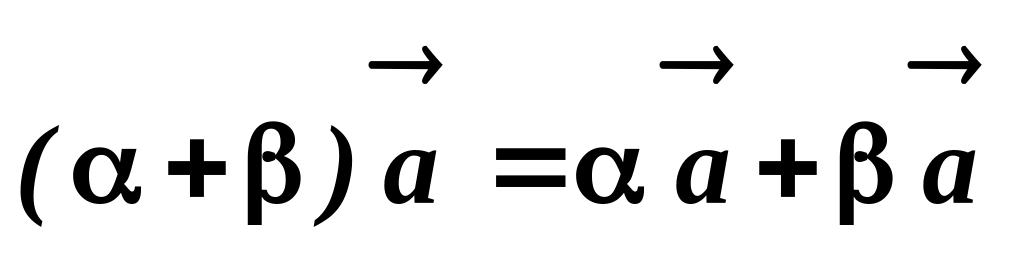 -
розподільчий закон відносно суми
числових множників.
-
розподільчий закон відносно суми
числових множників.Існує нульовий вектор
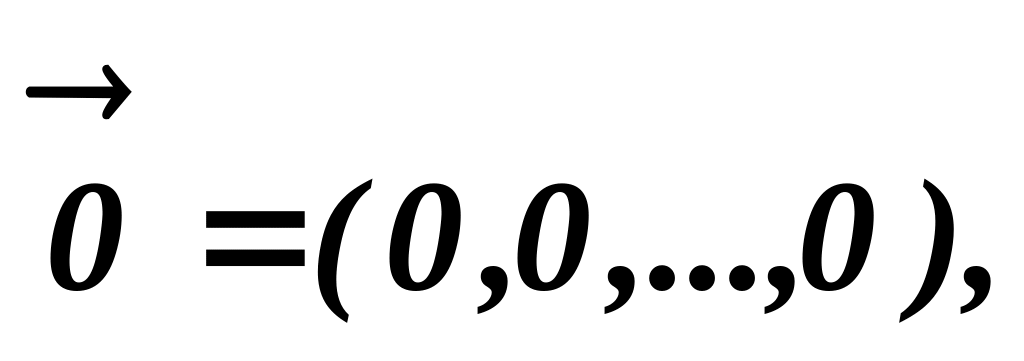 такий,що
такий,що
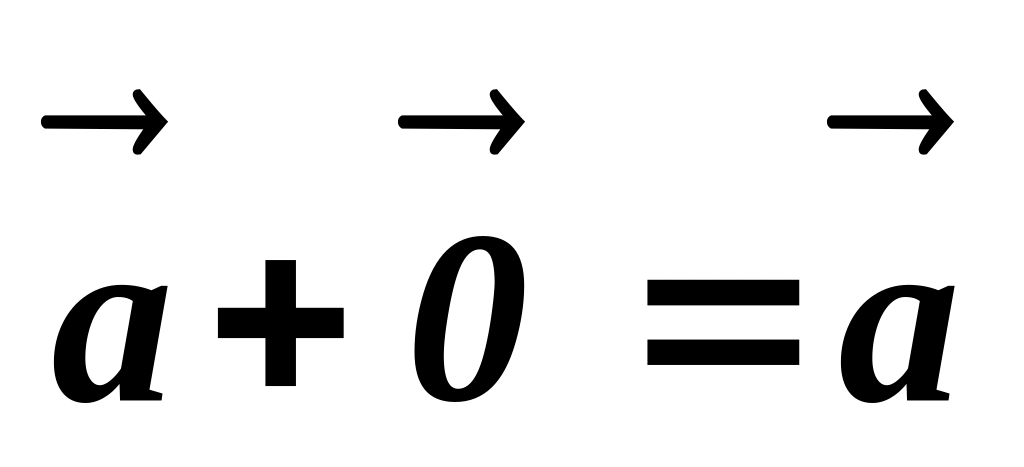 для довільного вектора
;
для довільного вектора
;Для довільного вектора існує протилежний вектор (- ), такий, що
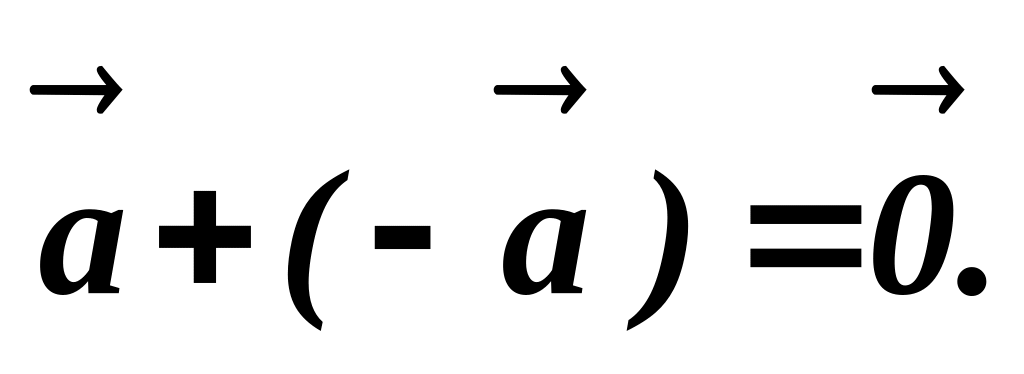
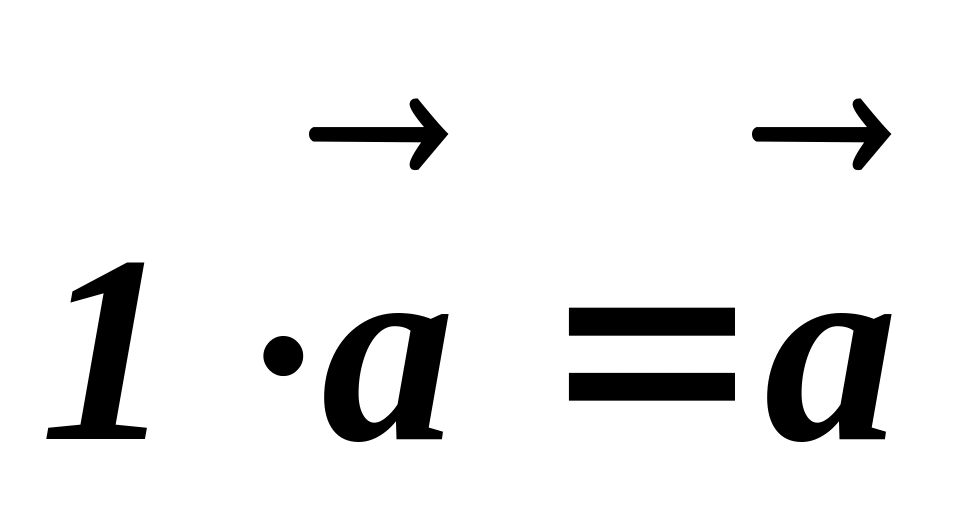 ,
для довільного вектора
(особлива роль числового множника 1).
,
для довільного вектора
(особлива роль числового множника 1).
Означення. Множина векторів з дійсними координатами, в якій визначено операції додавання векторів і множення вектора на число, які задовольняють вище приведеним восьми властивостям називається векторним простором.
Зауваження.
Якщо під векторами
![]() можна
розглядати елементи довільної природи,
то відповідна множина елементів
називається лінійним простором.
можна
розглядати елементи довільної природи,
то відповідна множина елементів
називається лінійним простором.
Лінійним простором
є, наприклад, множина всіх алгебраїчних
многочленів степені яких не перевищують
натурального числа
![]() .
Якщо множина всіх многочленів точно
дорівнює натуральному числу n,
то не буде лінійним простором тому, що
сума двох многочленів може виявитися
многочленом, степінь якого менше n.
.
Якщо множина всіх многочленів точно
дорівнює натуральному числу n,
то не буде лінійним простором тому, що
сума двох многочленів може виявитися
многочленом, степінь якого менше n.
§13. Базис. Розклад вектора по даному базису
Введемо поняття лінійної комбінації, лінійної залежності, а також базису і розклад вектора по базису.
Означення 1.
Вектор
називається
лінійною комбінацією векторів
![]() векторного
простору
векторного
простору
![]() якщо
він дорівнює сумі добутків цих векторів
на довільні дійсні числа
якщо
він дорівнює сумі добутків цих векторів
на довільні дійсні числа
![]() (2.25)
(2.25)
де
![]() - дійсні числа.
- дійсні числа.
Означення 2. Вектори називаються лінійно залежними, якщо існують такі числа , які не дорівнюють одночасно нулю, що
![]() (2.26)
(2.26)
Означення 3. Вектори називаються лінійно незалежними, якщо для них виконується умова (2.26) тільки тоді, коли одночасно дорівнюють нулю.
Розглянемо деякі властивості векторів лінійного простору.
Властивість 1. Якщо система векторів складається із одного
ненульового вектора , то така система лінійно незалежна.
Дійсно, рівність
![]() можлива тоді і тільки тоді, коли
можлива тоді і тільки тоді, коли
![]()
Зауваження. Якщо система векторів складається із одного нульового вектора , то ця система лінійно залежна.
Дійсно, рівність
має місце коли
![]()
Властивість 2 .Для того, щоб вектори були лінійно залежними необхідно і достатньо, щоб хоч один із них був лінійною комбінацією решти векторів.
Доведення. Необхідність.
Нехай вектори лінійно залежні. Тоді для них виконується умова (2.26), де хоч одне із чисел не дорівнює нулю.
Для прикладу, нехай
це буде число
![]() .
Тоді
.
Тоді
![]() (2.27)
(2.27)
Необхідна умова доведена.
Достатність.Нехай
виконується умова (2.27), яку перепишемо
так
![]() ,
де
,
де
![]()
Ми одержали рівність
вигляду (2.26), в якій одне число
![]() Значить вектори є лінійно залежні.
Значить вектори є лінійно залежні.
Властивість 3. Якщо серед векторів є нульовий вектор, то ці вектори є лінійно залежні.
Дійсно, нехай
![]() ,
то тоді маємо рівність (2.26)
,
то тоді маємо рівність (2.26)
![]() коли
коли
![]()
![]() .
.
Властивість 4. Для того, щоб два вектори були лінійно залежними необхідно і достатньо, щоб вони були колінеарні.
Доведення.Необхідність.
Нехай два вектори
і
є
лінійно залежними, тоді виконується
рівність
![]()
де хоч би одне із
чисел
![]() або
або
![]() не
дорівнює нулю.
не
дорівнює нулю.
Нехай
![]() ,
тоді
,
тоді
![]() тобто
вектори
і
є колінеарними.
тобто
вектори
і
є колінеарними.
Достатність. Нехай вектори і колінеарні, тобто
![]() або
або
![]() .
.
Значить вектори і є лінійно залежні.
Властивість 5.
Вектори
![]() -мірного
простору лінійно незалежні, якщо
визначник складений із координат цих
векторів, відмінний від нуля.
-мірного
простору лінійно незалежні, якщо
визначник складений із координат цих
векторів, відмінний від нуля.
Доведення. Нехай вектори задані своїми координатами
![]() ,
,
![]() ,….
,….![]()
Для цих векторів запишемо рівність
![]() або
або
![]()
З цієї рівності
одержуємо однорідну систему рівнянь
для знаходження
![]()
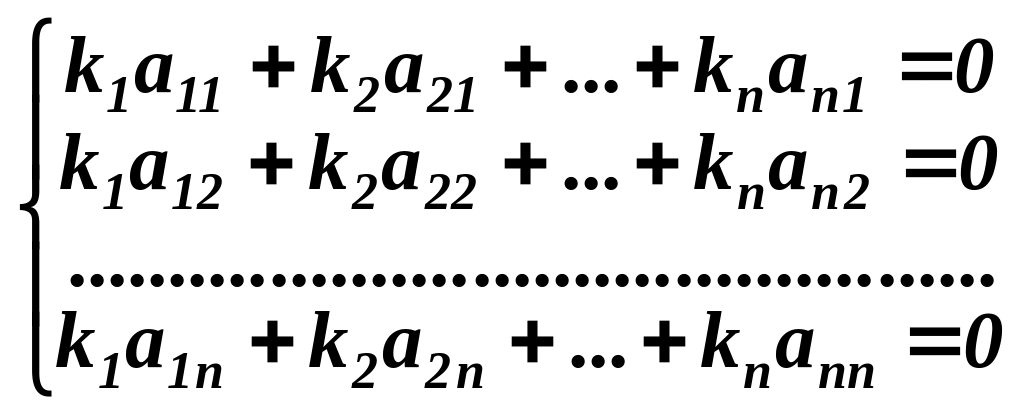
Тому що за умовою
визначник , складений із коефіцієнтів
цієї однорідної системи відмінний від
нуля, то ця система має єдиний нульовий
розв’язок, тобто
![]() А це значить, що вектори
лінійно
незалежні.
А це значить, що вектори
лінійно
незалежні.
Наслідок 1. Якщо вектори лінійно залежні, то визначник, складений із координат цих векторів, дорівнює нулю.
Наслідок 2.
Одиничні вектори (орти)
![]() -мірного
простору лінійно незалежні.
-мірного
простору лінійно незалежні.
Означення 4.
Лінійний простір
![]() називається
-
мірним, якщо в ньому є
лінійно
незалежних векторів, а довільні
називається
-
мірним, якщо в ньому є
лінійно
незалежних векторів, а довільні
![]() вектори є уже лінійно залежні.
вектори є уже лінійно залежні.
Іншими словами розмірність простору – це максимальне число лінійно незалежних векторів цього простору.
Означення 5. Сукупність лінійно незалежних векторів - мірного простору називається базисом.
