
- •Лабораторная работа №1.3(а) определение модуля юнга по изгибу пластины
- •Краткая теория
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №2 определение момента инерции махового колеса и силы трения в опоре
- •Краткая теория
- •Порядок выполнения работы.
- •Контрольные вопросы
- •Литература
Лабораторная работа №1.3(а) определение модуля юнга по изгибу пластины
Цель работы: практическое изучение закона Гука.
Задача: определить практически модуль Юнга по изгибу стальной и бронзовой пластины.
Приборы и принадлежности: 1.Кронштейн с опорами
2.Скоба – 50г.
3.Часовой индикатор перемещений
4.Грузы: 10г – 1шт;
20г – 2шт;
50г. – 1шт
5.Стальная и бронзовая пластина
Краткая теория
Сила характеризует действие одного тела на другое. В результате этого воздействия тело может прийти в движение или деформироваться. Деформацией твердого тела называется изменение взаимного расположения частиц тела, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. возникновение напряжений. Деформируемыми являются все вещества.
Деформация может быть следствием теплового расширения, воздействия электрических и магнитных полей, а также внешних механических сил.
В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает. Различают несколько видов деформации: деформация одноосного растяжения, деформация всестороннего сжатия, деформация кручения, деформация сдвига, деформация изгиба.
Внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая силой упругости. Силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) тела и имеют электрическую природу.
Физическая
величина, численно равная упругой силе
![]() ,
приходящейся на единицу площади
,
приходящейся на единицу площади
![]() сечение тела, называется напряжением:
сечение тела, называется напряжением:
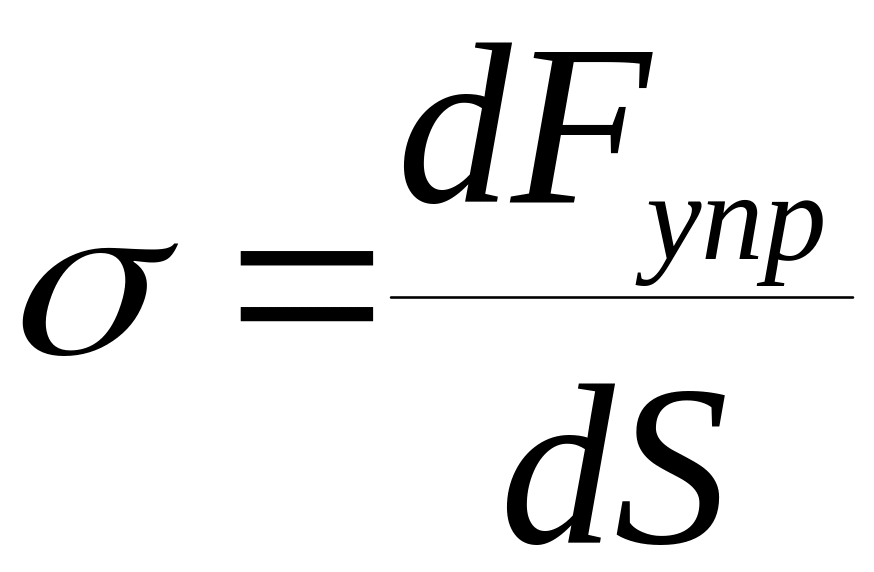
Английский
физик Р. Гук экспериментально установил,
что напряжение
![]() при упругих деформациях тела прямо
пропорционально его относительной
деформации
при упругих деформациях тела прямо
пропорционально его относительной
деформации
![]() :
:
![]() ,
(1)
,
(1)
где
![]() -
модуль Юнга (модуль упругости), величина
которого определяется свойствами
материала, из которого изготовлено
тело. Например,
-
модуль Юнга (модуль упругости), величина
которого определяется свойствами
материала, из которого изготовлено
тело. Например,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Относительная
деформация
равна отношению абсолютной деформации
![]() к
начальной длине
к
начальной длине
![]() :
:
 (2).
(2).
Рассмотрим упругую деформацию одностороннего растяжения .(рис. 1 )
К нижнему концу закрепленной проволоки
длиной
и площадью поперечного сечения
нижнему концу закрепленной проволоки
длиной
и площадью поперечного сечения
![]()
приложим
силу
![]() ,
под действием которой
,
под действием которой
проволока
получит абсолютное удлинение
![]()
и в ней возникнет сила упругости![]()
![]() .
.
По закону Гука напряжение , возникшее в
проволоке, прямо пропорционально относительной
деформации:
(1) ,
![]() отсюда модуль Юнга равен:
отсюда модуль Юнга равен:
Рис.
1 Е =
![]() (2)
(2)
Если
положить, что
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() ,
т.е. модуль
Юнга численно равен напряжению,
возникающему в упруго деформированном
теле, при относительной деформации,
равной единице.
,
т.е. модуль
Юнга численно равен напряжению,
возникающему в упруго деформированном
теле, при относительной деформации,
равной единице.
Заменив
в формуле (2) напряжение и относительное
удлинение по формулам
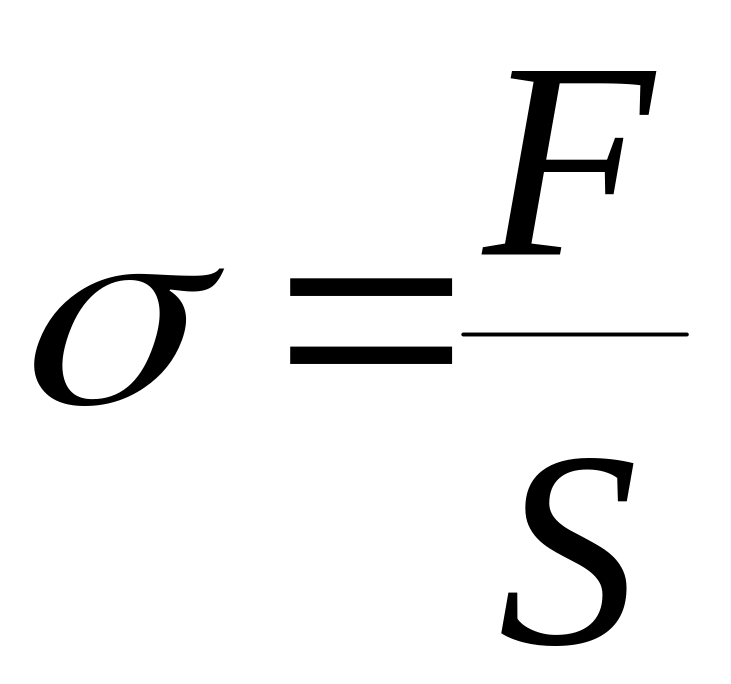 и
, получим:
и
, получим:
 (3)
(3)
Площадь
поперечного сечения проволоки
![]() (4), где
(4), где
![]() диаметр
проволоки.
диаметр
проволоки.
Несмотря на большое разнообразие способов деформирования твердых тел все виды деформаций можно свести к суперпозиции двух видов – деформации одноосного растяжения и сдвига. В частности при деформации изгиба пластины, лежащей свободно на двух опорах и нагружаемой в центре грузом, внутри деформируемого образца происходит одноосное растяжение слоев, величина которого определяется значением нагрузки и материалом этого образца. Расчеты показывают, что применительно к изгибу, как способу деформирования тела (см. рис. 2), представляющего собой пластину, модуль Юнга можно рассчитать по формуле:
![]() (4)
(4)
где F – нагрузка, вызывающая прогиб пластины, Н;
L =0,114 м – расстояние между призмами (опорами);
а = 0,012 м – ширина сечения пластины;
b =0,0008м – толщина пластины;
y = значение прогиба, м.
Нагрузка рассчитывается по формуле:
F=(mn-m1)g
где m1 – масса первого груза; mn – масса n-ного груза; g – ускорение свободного падения.
Значение прогиба у определяется по формуле:
у=уn-у1,
F
у









L

Рис.2
