
- •Розділ 5. Мікроекономічна модель підприємства
- •5.1. Модель діяльності підприємства з двофакторною виробничою функцією
- •Узагальнена модель діяльності підприємства
- •Види виробничих функцій (вф)
- •Кінцеві продукти ( ):
- •5.2. Основні поняття теорії виробництва для вф
- •Графічний спосіб представлення
- •Поняття теорії виробництва
- •Характеристики і
- •5.3. Класифікація виробничих функцій
- •5.4. Завдання до теми тести
- •1. Припустимо, що виробнича функція для товару задається функцією , де і - відповідні фактори капіталу і праці. Розгляньте 3 твердження щодо цієї функції:
Характеристики і
Графік |
Співвідношення та інтерпретація |
|||||||||||||||||||||||||
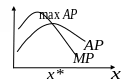
Рис. 5.3. Взаємозв’язок випуску продукції з граничною і середньою продуктивностями
|
ВФ у короткостроковому періоді: (рис. 5.3).
▪ При
обсязі
▪ При
обсязі
Зауваження.
Тангенс кута дотичної, проведеної до
ВФ, дорівнює граничній продуктивності
(
▪ При
обсязі
Коли
Коли
Коли , то випуск максимізується.
Необхідна
умова максимуму випуску:
Достатня
умова максимуму випуску:
|
|||||||||||||||||||||||||
|
Коли
Коли
Коли
Доведення
|
5.3. Класифікація виробничих функцій
Тепер розглянемо довгостроковий період, коли підприємство може змінювати всі фактори виробництва.
І. Лімітаційна (з факторами-досконалими доповнювачами) |
існують жорсткі співвідношення між обсягом ресурсів і величною продукції |
Приклад: складальні роботи, водій і транспортний засіб.
![]() ,
,
![]() ,
де
- велосипед,
- колеса,
- сидіння.
,
де
- велосипед,
- колеса,
- сидіння.
Звідси
![]() ,
,
![]() ,
тобто
,
тобто
![]() .
.
Висновок: для виготовлення одного велосипеду необхідно 2 колеса й одне сидіння. Якщо дане співвідношення не виконуватиметься, це означатиме, що один із ресурсів буде у надлишку, а інший – у дефіциті, що, зокрема, потребуватиме додаткових витрат на зберігання.
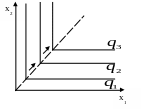
Ізокванти для досконалих доповнювачів (комплементів) представляють собою прямі кути і мають постійну пропорцію між обсягом ресурсів.
Рис.5.4. Лімітаційна ВФ (ВФ Леонтьєва)
ВФ:
|
Граничні
продуктивності
Точки, що не лежать у кутах ізоквант, є неефективними (витрати – вищі, а випуск – той же).
Гранична
норма технологічного заміщення
Еластичність
заміни
1) якщо
2) якщо
3)
якщо
|
ІІ. Субституційна (з факторами-досконалими замінниками) |
відсутні жорсткі технічні співвідношення між обсягом ресурсів і величною продукції, тобто певний обсяг продукцію можна виробити за допомогою різних ефективних комбінацій ресурсів. |
Приклад: покриття дороги асфальтом.
![]() ,
де
- кількість метрів дорожнього покриття,
- кількість машино-годин роботи
асфальтоукладальника,
- кількість людино-годин.
,
де
- кількість метрів дорожнього покриття,
- кількість машино-годин роботи
асфальтоукладальника,
- кількість людино-годин.
При
цьому 200 метрів дорожнього покриття
можна здійснити за допомогою 2 машино-годин
і 4 людино-годин
![]() або 1 машино-години і 12 людино-годин
або 1 машино-години і 12 людино-годин
![]() .
.
Висновок: на відміну від лімітаційної ВФ, для субституційної ВФ можна збільшити кількість продукції, збільшивши лише один фактор, коли решта факторів – постійні.
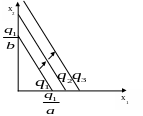
Ізокванти для факторів-досконалих замінників (субститутів) представлені прямими лініями.
Рис.5.5. Субституційна ВФ
ВФ:
|
Граничні
продуктивності
Для
даної ВФ властиве альтернативне
заміщення – один ресурс може бути
повністю заміщений іншим:
Гранична
норма технологічного заміщення
Еластичність
виробництва
Еластичність
заміни
Оскільки
При збільшенні на 1% відношення нескінченно зростає і навпаки. Дана ВФ рідко зустрічається на практиці – рис.5.5. |
ІІІ. Виробнича функція Кобба-Дугласа (ВФ К.-Д.) |
характеризує периферійне заміщення ресурсів – обсяги факторів виробництва залишаються у певних межах. |
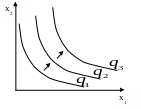
Ізокванти для ВФ К.-Д. представлені гіперболами.
Рис.5.6,а. ВФ Кобба-Дугласа
ВФ:
Степені і показують еластичність виробництва для ресурсів і відповідно.
Рис.5.6,б. ВФ Кобба-Дугласа зі змінним ефектом масштабу.
1.
2.
3.
|
1) якщо
2) якщо
3) якщо
ВФ К.-Д. є лінійною у логарифмічній формі:
▪ показує, на скільки процентів зміниться випуск продукції при зміні на 1%; ▪ показує, на скільки процентів зміниться випуск продукції при зміні на 1%. Зауваження. Економетрична оцінка параметрів і дозволяє визначити ефект масштабу ВФ К.-Д.
Граничні
продуктивності
Для
даної ВФ властиве периферійне
заміщення – один ресурс не може бути
повністю заміщений іншим. Якщо один
із ресурсів не використовується (
або
),
то
Гранична
норма технологічного заміщення
Еластичність
виробництва
,
,
де
Еластичність
заміни
Оскільки
Тож
При збільшенні на 1% відношення також зростатиме на 1% - рис.5.6(а). |
IV. CES - функція (ВФ з постійною еластичністю заміни) |
лінійно-однорідна ВФ з фіксованою еластичністю заміни ресурсів |
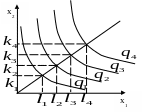
Ізокванти для CES – функції можуть бути представлені у формі прямого кута, прямої лінії, гіперболи.
Рис. 5.7. ВФ із постійною еластичністю заміни
ВФ:
|
1) якщо
2) якщо
3) якщо
Граничні
продуктивності
Для даної ВФ властиве альтернативне заміщення – один ресурс може бути повністю заміщений іншим.
Гранична
норма технологічного заміщення
Еластичність
виробництва
,
.
Тож
Еластичність
заміни
Оскільки
,
де
Тож
При
збільшенні
на 1% відношення
зростатиме на
|
Приклад. 5.1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Показник |
|
|
Граничний продукт |
|
|
Середній продукт |
|
|
Гранична
норма технологічного заміщення
|
|
|
Частинний
граничний продукт фактору
|
|
|
Загальний
граничний продукт
|
|
|
Еластичність
виробництва
|
|
|
Ефект масштабу |
Постійний ( )
|
Зростаючий
(
|
Еластичність заміни |
, . |
. |



 ,
,
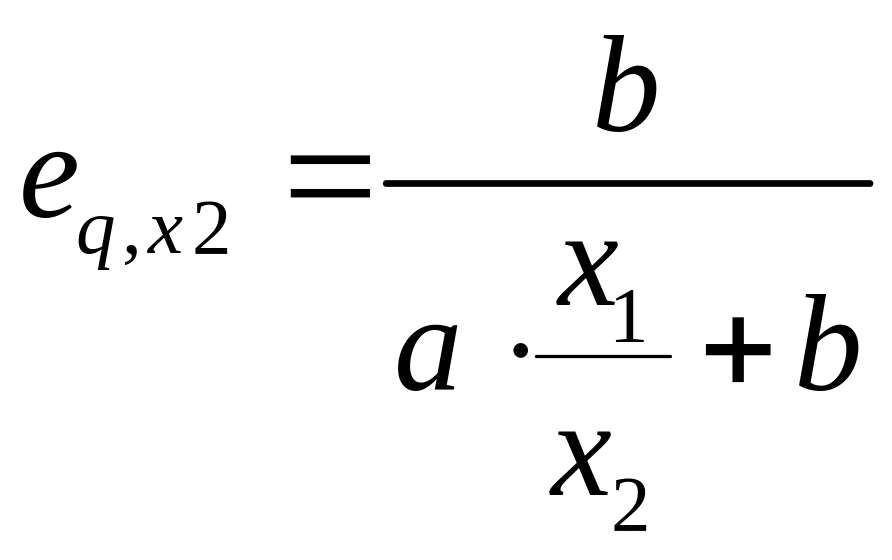 .
.
 - підприємство може відмовитися від
- підприємство може відмовитися від
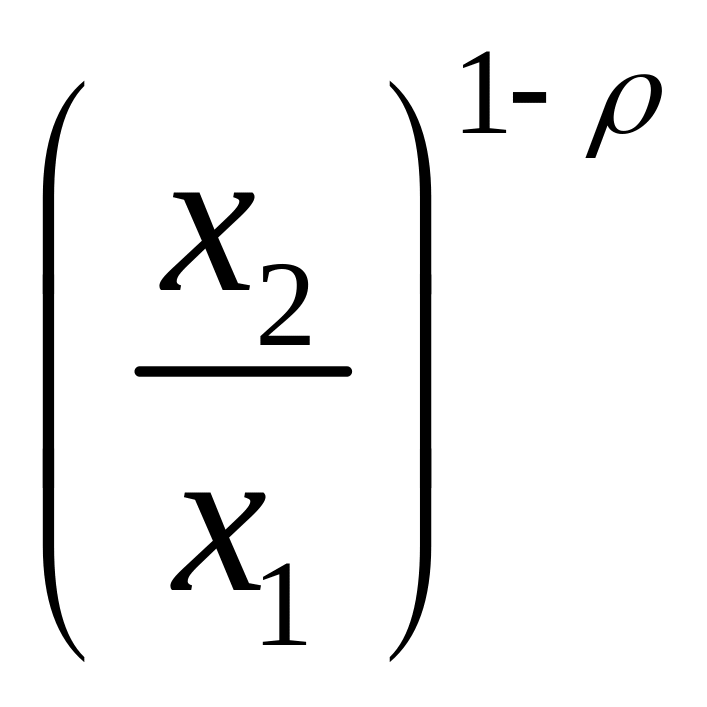 одиниць
в обмін на одиницю
без зміни обсягу виробництва
.
одиниць
в обмін на одиницю
без зміни обсягу виробництва
.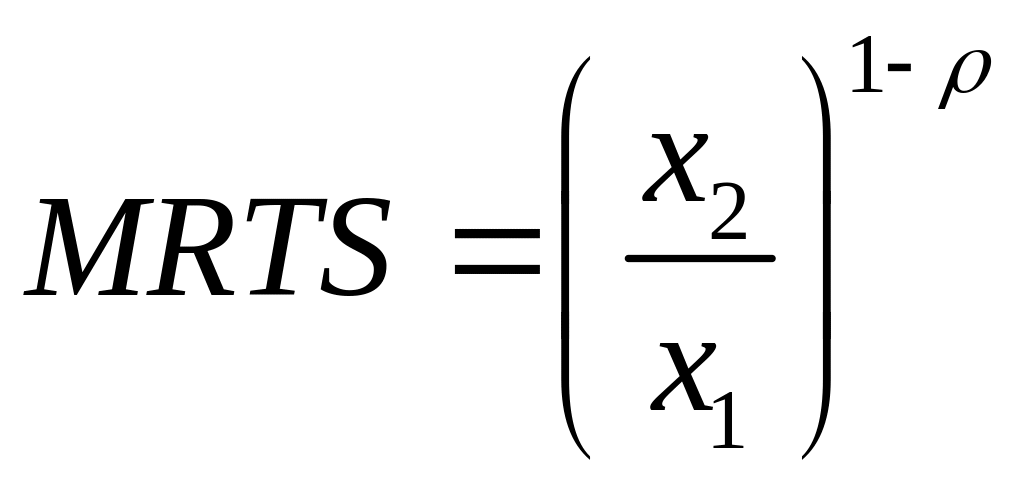 ,
звідки
,
звідки