В поле Ограничения введите все ограничения, накладываемые на поиск решения.

Добавление ограничений

1. В разделе Ограничения диалогового окна Поиск решения нажмите кнопку Параметры.

2. В поле Ссылка на ячейку введите адрес ячейки, на значение которой накладываются ограничения.

3. Выберите из раскрывающегося списка условный оператор ( <=, =, >=, цел или двоич ), который должен располагаться между ссылкой и ограничение. Если выбрано цел, в поле Ограничение появится «целое». Если выбрано двоич, в поле Ограничение появится «двоичное».

4. В поле Ограничение введите число, ссылку на ячейку или ее имя либо формулу.

5. Выполните одно из следующих действий.

   • Чтобы принять ограничение и приступить к вводу нового, нажмите кнопку Добавить.

   • Чтобы принять ограничение и вернуться в диалоговое окно Поиск решения, нажмите кнопку OK.

Примечания

• Условные операторы типа цел и двоич можно применять только при наложении ограничений на изменяемые ячейки.

• Флажок Линейная модель в диалоговом окне Параметры поиска решения позволяет задать любое количество ограничений. При решении нелинейных задач на значения изменяемых ячеек можно наложить более 100 ограничений, в дополнение к целочисленным ограничениям на переменные.

Изменение и удаление ограничений

1. В списке Ограничения диалогового окна Поиск решения укажите ограничение, которое требуется изменить или удалить.

2. Выберите команду Изменить и внесите изменения либо нажмите кнопку Удалить.

4. Нажмите кнопку Выполнить и выполните одно из следующих действий:

• чтобы сохранить найденное решение на листе, выберите в диалоговом окне Результаты поиска решения вариант Сохранить найденное решение;

• чтобы восстановить исходные данные, выберите вариант Восстановить исходные значения.

Просмотр промежуточных результатов поиска решения

1. В диалоговом окне Поиск решения нажмите кнопку Параметры.

2. Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры поиска решения установите флажок Показывать результаты итераций, а затем нажмите кнопку ОК.

3. В диалоговом окне Поиск решения нажмите кнопку Выполнить.

4. В диалоговом окне Текущее состояние поиска решения выполните одно из следующих действий.

• Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.

• Чтобы выполнить следующую итерацию и просмотреть ее результаты, нажмите кнопку Продолжить.

• Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Microsoft Excel будет пересчитан с учетом

Примечание

Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Microsoft Excel будет пересчитан с учетом найденных значений влияющих ячеек.

Разрешение вопросов, возникающих при поиске решения

а) Оптимальное решение не найдено.

Поиск решения может остановиться до достижения оптимального решения по следующим причинам.

• Был прерван процесс поиска.

• Команда Показывать результаты итераций в диалоговом окне Параметры поиска решения была выбрана до команды Выполнить.

• В режиме пошагового выполнения итераций по истечении времени, отведенного на работу процедуры, или после выполнения заданного числа итераций была нажата кнопка Стоп.

• Установлен флажок Линейная модель в диалоговом окне Параметры поиска решения, в то время как решаемая задача не линейна.

• Значение, заданное в поле Установить диалогового окна Поиск решения, неограниченно увеличивается или уменьшается.

• Необходимо изменить значения полей Максимальное время или Итерации в диалоговом окне Параметры поиска решения.

• В случае задач, значения в которых ограничены множеством целых чисел, необходимо уменьшить значение в поле Допустимое отклонение диалогового окна Параметры поиска решения, что позволит найти лучшее решение.

• В случае нелинейных задач необходимо уменьшить значение в поле Сходимость диалогового окна Параметры поиска решения, что позволит продолжать поиск решения, когда значение в целевой ячейке изменяется медленно.

• Необходимо установить флажок Автоматическое масштабирование в диалоговом окне Параметры поиска решения, если значения влияющих ячеек или значения влияющей и целевой ячеек различаются на несколько порядков.

После остановки на экране отображается диалоговое окно Результаты поиска решения. Установите переключатель в положение Сохранить найденное решение или Восстановить исходные значения, внесите нужные изменения и запустите процедуру поиска решения снова.

б) Значения влияющих ячеек и целевой ячейки или ячейки, на которую наложены ограничения, сильно различаются.

Если значения влияющих ячеек и целевых ячеек или ячеек, на которые наложены ограничения, различаются на несколько порядков, установите флажок Автоматическое масштабирование в диалоговом окне Параметры поиска решения. В случае нелинейных задач, прежде чем нажать кнопку Выполнить в диалоговом окне Поиск решения, убедитесь, что начальные значения во влияющих ячейках того же порядка, что и ожидаемые конечные значения.

в) Ожидаемое решение не получено.

Если найденное решение нелинейной задачи существенно отличается от ожидаемого результата, запустите процедуру поиска решения с другими начальными значениями влияющих ячеек. Если задать такие значения влияющих ячеек, которые расположены близко к экстремальной точке целевой функции, можно значительно сократить время поиска решения.

При решении линейных задач (то есть, если установлен флажок Линейная модель в диалоговом окне Параметры поиска решения) от начальных значений влияющих ячеек не зависят ни конечные значения, ни время поиска решения.

г) Найденное решение отличается от предыдущего результата.

Поиск решения отображает следующее сообщение: «Поиск свелся к текущему решению. Все ограничения выполнены.» Относительное изменение значения в целевой ячейке за последние пять итераций стало меньше установленного значения параметра Сходимость в диалоговом окне Параметры поиска решения. Чтобы найти более точное решение, установите меньшее значение параметра Сходимость, но это займет больше времени.

д) Поиск не может найти оптимальное решение

Далее приведен список итоговых сообщений процедуры поиска решения.

Поиск не может улучшить текущее решение. Все ограничения выполнены.

В процессе поиска решения нельзя найти такой набор значений влияющих ячеек, который был бы лучше текущего решения. Приблизительное решение найдено, но либо дальнейшее уточнение невозможно, либо погрешность, заданная в диалоговом окне Параметры поиска решения, слишком высока. Измените погрешность на меньшее число и запустите процедуру поиска решения снова.

Поиск остановлен (истекло заданное на поиск время).

Время, отпущенное на решение задачи, исчерпано, но достичь удовлетворительного решения не удалось. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное решение или Сохранить сценарий.

Поиск остановлен (достигнуто максимальное число итераций).

Произведено разрешенное число итераций, но достичь удовлетворительного решения не удалось. Увеличение числа итераций может помочь, однако следует рассмотреть результаты, чтобы понять причины остановки. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное решение или нажмите кнопку Сохранить сценарий.

Значения целевой ячейки не сходятся.

Значение целевой ячейки неограниченно увеличивается (или уменьшается), даже если все ограничения соблюдены. Возможно, следует в задаче снять одно ограничение или сразу несколько. Изучите процесс расхождения решения, проверьте ограничения и запустите задачу снова.

Поиск не может найти подходящего решения.

В процессе поиска решения нельзя сделать итерацию, которая удовлетворяла бы всем ограничениям при заданной точности. Вероятно, ограничения противоречивы. Исследуйте лист на предмет возможных ошибок в формулах ограничений или в выборе ограничений.

Поиск остановлен по требованию пользователя.

Нажата кнопка Стоп в диалоговом окне Текущее состояние поиска решения после прерывания поиска решения в процессе выполнения итераций.

Условия для линейной модели не выполняются.

Установлен флажок Линейная модель, однако итоговый пересчет порождает такие значения, которые не согласуются с линейной моделью. Это означает, что решение недействительно для данных формул листа. Чтобы проверить линейность задачи, установите флажок Автоматическое масштабирование и повторно запустите задачу. Если это сообщение опять появится на экране, снимите флажок Линейная модель и снова запустите задачу.

При поиске решения обнаружено ошибочное значение в целевой ячейке или в ячейке ограничения.

При пересчете значений ячеек обнаружена ошибка в одной формуле или в нескольких сразу. Найдите целевую ячейку или ячейку ограничения, порождающие ошибку, и измените их формулы так, чтобы они возвращали подходящее числовое значение.

Имя или формула в окне Добавить ограничение или в окне Изменить ограничение заданы неверно, либо в поле Ограничение было задано целое или двоичное ограничение. Чтобы ограничить значения ячейки множеством целых чисел, выберите оператор целого ограничения в списке условных операторов. Чтобы установить двоичное ограничение, выберите оператор для двоичного ограничения.

Мало памяти для решения задачи.

Система не смогла выделить память, необходимую для поиска решения. Закройте некоторые файлы или приложения и попытайтесь снова выполнить процедуру поиска решения.

Другой экземпляр Microsoft Excel использует SOLVER.DLL.

Запущено несколько копий Microsoft Excel, в одном из которых используется файл Solver.dll

2. Пример построения экономико-математических моделей задач

линейного программирования

Рассмотрим процесс построения математических моделей задач линейного программирования на примере определения оптимального ассортимента продукции.

Предприятие изготавливает два вида продукции – П₁ и П₂, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции вида П₁ и вида П₂ дан в таблице .

Таблица

Опыт работы показал, что суточный спрос на продукцию П₁ никогда не превышает спроса на продукцию П₂ больше, чем на 1 ед. Кроме того, известно, что спрос на продукцию П₂ никогда не превышает 2 ед. сутки.

Оптовые цены единицы продукции равны:

3 денежные единицы – для П₁;

4 денежные единицы – для П₂.

Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?

Решение.

Процесс построения математической модели для решения поставленной задачи начинается с ответов на следующие вопросы:

1. Для определения каких величин должна быть построена модель, т.е. как идентифицировать переменные данной задачи?

2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы?

3. В чем состоит цель задачи, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?

Ответы на вышеперечисленные вопросы могут быть сформулированы для данной задачи так:

Фирме требуется определить объемы производства каждого вида продукции в тоннах, максимизирующие доход в д.е. от реализации продукции с учетом ограничений на спрос и расход исходных продуктов.

Для построения математической модели необходимо идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.

Предположим, что предприятие изготовит х₁ единиц продукции вида П₁ и х₂ едини ц продукции вида П₂. Поскольку производство продукции П₁ и П₂ ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, должны выполняться следующие неравенства:

Доход от реализации х₁ единиц продукции П₁ и х₂ единиц продукции составит

Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.

Решим задачу линейного программирования с использованием функции «Поиск решения»

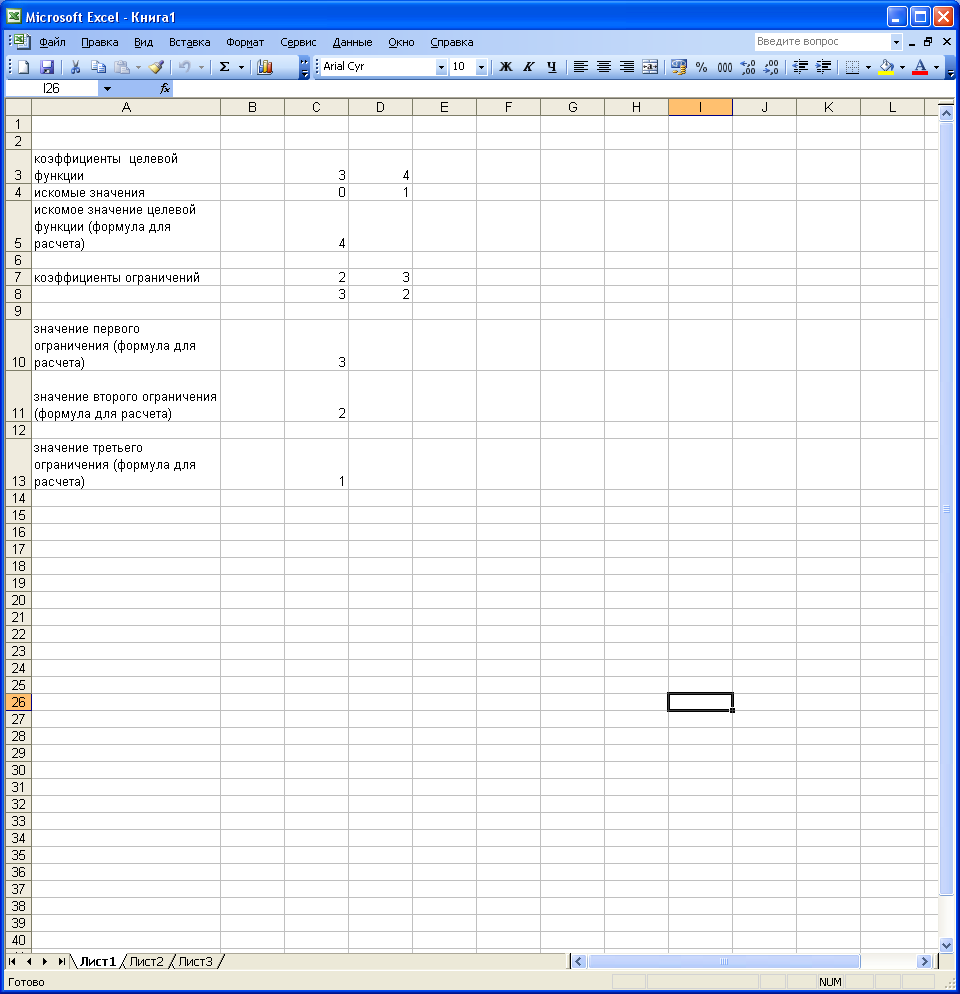
Исходные данные

Исходные данные в таблице представим следующим образом:

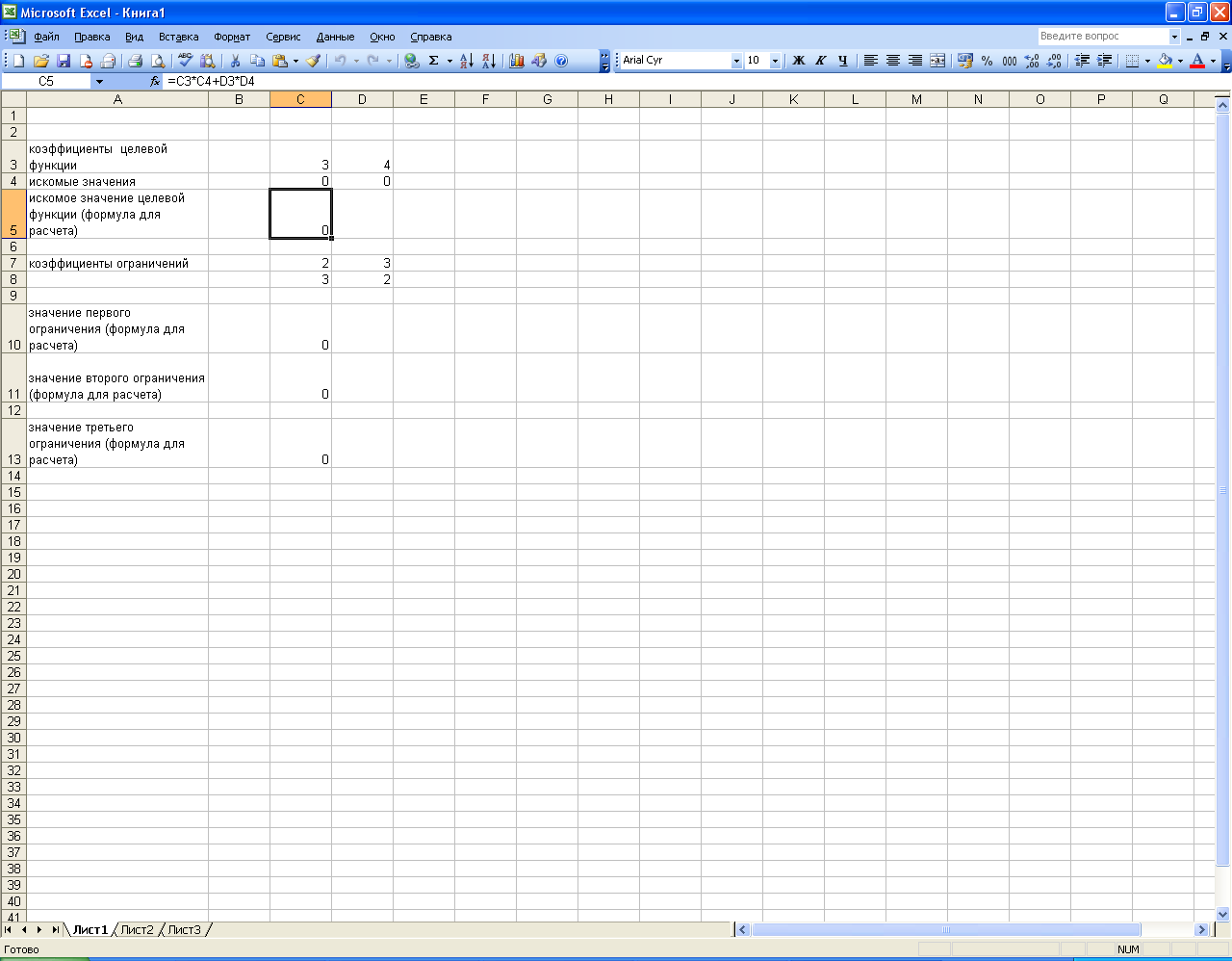
Выбираем в меню «Сервис» - «Поиск решения»

Далее «Установить целевую ячейку» : в данном случае значение целевой функции находится в ячейки С5

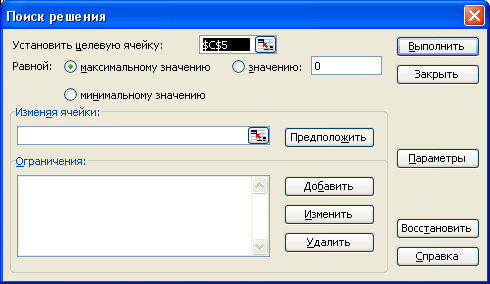
Вводим ячейки, в которых находятся искомые переменные

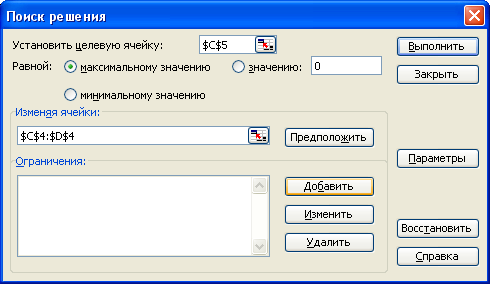
Далее нажимаем кнопку «Добавить» и вводим ограничения:

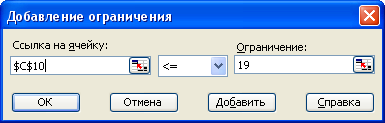
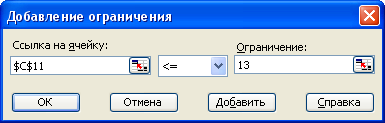
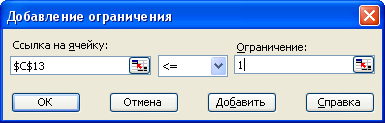
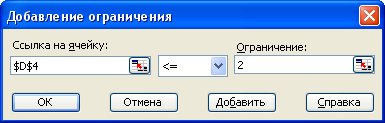
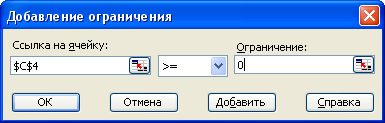
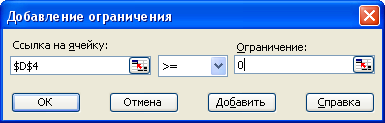
Полученный результат

3. Исходные данные.

Задание 1. Построить математическую модель задачи линейного программирования

Цех выпускает трансформаторы двух видов. Для изготовления трансформаторов обоих видов используются железо и проволока. Общий запас железа - 3 т, проволоки - 18 т. На один трансформатор первого вида расходуется 5 кг железа и 3 кг проволоки, а на один трансформатор второго вида расходуется 3 кг железа и 2 кг проволоки. За каждый реализованный трансформатор первого вида завод получает прибыль 3 д.е., второго - 4 д.е. Составьте план выпуска трансформаторов, обеспечивающий заводу максимальную прибыль.

Задание 2. Построить математическую модель задачи линейного программирования

Цех выпускает три вида деталей - А, В, С. Каждая деталь обрабатывается тремя станками.

Исходные данные приведены в таблице.

Отпускная цена детали А - 30 руб., детали В - 35 руб., детали С - 40 руб.

Составьте план загрузки станков, обеспечивающий получение максимального дохода.

Задание 3. Построить математическую модель задачи линейного программирования

Предприятие должно выпускать два вида продукции - А и В, используя при этом последовательно четыре станка. Данные о технологическом процессе представлены в таблице.

Станок	трудоемкость единицы продукции А, в мин.	трудоемкость единицы продукции В, в мин.	Фонд времени работы станков, в час.
1	3	3	15
2	2	6	18
3	4	0	16
4	1	2	8

Прибыль на единицу продукции А составляет 2$, продукции В - 3$.

Составьте план выпуска изделий, обеспечивающий наибольшую прибыль.

Задание 4. Построить математическую модель задачи линейного программирования

На предприятии для производства запасных частей для автомобилей используются три вида ресурсов. Выпускаются три вида запасных частей: А, В, С. Исходные данные приведены в таблице.

Прибыль от продажи одной запасной части А составляет 50 руб., для В - 80 руб., для С - 60 руб.

Составьте план производства запасных частей, обеспечивающих предприятию максимальную прибыль.

Задание 5. Построить математическую модель задачи линейного программирования

На заводе выпускают изделия четырех типов А, В, С, D. От реализации одного изделия завод получает прибыль соответственно 20, 10, 30, 50 руб. На изготовление изделий расходуются ресурсы трех типов: энергия, материалы, труд. Исходные данные приведены в таблице.

Спланируйте производство так, чтобы прибыль от реализации изделий была наибольшей.

24