
1)Математичні функції та процедури
Функція (математика)
Фу́нкція (відображення, трансформація, оператор) в математиці — це правило, яке кожному елементу з першої множини (області визначення) ставить у відповідність один і тільки один елемент з другої множини. Часто цю другу множину називають цільовою множиною чи образом функції чи відображення.
Відображення f, яке зіставляє кожному елементу множини A єдиний елемент множини B позначається як f:A→B (тобто f відображує A в B).
Інтуїтивне означення
Інтуїтивно, функція — це певне «правило», або «перетворення», яке зіставляє унікальне вихідне значення кожному вхідному значенню. Наприклад, в кожної особи є улюблений колір (жовто-блакитний, помаранчевий, біло-синій тощо). Улюблений колір є «функцією особи», тобто, наприклад, у Віктора улюбленим є помаранчевий, у Людмили — біло-синій. Тобто, вхідними значеннями тут є особи, вихідними — улюблені кольори. Або, наприклад, час, необхідний камінцю, кинутому з певної висоти, щоби досягнути землі, залежить від цієї висоти, яка тут виступає як вхідне значення, а час, який камінець знаходиться в польоті — в якості вихідного значення.
«Правило», яке визначає функцію, може бути задане формулою, певним співвідношенням або просто таблицею, в якій перелічені всі можливі комбінації вхідних та вихідних значень. Найважливішою ознакою звичайної функції є те, що вона завжди продукує однаковий результат на подане вхідне значення. Вхідне значення часто називають аргументом функції, вихідне — значенням функції
Зазвичай в функціях аргументами та значеннями виступають числа, і функціональна залежність задається формулою. Значення функції отримується безпосередньою підстановкою аргумента в формулу. Прикладом такої функції може бути квадратична залежність: f(x) = x2, яка зіставляє кожному аргументу його квадрат.
В загальнішому випадку, функція може бути залежною від декількох аргументів.
Втім, в сучасній математиці і природничих науках розглядаються функції, які не можуть бути явно задані формулами, тому сучасна інтерпретація поняття «функція» визначає її як певне відображення, відповідність між деякими множинами A (множиною або областю визначення) та B (яку іноді називають областю значень, хоча це й не зовсім правильно), отже таке відображення, яке зіставляє кожному елементу з множини A єдиний елемент з множини B. В теорії множин такі функції зручно визначати за допомогою відповідностей між множинами. В такій узагальненій інтерпретації функція стає фундаментальним поняттям практично в кожній галузі математичних знань.
Відсутність формального означення
Не існує формального означення функції. Поняття функція відноситься до базових понять математики, і його можна лише спробувати назвати іншим синонімом, наприклад відображення, відповідність, закон чи підмножина декартового добутку.
Функцією (відображенням, трансформацією) f множини X в множину Y (позначається f : X → Y) називається така відповідність між множинами X та Y, яка задовольняє наступним умовам:
Відповідність f всюди визначена, тобто, для будь-якого x з X існує такий y з Y, що x f y (y є образом x для функції f), тобто, для будь-якого x з X існує хоча б один образ y з Y.
Відповідність f є відповідністю багато-до-одного, або функціональною, тобто, якщо x f y та x f z, то y = z, тобто, y може бути образом зразу декількох елементів з X, але один елемент x не може породжувати більше одного образа з Y.
Елемент y з Y, який відповідає елементові x з X позначається як f(x).
Також можна сказати, що відображенням (функцією) з X в Y є така відповідність f⊆A×B, в якій кожному елементові a∈Pr1f відповідає тільки один елемент з Pr2f (тут × — Декартів добуток множин, Pr1f та Pr2f — відповідні проекції відображення).
Множина всіх функцій f : X → Y позначається як YX. При цьому потужність множини |YX| = |Y||X|.
Відповідність між X та Y, яка задовольняє тільки умові (1) називається багатозначною функцією. Будь-яка функція є багатозначною функцією, але не кожна багатозначна функція є функцією. Відповідність, яка задовольняє тільки умові (2) є часткова функція. Будь-яка функція є частковою, але не кожна часткова функція є функцією. В цій енциклопедії функцією є така відповідність між множинами, яка задовольняє одночасно умовам (1) та (2), якщо інше не вказується додатково.
Функції багатьох змінних, де y=f(x1, … , xn), тобто де y одночасно залежить від n змінних, можна визначити як відображення виду f: Xn → Y, де Xn — n-степень множини X (див. Декартів добуток множин).
Області значень та визначення
Докладніше: Область визначення та Область значень
X, множина вхідних значень, також називається областю визначення f, а Y, множина усіх можливих результатів, інколи називається областю значень, але більш коректно називати областю значень множину усіх тих елементів Y, для яких існують відповідні елементи з X. Тому в загальному випадку область значень є лише підмножиною Y.
Тотожною функцією (тотожним відображенням) називають функцію, область значень і визначення якої збігаються.
Ін'єктивні, сюр'єктивні та бієктивні функції
Існують спеціальні назви для деяких важливих різновидів функцій:
Ін'єктивна функція — функція, в якій різним значенням аргумента відповідають різні результати, тобто, для двох елементів x, y з Y виконується: f(x) = f(y) тоді й тільки тоді, якщо x = y.
Сюр'єктивна функція — функція f:X→Y, область значень якої збігається з множиною Y, тобто, для кожного y з Y існує x з X такий, що f(x) = y.
Бієктивна функція — функція, яка є одночасно сюр'єктивною та ін'єктивною, тобто встановлює взаємно однозначну відповідність між елементами множин X та Y.
Образ та прообраз
Образом елемента x∈X для відображення (функції) f є результат відображення (функції) f(x).
Образ підмножини A⊂X для f є така підмножина Y, яка відповідає умові:
f(A) = {f(x) | x ∈ A}
Слід зазначити, що область значень f збігається з образом області визначення f(X).
Прообраз відображення (або обернений образ) множини B ⊂ Y для f є підмножиною множини X, визначеною як
f −1(B) = {x ∈ X | f(x) ∈B}
Графік функції
Графік функції f є множина всіх впорядкованих пар (x, f(x)), для всіх x з області визначення X.
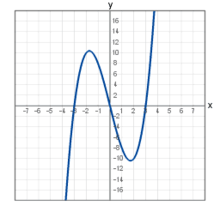
![]()
Графік кубічної функції. Ця функціє є сюр'єктивною, але не ін'єктивною
Композиція функцій
З функцій f: X → Y та g: Y → Z можна побудувати композицію функцій таким чином: спершу застосувавши f до аргумента x з X, а потім застосувавши g до результата. Така композиція функцій позначається g o f: X → Z, тобто (g o f)(x) = g(f(x)) для всіх x з X.
Тотожна функція, вкладення, продовження та звуження
Відображення (функція) E: X → X, таке, що E(x) = x для будь-якого x з X, має назву тотожного відображення, про яке говорять, що воно відображує X в себе.
Відображення I: X → Y, яке відображує елемент x з X в такий же елемент, але в Y, називається вкладенням
Відображення g': X → Y називається звуженням (обмеженням) відображення g: X' → Y' , якщо X та Y є підмножинами X' та Y' відповідно. Відображення g, в свою чергу, називається продовженням відображення g'.
Обернена функція
Деякі функції мають відповідні обернені функції. Нехай f: X → Y та g: Y → X деякі функції. Якщо композиція функцій f o g = EY, де E: Y→Y — тотожне відображення, то f має назву лівого оберненого до g, а g — правого оберненого до f. Якщо справедливо і f o g = EY і g o f = EX, то g має назву оберненого відображення (функції) до f і позначається як f−1.
Процедура (програмування)
|
Процедура (в програмуванні) — поняття, яке використовується в більшості мов програмування високого рівня, і відповідає значенню підпрограма.
Використання процедур
Використання кожної процедури пов'язане з її описанням та викликом. Описання процедури складається, як правило із заголовка процедури, та тіла процедури. Заголовок містить ідентифікатор процедури, та сукупність формальних параметрів, і, можливо, деякі їхні характеристики. Тіло процедури складається з деякої послідовності операторів. Виклик процедури відбувається із відповідних точок програми вказанням ідентифікатора процедури, її фактичних параметрів, і, можливо, входу в її тіло.
Типи процедур Процедури та функції
Розрізняють два способи використання процедур в програмах: в якості процедур-операторів, виклик яких представляє завершену одиницю дій мови програмування, та процедур-функцій, виклик яких здійснюється через відповідні вказівники функцій, які використовуються лише в якості складових елементів виразів мови програмування. Завжди, при виклику процедури, формальні параметри в тілі цієї процедури замінюються на фактичні (передача параметрів за посиланням), або їхніми значеннями (передача параметрів по значенню) і виконується перетворене таким чином тіло процедури.
Відкриті та замкнені процедури
Відповідно до способу зв'язування з основною програмою процедури ділять на відкриті та замкнені.
Відкриті процедури складаються з малої кількості команд, їх вставляють в тіло програми кожен раз, коли зустрічається їхній виклик.
Замкнені процедури розміщуються окремо від основної програми, при кожному виклику замкненої процедури, організовується відповідна передача управління та повертання в точку виклику. Як правило, стандартні процедури замкнені.
Особливий випадок представляє рекурсивна процедура та процедура без параметрів, виклик якої містить лише її ідентифікатор.
2)Сумісність типів
Мова Pascal є строго типізованою мовою програмування. У ній строго дотримується концепція типів даних, відповідно до якої всі операції, що застосовуються у мові, означені лише над операндами сумісних типів. Сумісність типів важливо враховувати у виразах та в операторі присвоєння значень змінним.
Можливість використання операндів різних типів у виразах називається сумісністю типів. Можливість присвоювати значення одного типу змінним іншого типу називається сумісністю за присвоєнням.
Два типи вважаються сумісними у виразах, якщо виконується хоча б одна з наступних умов:
типи двох операндів однакові;
типи двох операндів дійсні;
типи двох операндів цілочислові;
тип одного операнда є піддіапазоном типу іншого операнда;
типи двох операндів є піддіапазонами того самого базового типу;
тип одного операнда рядковий, тип іншого рядковий або символьний;
тип одного операнда — нетипізований покажчик, тип іншого операнда — будь-який типізований покажчик;
типи двох операндів процедурні — вони означують процедури (функції) з однаковою кількістю параметрів, однаковими типами відповідних параметрів і однаковими типами значень, що повертаються (для функцій).
Розглянемо декілька прикладів сумісності у виразах. В одному виразі можна використовувати дійсні та цілочислові операнди (1+2.5). Під час обчислення такого виразу спочатку цілочисловий операнд перетворюється на дійсний, а потім виконується зазначена операція над дійсними значеннями. Операнди можуть мати різні цілочислові типи. Якщо один операнд знаковий, а другий беззнаковий, обидва перетворюються до цілочислового знакового типу, якому можуть належати значення обох операндів і який вимагає найменшого обсягу оперативної пам'яті. Наприклад, операнди типів shortint і byte перетворюються на операнди типу integer, операнди типів shortint і word — на операнди типу longint. Якщо обидва операнди мають знакові цілочислові типи, або обидва мають беззнакові цілочислові типи, то операнд типу, що потребує меншого обсягу оперативної пам'яті, перетворюється на операнд типу, що вимагає більшого обсягу оперативної пам'яті (наприклад, операнд типу shortint перетворюється на операнд типу integer, операнд типу integer — на операнд типу longint, а операнд типу byte — на операнд типу word).
Під час виконання оператора присвоєння значення змінній обов'язково потрібно враховувати сумісність типів. Тип значення виразу є сумісним за присвоєнням із типом змінної, якій це значення надається, якщо виконується одна із таких умов:
тип змінної, яка набуває значення виразу, і тип виразу однакові;
тип змінної, яка набуває значення виразу, і тип виразу є сумісними порядковими типами, і діапазон значень типу виразу є піддіапазоном значень типу змінної;
тип змінної, яка набуває значення виразу, і тип виразу є дійсними типами, і діапазон значень типу виразу є піддіапазоном значень типу змінної;
тип виразу цілочисловий, а тип змінної, яка набуває значення виразу, дійсний;
тип виразу і тип змінної, яка набуває значення виразу, є рядковим;
тип виразу є символьним, а тип змінної, котра набуває значення виразу, є рядковим.
Отже, у програмі дані одного типу можуть перетворюватися на дані іншого типу. Таке перетворення типів може бути явним або неявним. Явне перетворення типів здійснюється за допомогою вбудованих функцій, аргументи яких мають один тип, а значення, що вони їх повертають, мають інший тип (функції ord, trunc, round, chr, ptr). Також явне перетворення типів можна здійснити шляхом запису перед узятим у круглі дужки виразом, тип якого перетворюється, ідентифікатора типу, на який тип виразу потрібно перетворити, наприклад: byte(false), integer( 'X'), char(60)). Якщо змінна zz має тип byte, кожне з присвоєнь char(zz) : = 'А' та zz:=byte( 'A') надасть цій змінній значення 65, а присвоєння shortint(zz) :=-100 - значення 156 (максимальне значення типу byte дорівнює 255, вводиться значення -100, результат після перетворення типу становитиме 255 + 1 - 100 = 156).
У прикладі 2.10 демонструється принцип використання операцій явного перетворення типів. На рис. 2.9 наведено результати роботи програми ех2_5.

Приклад 2.10
program ex2_5; var intvar:integer; symbolvar:char; begin writeln('Converting types'); writeln('Enter integer '); readln(intvar); writeln('byte(intvar)=',byte(intvar)); writeln('Enter character '); readln(symbolvar); writeln('integer(symbolvar)=',integer(symbolvar)); writeln('char(intvar+5)=',char(intvar+5)); writeln('byte(false)=',byte(false)); readln; end.
Рис. 2.9. Результати роботи програми ех2_5. Перетворення типів
Демонстрація прикладу
Неявне перетворення типів здійснюється при використанні в одному виразі або в одному операторі присвоєння сумісних, але різних типів даних.
Дійсні типи сумісні між собою за присвоєнням. Але якщо деяке дійсне значення виходить за межі діапазону допустимих значень певного дійсного типу, назвемо його R, то перетворення типу цього значення на R під час виконання програми призведе до помилки.
Натомість, якщо деяке ціле значення виходить за межі діапазону допустимих значень певного цілочислового типу, назвемо його Т, то перетворення типу цього значення на Гдо помилки не призведе, але частина бітів у двійковому записі даного значення буде відкинута. Наприклад, значення виразу byte (260) дорівнює 4, оскільки 4 — це значення молодшого байта двохбайтового числа 260.
