4.3. Базис векторного простору, розклад вектора за базисом

Лінійно незалежна підсистема набору векторів називається максимальною лінійно незалежною підсистемою, якщо дописування до неї довільного вектору цього набору, який не входить в цю підсистему, робить її лінійно залежною.

Твердження. Максимальні лінійно незалежні підсистеми даного набору векторів можна вибирати по-різному, але кількість векторів кожної з них – однакова.

Кількість векторів у максимальній лінійно незалежній підсистемі даного набору векторів називається рангом набору.

Максимальна лінійно незалежна підсистема векторів простору називається базисом цього простору, а кількість векторів в цій підсистемі співпадає з розмірністю простору.

Висновок. Очевидно, базис є мінімальним набором векторів простору, якого досить, щоб всі інші вектори простору можна було подати у вигляді лінійних комбінацій векторів цього набору.

Теорема (про розклад вектора простору за базисом). Якщо – деякий базис векторного простору , тоді будь-який вектор однозначно подається у вигляді лінійної комбінації базисних векторів, тобто існує єдиний набір дійсних чисел такий, що , при цьому набір називається координатами вектора у базисі , а дана лінійна комбінація називається розкладом за базисом.

Теорема. Якщо – лінійно незалежний набір векторів простору, причому будь-який вектор цього простору лінійно виражається через вектори набору , то:

1) – базис даного простору;

2) простір – n-вимірний.

На практиці для знаходження розкладу вектора за базисом використовують наступну схему, яку ми проілюструємо на прикладі.

Приклад 4. Перевірити, що набір векторів 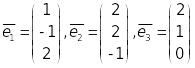є базисом та розкласти вектор 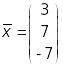за цим базисом.

Прирівняємо вектор до лінійної комбінації векторів набору , де числа поки що невідомі. Запишемо цю рівність у координатах векторів:

.

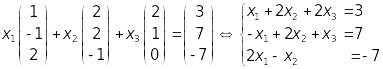Отже, отримали неоднорідну СЛР, розв’язуючи яку знайдемо коефіцієнти розкладу вектора за набором векторів . Для цього скористаємось методом Жордана-Гауса:

.

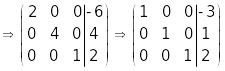Очевидно, СЛР – сумісна та визначена, отже, вектори набору утворюють базис, оскільки набір є лінійно незалежним, кількість векторів співпадає з їх розмірністю. Координати вектора в цьому базисі (–3, 1, 2).

Таким чином, набір векторів є базисом простору, розклад вектора за цим базисом має вигляд .

Зауваження. Приклад показує, що для знаходження розкладу вектора за набором векторів слід скласти матрицю, стовпчиками якої є вектори набору, а стовпчиком вільних членів – вектор . Вважаючи цю матрицю розширеною матрицею неоднорідної СЛР, слід розв’язати систему методом Гауса або Жордана-Гауса. При цьому можливі випадки:

1) якщо СЛР виявиться несумісною, то вектор не розкладається за векторами набору, отже набір векторів не є базисом;

2) якщо СЛР виявиться сумісною, але невизначеною, то вектор розкладається за векторами цього набору, але неоднозначно, отже набір векторів не є базисом, оскільки вектори набору лінійно залежні;

3) якщо СЛР виявиться сумісною та визначеною, то вектор розкладається за векторами цього набору однозначно, отже вектори набору лінійно незалежні, причому за умови, що їх розмірність співпадає з кількістю (кількість рівнянь системи співпадає з кількістю невідомих), набір векторів є базисом простору.