Раздел іi Статистика ринку

Задача 6. Статистичне дослідження ринкового попиту.

Дані про обсяги продажів однотипної продукції машинобудівного заводу на двох субринках за вільними цінами наведено в таблиці 6 по варіантах. Необхідно зробити висновок про рівність або розходження умов продажів машинобудівної продукції на субринках, а також про рівень розходження цін на продажну продукцію.

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Дані про обсяги продажів однотипної продукції

№ ринку	Кількість проданої продукції, шт.	Середня ціна продажу, грн.	Дисперсія цін
1	12	31,2	8,4
2	18	29,2	4,0

Т.к. дисперсії відрізняються, то попередньо перевіряємо нульову гіпотезу про рівність генеральних дисперсій:

при конкуруючій гіпотезі

Використовуємо критерій Фішера-Снедекора, як відношення більшої дисперсії до меншої.

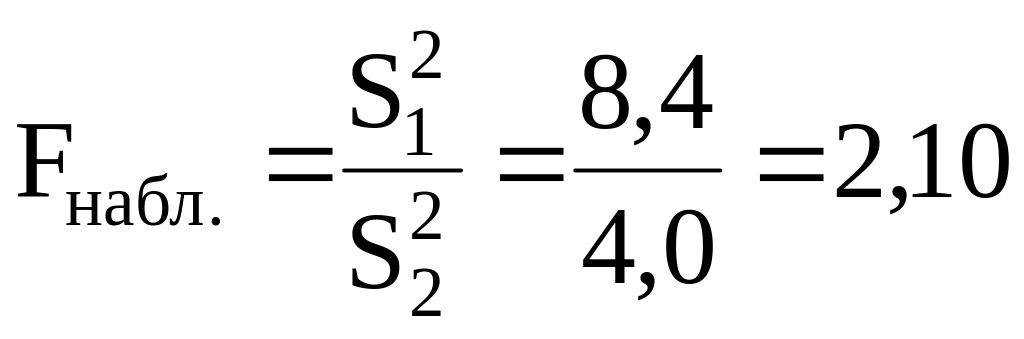
По таблиці граничних значень F-критерія Фішера-Снедекора: при числі ступенів свободи k₁=n₁–1=12–1=11, k₂=n₂–1=18–1=17 і при рівні значимості α = 0,05 знаходимо границі двосторонньої критичної області критерію (додаток А).

Т.к. F_набл<F_кр (2,10<2,41), то нема підстави відкидати нульову гіпотезу про рівність генеральних дисперсій. Отже, умови продажу продукції на двох товарних ринках рівні.

Перевіряємо нульову гіпотезу про рівність двох середніх нормальних генеральних сукупностей, дисперсії яких рівні:

при конкуруючій гіпотезі

Для цього обчислимо значення критерію Ст`юдента.

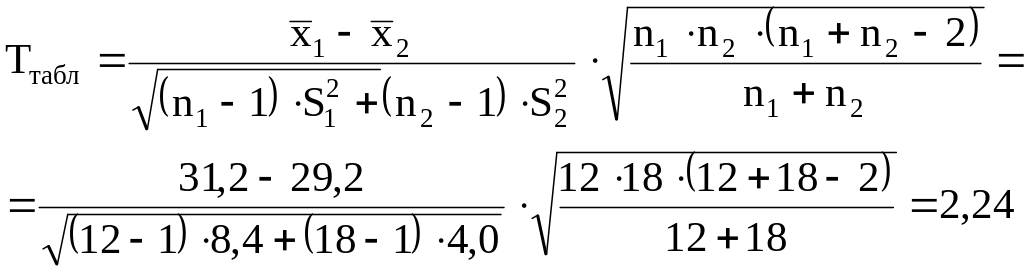
По таблиці граничних значень двостороннього t-розподілу Ст`юдента знаходимо при числі ступенів свободи k₁=n₁+ n₂–2=12+18–2=28 і прийнятому рівні значимості =0,05 (додаток Б):

Т.к. Т_набл>t_кр (2,24>2,05), то нульову гіпотезу про рівність середніх генеральних сукупностей відкидаємо, тобто середні ціни продажів на двох товарних ринках розрізняються значно.

Задача 7. Статистичне дослідження ринкового попиту.

Підприємство, що виробляє товар масового попиту, планує підвищити ціни на цей товар. У ряді торговельних місць був проведений експеримент, у результаті якого отримані дані, що характеризують еластичність обсягів продажів товару щодо темпів підвищення цін (табл. 7). Необхідно побудувати графік залежності обсягів продажів, від темпів підвищення цін, виділить на графіку зони стійких і хитливих обсягів продажів, обчислить коефіцієнти еластичності для цих зон, зробити висновок про припустиму межу підвищення ціни, що не робить істотного впливу на зміну обсягів продажів даного товару.

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Умовне позначення		Значення змінних
x, %		100,5		101		101,5		102		102,5		103		103,5		104		104,5		105
У, тис. шт.	120		124		120		122		120		120		116		112		116		110
	116		120		118		120		116		118		112		110		112		106

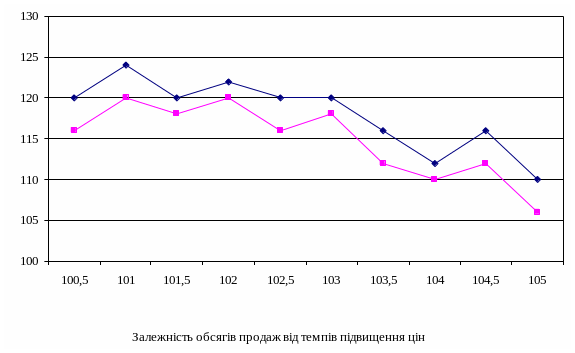
Графік залежності обсягів продажу від темпів підвищення цін наведено на рисунку.

Відносно стійкі обсяги продажів автомобільного бензину спостерігаються в зоні підвищення ціни від 101% до 104%. При підвищенні ціни понад 104% спостерігається істотне скорочення обсягів продажів. Обчислимо коефіцієнти еластичності обсягів продажів щодо темпів підвищення ціни для зон стійких і хитливих обсягів продажів. Коефіцієнт еластичності:

,

де а1	– коефіцієнт регресії кореляційного рівняння зв'язку
x	– значення, що спостерігається, або середнє значення перемінної x
y	– значення, що спостерігається, або середнє значення перемінної y

Складається розрахункова таблиця.

Зона стійких обсягів продажу

х	у	х2	ху	К ух
100,5	120	10100,25	12060	-0,23929
100,5	116	10100,25	11658	-0,24754
101	124	10201	12524	-0,23272
101	120	10201	12120	-0,24048
101,5	120	10302,25	12180	-0,24167
101,5	118	10302,25	11977	-0,24576
102	122	10404	12444	-0,23888
102	120	10404	12240	-0,24286
102,5	120	10506,25	12300	-0,24405
102,5	116	10506,25	11890	-0,25246
103	120	10609	12360	-0,24524
103	118	10609	12154	-0,24939
1221	1434	124245,5	145907	–

Зона хитливих обсягів продаж:

х	у	х2	ху	К ух
103,5	116	10712,25	12006	-2,67672
103,5	112	10712,25	11592	-2,77232
104	112	10816	11648	-2,78571
104	110	10816	11440	-2,83636
104,5	116	10920,25	12122	-2,70259
104,5	112	10920,25	11704	-2,79911
105	110	11025	11550	-2,86364
105	106	11025	11130	-2,9717
894	86947	93192	894	–

Обчислимо показники для зони стійких обсягів продажів. Коефіцієнт регресії:

Середній коефіцієнт значимості для цієї зони:

Отримане значення середнього коефіцієнта еластичності показує, що в розглянутій зоні при підвищенні ціни на автомобільний бензин на 1% обсяг продажів скорочується в середньому на 0,243 тис. ед.

Поточне значення коефіцієнтів еластичності для величин, що спостерігаються, x і y обчислюється в наступному порядку. Для першої пари спостережень:

Для наступних пар спостережень обчислення здійснюються аналогічно. Результати обчислень приведено в розрахунковій таблиці.

Обчислимо показники для зони хитливих обсягів продажів. Коефіцієнт регресії:

Середній коефіцієнт значимості для цієї зони:

Отримане значення середнього коефіцієнта еластичності показує, що в даній зоні при підвищенні ціни на автомобільний бензин на 1% обсяг продажів скорочується в середньому на 2,798 тис. од., тобто скорочення обсягу продажів є істотним.

Результати обчислень поточних коефіцієнтів еластичності приведені в розрахунковій таблиці.

Економічно обґрунтований висновок за даними статистичного аналізу полягає в тому, що ціна на бензин може бути підвищена на 3% без істотного скорочення обсягів продажів. При більш високому підвищенні цін обсяги продажів можуть різко знизитися.

Задача 8. Статистика продаж

Відвідувач, що ввійшов у магазин, за своїм розсудом може купити або не купити запропонований товар. При наявності реклами товару з боку продавця і ввічливого обслуговування імовірність покупки товару підвищується (табл. 8). Скільки відвідувачів необхідно обслужити, щоб з імовірністю p_n=0,95 можна було очікувати, що буде здійснено не менш визначеного числа покупок? На скількох може скоротитися кількість відвідувачів, що не купили товар, при проведенні реклами товару з боку продавця і ввічливого обслуговування?

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Відповідно до інтегральної теорії Лапласа

,

где pn(k1; n)	– імовірність появи очікуваного результату
k1	– необхідна кількість покупок
k2=n	– кількість клієнтів, що обслуговуються
р	– імовірність покупки товару
q=1-p	– протилежна імовірність, коли клієнт не купує товар

p_n(k₁; n)=0,95

k₁=75

р₁=0,5; p₂=0,8

q₁=0,5; q₂=0,2.

1) Визначимо необхідну кількість клієнтів магазина для забезпечення 75 покупок при відсутності реклами:

Оскільки чи , тоді .

Звідси

По таблиці значень інтегральної функції Лапласа (додаток В) знаходимо:

, тоді

Рішення квадратного рівняння відносно дає наступний результат:

, т.к. х>0, то

відвідувач.

2. Визначимо необхідну кількість клієнтів магазина для забезпечення 75 покупок при наявності реклами і ввічливого обслуговування.

Так як чи , тоді .

Звідси

По таблиці значень інтегральної функції Лапласа (додаток В) знаходимо:

, тоді

Рішення квадратного рівняння відносно дає наступний результат:

, т.к. х>0, то

відвідувачів.

Скорочення кількості клієнтів при проведенні реклами товару з боку продавця для забезпечення 75 покупок складає

чоловіка.

Задача 9. Статистична оцінка конкурсу товарів

Два незалежних експерти зробили оцінку товарів, наданих фірмою на конкурс, і розташували їх по наступних місцях (табл. 9). Необхідно встановити міру тісноти зв'язку між оцінками експертів, оцінити погодженість дій експертів і зробити висновок за результатами експертизи.

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Фірми	№	А	Б	В	Г	Д	Е	Ж	З
Експерт 1	1	1-2	1-2	3	4	5	6-7-8	6-7-8	6-7-8
Експерт 2	2	1	2	3	4-5-6	4-5-6	4-5-6	7	8

У даному випадку має місце рангова кореляція. Тому що кількість рівнів оцінки m=2 мають місце зв'язані пари оцінок, то можна застосувати коефіцієнт кореляції рангів для пов'язаних пар оцінок у послідовностях.

,

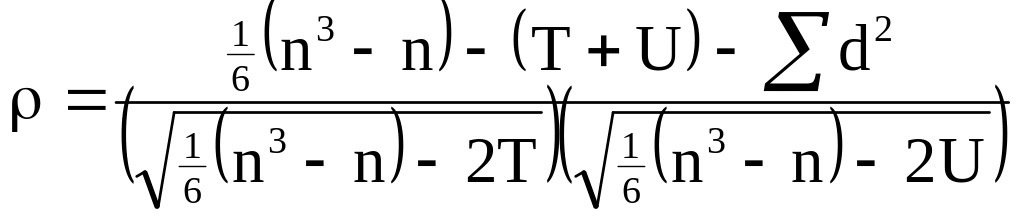де d	– величина різниці між рангами d=x-y
n	– кількість рангів у досліджуваній сукупності
T и U	– сумарні параметри пов'язаних пар у послідовності

;

де t, u

– число зв'язаних пар у послідовності

Аналіз таблиць вихідних даних показує, що експерт 1 поділив перше і друге місця між фірмами А и Б, їх ранг 1,5. Фірма В - на 3 місці, фірма Г - 4 місце, фірма Д - 5 місце. Фірми Е, Ж, З поділили 6, 7 і 8 місця. Їх об'єднаний ранг (6+7+8)/3=7.

Експерт 2 поставив фірму А на 1 місце, фірму Б - на 2 місце, фірма В - 3 місце. Фірми Г, Д, Е поділили 4, 5 і 6 місця. Їх об'єднаний ранг (4+5+6)/3=5. Фірма Ж зайняла 7 місце, а фірма З - 8 місце.

Для цього випадку:

Для обчислення складемо таблицю відхилень між об'єднаними рангами:

Фірми	А	Б	В	Г	Д	Е	Ж	З
Експерт 1	1,5	1,5	3	4	5	7	7	7
Експерт 2	1	2	3	5	5	5	7	8
d	-0,5	0,5	0	-1	0	2	0	1
d2	0,25	0,25	0	1	0	4	0	1

Для тісноти зв'язку обчислимо коефіцієнт рангової кореляції:

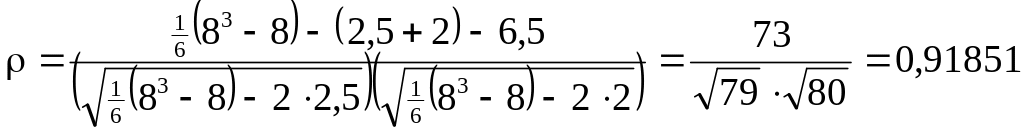
Величина кореляції рангів , отже, тіснота зв'язку між оцінками експертів досить висока, дії експертів найвищою мірою погодяться між собою, результати експертизи можуть бути прийняті.

Задача 10. Статистична оцінка конкурсу товарів

На конкурс представлені шість моделей одягу, що оцінюються незалежними експертами. Моделі по оцінці одержали наступні місця, що представлені в табл. 10. Необхідно установити, наскільки погоджено діяли експерти, і зробити висновок за результатами експертизи.

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Модель	А	Б	В	Г	Д	Е	Ж
Експерт 1	4	7	1	5	2	6	3
Експерт 2	3	7	4	6	1	5	2
Експерт 3	4	6	2	7	3	5	1
Експерт 4	3	4	3	6	2	7	5
Експерт 5	7	5	1	2	3	6	4
Сума місць	21	29	11	26	11	29	15
Розподіл місць	4	6-7	1-2	5	1-2	6-7	3

По мінімальній сумі місць кращими визнані моделі В і Д.

У даному випадку має місце рангова кореляція. Тому що кількість рівнів оцінки m>2, то для оцінки дій експертів застосовується коефіцієнт конкордації:

де d	– величина різниці між сумою рангів і середнім значенням суми рангів одного об'єкта
m	– число послідовностей
n	– кількість моделей

Для визначення d обчислюємо середнє значення суми рангів одного об'єкта як середню суму рангів:

Даний результат можна одержати також з вираження:

Параметр d обчислюють як різниця між сумою рангів, виставлених експертами для одного об'єкта, і середньою сумою рангів. Результат розрахунків приводиться в таблиці.

Модель	А	Б	В	Г	Д	Е	Ж
Сума місць	21	29	11	26	11	29	15
Середня сума місць	20	20	20	20	20	20	20
d	1	9	1	6	1	9	5
d2	1	81	1	36	1	81	25

Для оцінки кореляції рангів обчислюємо коефіцієнт конкордації:

Величина коефіцієнтів, що спостерігається, кореляції рангів W=0,3228<0,7, отже, дії експертів погодяться погано, результати експертизи не можуть бути прийняті.

Задача 11. Статистична оцінка умов постачання і вхідного контролю.

Для забезпечення підприємства дефіцитними матеріалами агенти з постачання направляються до постачальників. Імовірність успішного забезпечення постачання в результаті одного відвідування наведено в табл. 11. Необхідно знайти імовірність постачання матеріалу хоча б одним з постачальників. Скільки необхідно направити агентів з постачання за умови, що кожний з них може відвідати не більш двох різних постачальників.

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Імовірність настання події А в n незалежних іспитах:

,

де p	– імовірність забезпечення постачання
q	– імовірність протилежної події
n	– кількість незалежних іспитів

р₁=0,6.

Т.к. для одного агента постачання n₁2, то для m агентів – n₁2m. Визначимо ситуацію, при якій буде дотримана умова даного приклада р(А)0,97.

При , тобто при одному агенті постачання умова не виконується.

При , тобто при двох агентах постачання умова виконується.

Таким чином, з імовірністю два агенти постачання забезпечать постачання матеріалу хоча б одним постачальником.

Задача 12. Статистична оцінка умов постачання і вхідного контролю.

Надійшло декілька партій сировини для текстильного підприємства. На кожній партії відібрано по декілька зразків пряжі і проведені іспити на визначення величини розривного навантаження. Результати іспитів приведені в таблиці 12. Визначити, чи істотно впливають різні партії сировини на величину розривного навантаження?

	Міцність матеріалу, од.
	1 зразок	2 зразок	3 зразок	4 зразок
1	400	380	460	300
2	280	300	380	340
3	340	420	400	300
4	270	300	380	340
5	330	300	400	300

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Рішення виконуємо за допомогою методу однофакторного дисперсійного аналізу. Перевіряємо нульову гіпотезу про однорідність сировини, що надійшло.

Обчислимо середні арифметичні величини для кожної партії пряжі:

Обчислимо загальну середню величину для всієї сукупності партій і зразків:

Обчислимо суму квадратів відхилень між групами (партіями):

з кількістю ступенів свободи k₁=m-1=5-1=4.

Обчислимо суму квадратів відхилень усередині груп:

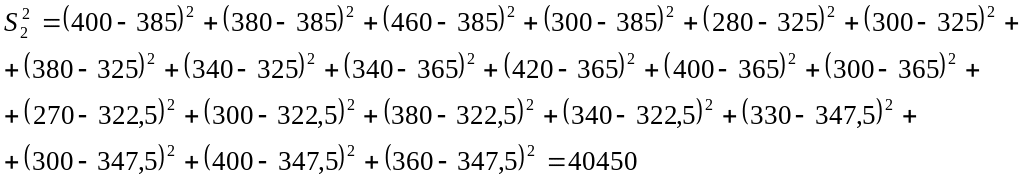
з кількістю ступенів свободи k₂=mn-m=54-5=15.

Обчислимо повну суму квадратів відхилень від загальної середньої величини:

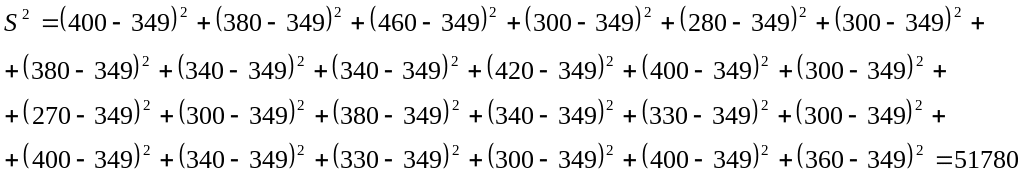
з кількістю ступенів свободи k=mn-1=54-1=19.

Результати обчислень зведемо в таблицю однофакторного дисперсійного аналізу.

Компоненти дисперсії	Суми квадратів	Число ступенів свободи	Середній квадрат
Поміжгрупова,	2832,5	4	708,125
Внутригрупова,	40450	15	2696,67
Повна,	51780	19	2725,26

Обчислимо значення, що спостерігається, F-критерію розподілу Фішера-Снедекора як відношення більшого середнього квадрата до меншого:

По таблиці критичних значень F-розподілу Фішера-Снедекора знаходимо табличне значення при числі ступенів свободи k₁=4 і k₂=15 і рівні значимості =0,05:

Так как F_набл.>F_табл. (3,808>3,09), то нульову гіпотезу відкидаємо, тобто розходження між сировиною в партіях впливає на величину розривного навантаження нитки, і сировина не можна прийняти однорідним.

Задача 13. Статистичне вивчення втрат товару в путі й обґрунтування страхових платежів

Підприємство відправило замовникові партію виробів. Вироби можуть бути загублені або зіпсовані в путі з визначеною імовірністю. Вихідні дані для рішення задачі приведені в табл. 13. Необхідно визначити, скільки виробів може бути загублені в путі і з якою імовірністю? На яку суму варто застрахувати дану партію виробів для відшкодування можливих втрат у путі? Норму страхової компанії прийняти 28%.

РІШЕННЯ ТИПОВОЇ ЗАДАЧІ

Підприємство відправило замовникові партію з 500 виробів. Імовірність втрати виробів у путі складає 0,2%. Скільки виробів може бути загублене в путі і з якою імовірністю? На яку суму варто застрахувати дану партію виробів для відшкодування можливих втрат у путі? Норму страхової компанії прийняти 36%.

Імовірність настання рідкої події визначається за законом розподілу імовірностей дискретної випадкової величини - законові Пуассона:

,

де k	– число появ незалежних подій
	– середнє число або середня інтенсивність появи події в n іспитах
p	– імовірність появи події

n=500

Середня інтенсивність втрат на одну партію виробів:

шт.

Імовірність відсутності втрат виробів у путі:

Імовірність втрати одного виробу у путі:

Імовірність втрати двох виробів у путі:

Імовірність втрати трьох виробів у путі:

Імовірність втрати чотирьох виробів у путі:

Імовірність втрати п`яти виробів у путі:

Імовірність втрати шості виробів у путі:

Імовірність втрати сьомі виробів у путі:

Імовірність втрати восьмі виробів у путі:

Через досить малу імовірність втрати більш чотирнадцяти виробів, подальші обчислення припиняємо.

Складемо робочу таблицю, у яку внесемо обчислені імовірності, середнє число виробів, що втрачаються, шляхом перемножування імовірності втрати на число виробів, що втрачаються, по рядках і накопичене число виробів, що втрачаються, шляхом порядкового підсумовування:

Число виробів, що втрачаються	Імовірність утрати даної кількості, pn(k)	Середнє число виробів, що втрачаються, kpn(k)	Накопичене число виробів, що втрачаються, kpn(k)
0	0,36788	0	0
1	0,36788	0,36788	0,36788
2	0,18394	0,36788	0,73576
3	0,06131	0,18393	0,91969
4	0,01533	0,06132	0,98101
5	0,00307	0,01535	0,99636
6	0,000511	0,00307	0,99943
7	0,000073	0,00051	0,99994
8	0,000008	0,00006	1,00000

Накопичене число виробів, що втрачаються, у процесі дорівнює середньої інтенсивності втрат:

kp_n(k)==1,0

Норма доходу страхової компанії а=36% установлюється стосовно вартості середнього числа втрат даного товару в путі. Тому страхова сума складе не менш S.

од. вартості виробу.