
- •Розділ і Невизначений інтеграл
- •§1. Первісна для функції
- •§2. Невизначений інтеграл
- •§3. Основні прийоми інтегрування
- •Результатом застосування формули (3.1) двічі є
- •Аналогічно допускають повне обчислення і інтеграли виду
- •Навпаки, не можуть бути представлені через елементарні функції інтеграли
- •§4 Техніка невизначеного інтегрування
- •Розглянемо спочатку інтегрування простих раціональних функцій. Такими є:
- •Таким чином,
- •Розглянемо окремо інтеграл
- •Поділимо на нього чисельник, після чого одержимо
- •Так, функції
- •2. Деякі інтеграли, які раціоналізуються
- •Тому інтеграл
- •3. Інтеграли від деяких ірраціональних виразів Розглянемо інтеграл виду
- •Але інтеграли виду
- •Інтеграл
- •Але можна діяти і інакше, якщо зробити підстановку
- •§5. Інтеграл від диференціального бінома
- •§ 6. Мішані типові задачі на інтегрування
Поділимо на нього чисельник, після чого одержимо
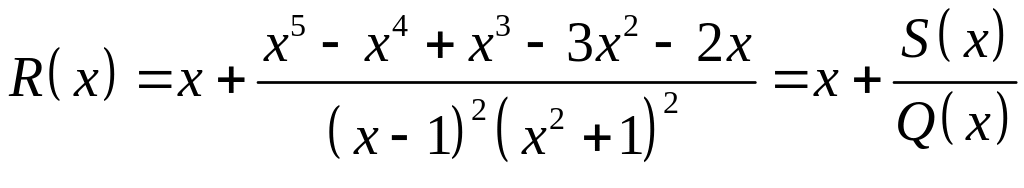 .
.
Розкладемо правильний дріб на суму простіших
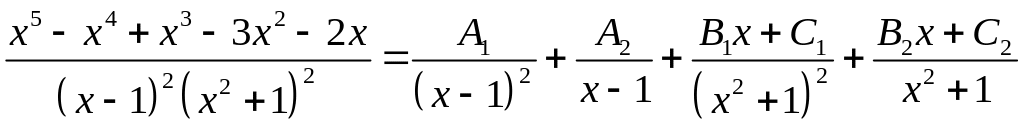 ,
,
де
![]() .
.
Для
визначення
![]() перенесемо
перенесемо
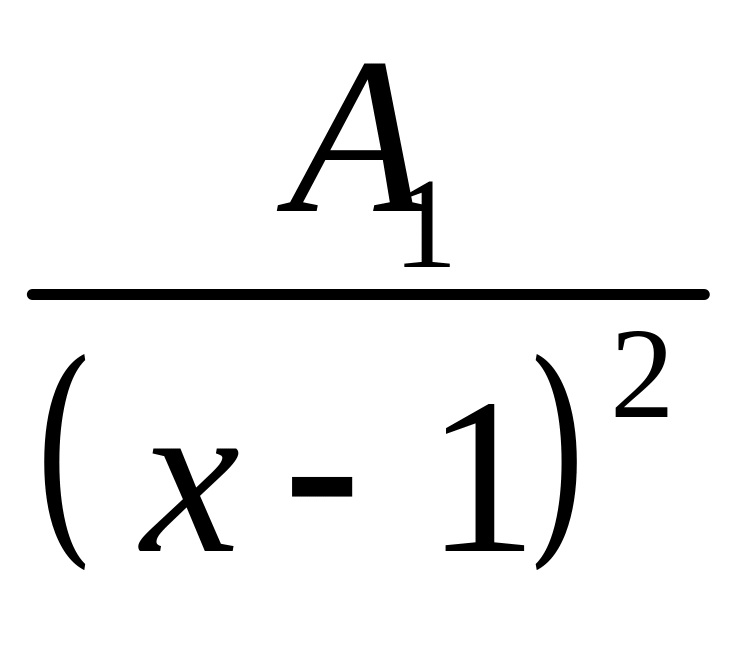 в ліву частину і одержимо
в ліву частину і одержимо
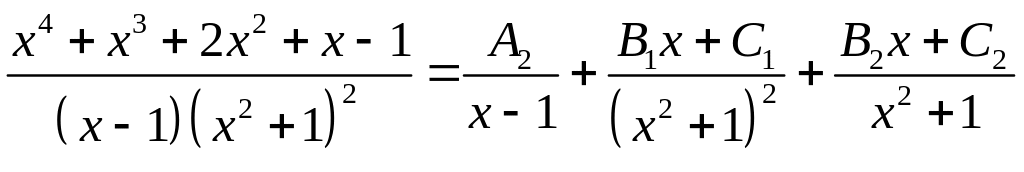 ,
,
звідки
![]() .
.
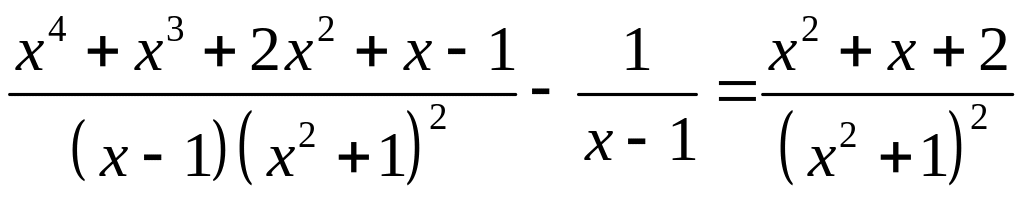 ,
,
А тоді, аналогічно
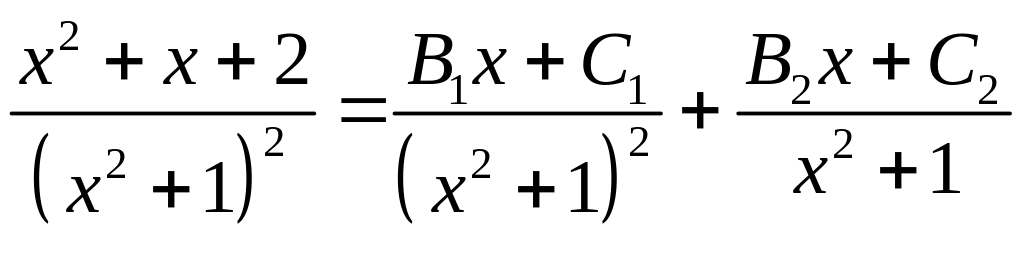
Після приведення до загального знаменника виразу в правій частині, та прирівнюючи коефіцієнти при однакових степенях , отримаємо
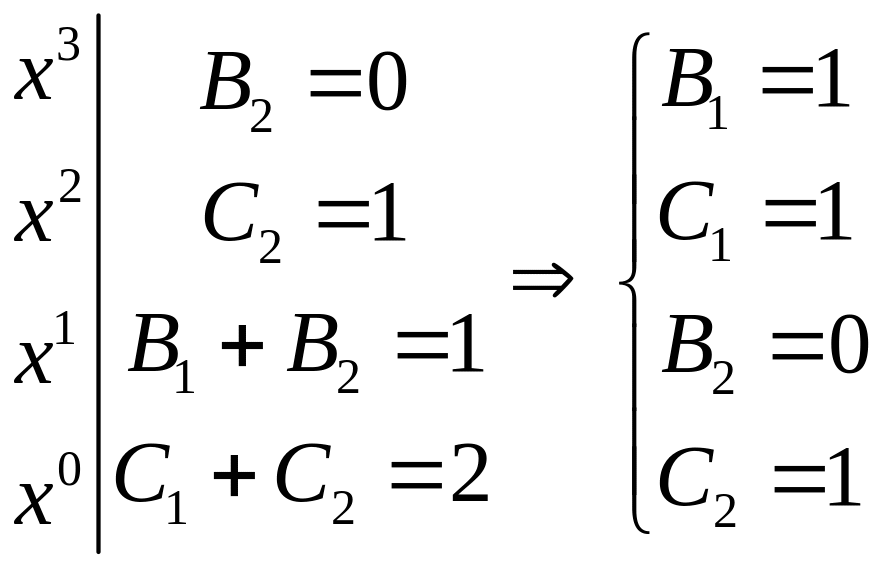
Таким чином,
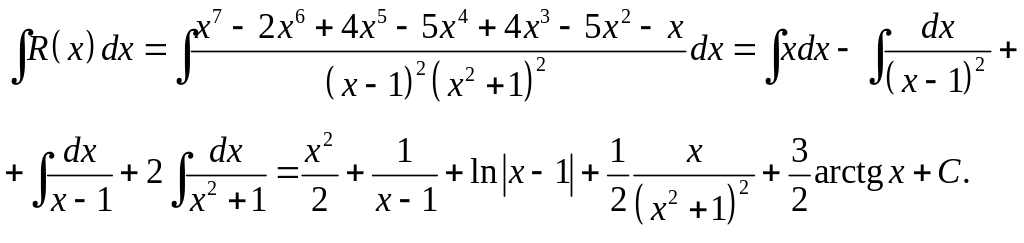
Відмітимо,
що первісна для будь-якої раціональної
функції
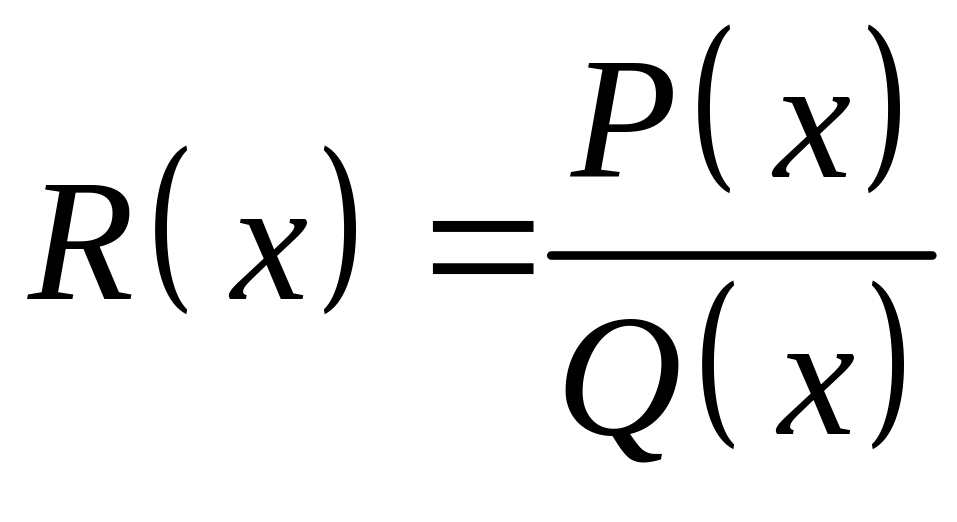 виражається через раціональні функції,
а також трансцендентні функції
виражається через раціональні функції,
а також трансцендентні функції
![]() та
та
![]() ,
причому трансцендентні функції
появляються, коли є прості дроби
,
причому трансцендентні функції
появляються, коли є прості дроби
![]() та
та
![]() типу.
типу.
Зауваження. Якщо результатом заміни в невизначеному інтегралі підінтегральна функція вже є раціональною, то кажуть, що „інтеграл раціоналізується”. Розглянемо деякі класи функцій, які можна раціоналізувати.
Функцію
![]() називають раціональною відносно
називають раціональною відносно
![]() ,
якщо над змінними
проводяться дії
,
якщо над змінними
проводяться дії
![]() скінчену кількість разів.
скінчену кількість разів.
Так, функції
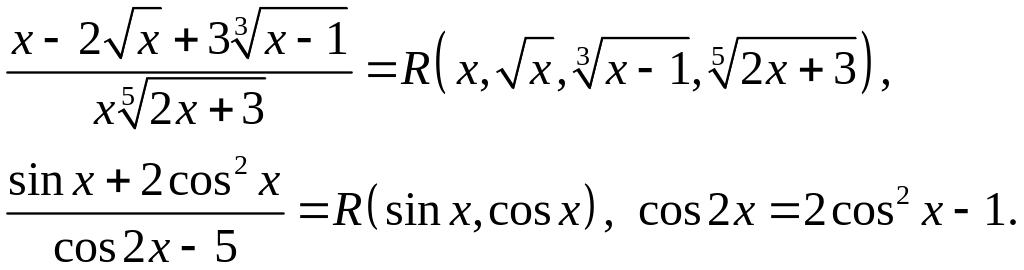
2. Деякі інтеграли, які раціоналізуються
За допомогою
стандартних підстановок деякі типи
інтегралів можна звести до інтегралів
від раціональних функцій. У подальшому
нагадаємо, що
![]() означає
раціональну функцію від одного або
кількох аргументів.
означає
раціональну функцію від одного або
кількох аргументів.
а) Інтеграл виду
![]()
раціоналізується
заміною
![]()
Приклад 4.6.
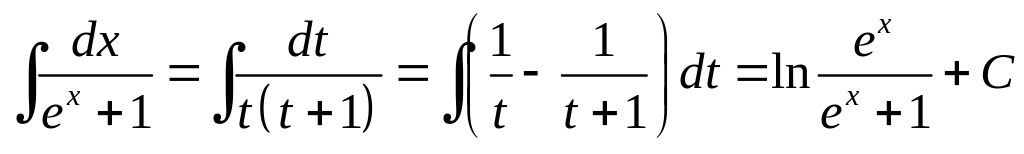
б) Інтеграл виду
![]()
раціоналізується
підстановкою
![]() .
Раціональними від
.
Раціональними від
![]() зокрема будуть
зокрема будуть
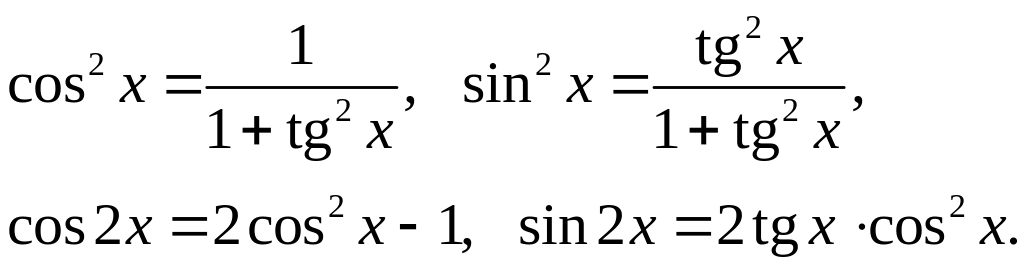
Тому інтеграл
![]()
також
раціоналізується підстановкою
![]() .
.
Приклад 4.7.
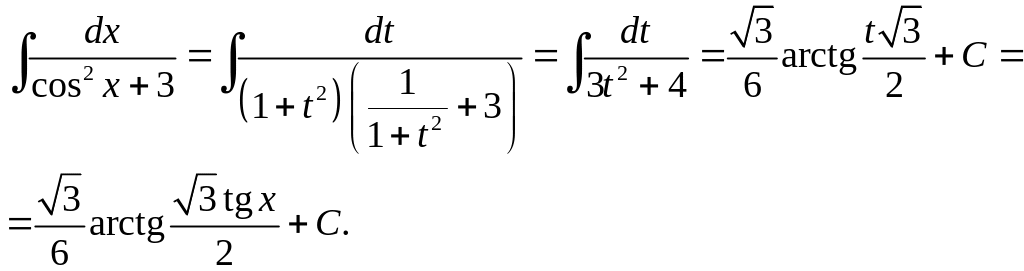
Але функції
![]() не будуть раціональними функціями від
(вже, наприклад, тому, що
має період
не будуть раціональними функціями від
(вже, наприклад, тому, що
має період
![]() ,
а
та
,
а
та
![]() ). Але вони будуть раціональними функціями
від
). Але вони будуть раціональними функціями
від
![]() :
:
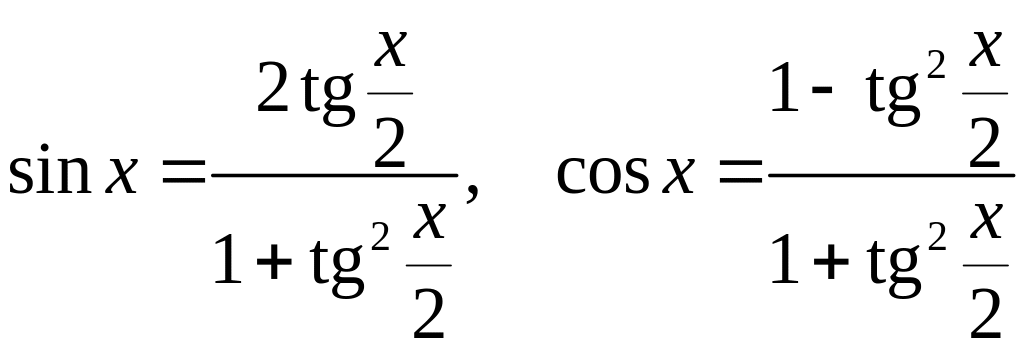
і при
цьому
![]() ,
а тому інтеграл виду
,
а тому інтеграл виду
![]()
раціоналізується
підстановкою
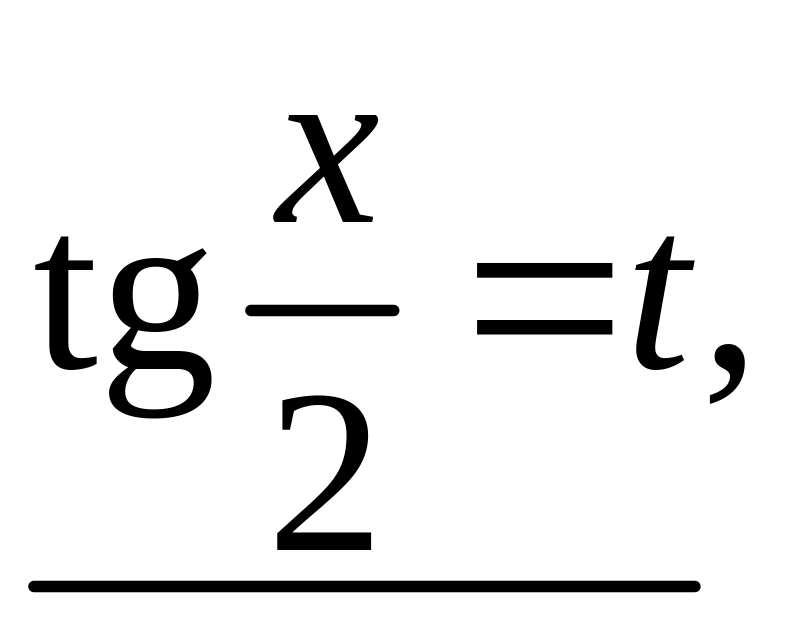 яку часто називають “універсальною
тригонометричною підстановкою”.
яку часто називають “універсальною
тригонометричною підстановкою”.
Приклад 4.8.
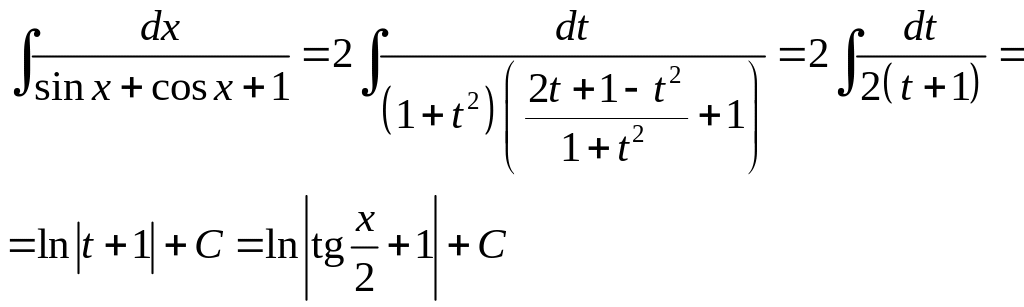
Якщо
функція
![]() така,
що
така,
що
![]() ,
,
то більш
ефективною в деяких випадках є підстановка
![]() .
.
Приклад 4.9.
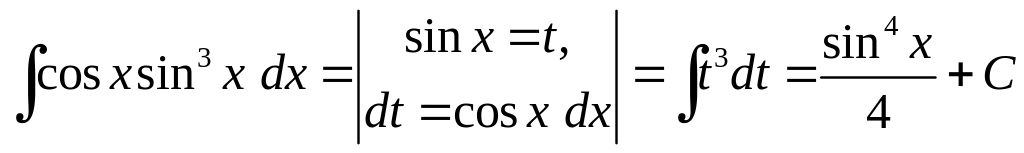 .
.
Можлива
в цьому випадку і підстановка
![]() ,
тоді
,
тоді
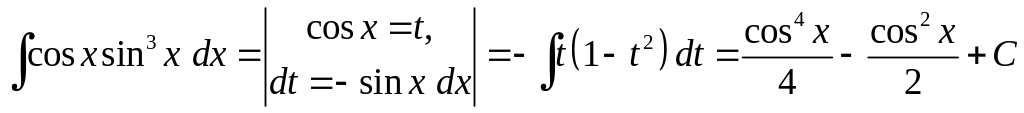 .
.
Неважко
перевірити, що первісні для
![]() та
та
![]() відрізняються на сталу. Дійсно
відрізняються на сталу. Дійсно
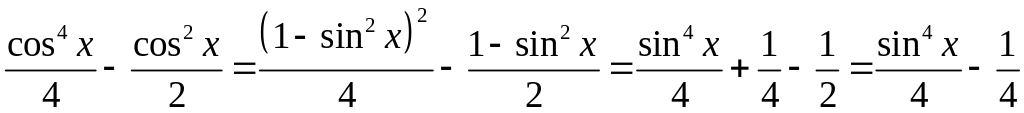 .
.
Якщо
примінити підстановку
![]() ,
то інтеграл значно ускладнюється.
Дійсно,
,
то інтеграл значно ускладнюється.
Дійсно,
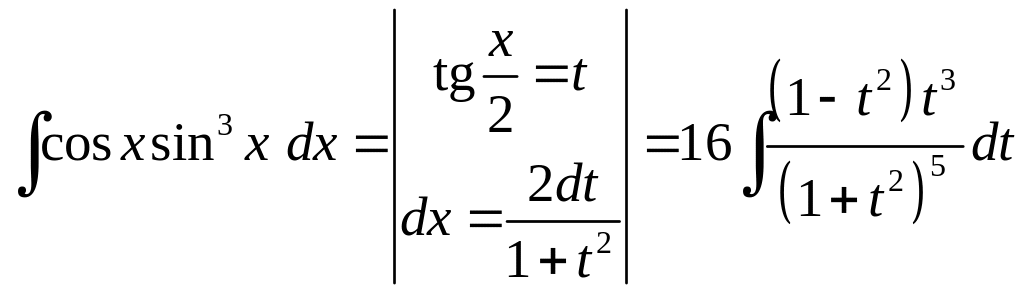 .
.
Оскільки
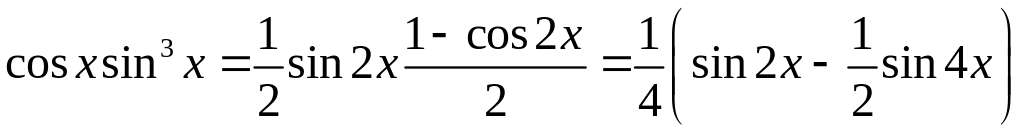 ,
то
,
то
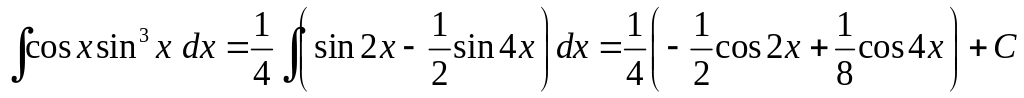 .
.
Розібраний приклад показує, що на відміну від операції диференціювання функції операція інтегрування є більш складною, але і більш захоплюючою і можна цілком перефразувати слова М. Ломоносова, що інтегрування функції "розум до ладу приводить".
3. Інтеграли від деяких ірраціональних виразів Розглянемо інтеграл виду
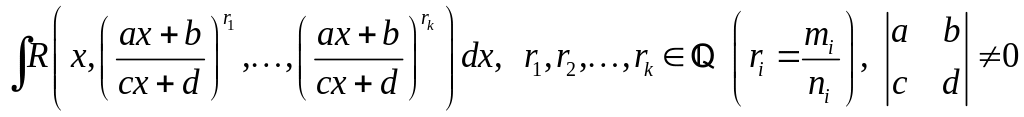 (4.3)
(4.3)
Якщо
![]() загальний
знаменник раціональних чисел
загальний
знаменник раціональних чисел
![]() ,
то підстановка
,
то підстановка
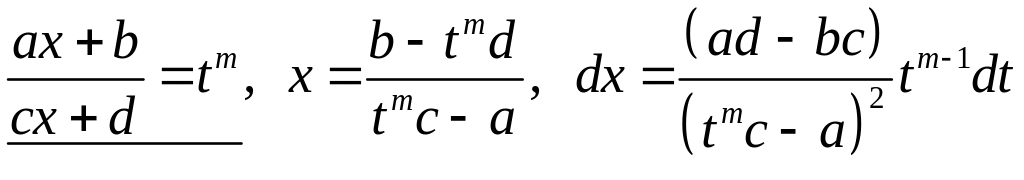
раціоналізує
інтеграл (4.3). Дійсно, як видно,
![]() раціональні
функції від
раціональні
функції від
![]() і
і
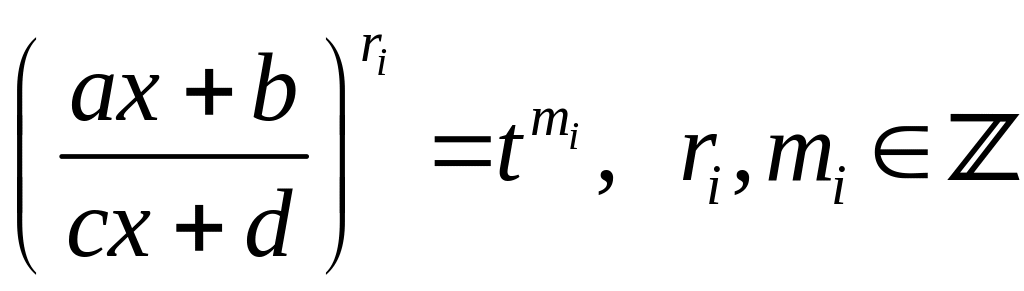 .
.
Зокрема,
1) якщо
![]() ,
тобто
,
тобто
![]() ,
,
то інтеграл
раціоналізується підстановкою
![]() де
загальний
знаменник дробів
;
де
загальний
знаменник дробів
;
2) Якщо
![]() ,
тобто
,
тобто
![]() , (4.4)
, (4.4)
то інтеграл
(4.4) раціоналізується підстановкою
![]() де
загальний
знаменник дробів
;
де
загальний
знаменник дробів
;
Приклад 4.10.
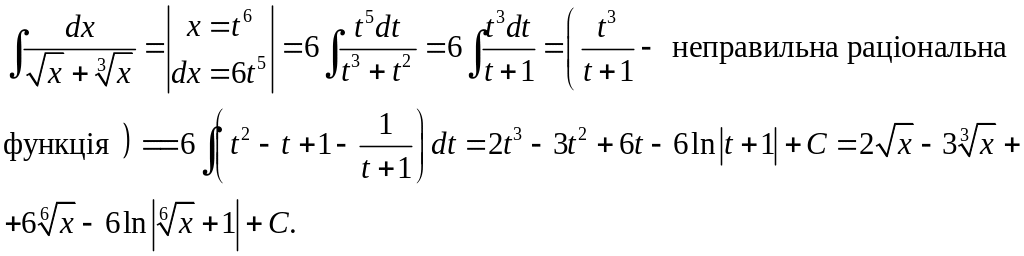
Але інтеграли виду
![]()
вже не
раціоналізуються підстановкою
![]() ,
тому що при цьому
не виражається раціональним чином через
.
Тут будемо робити інакше. Виділимо
повний квадрат під коренем
,
тому що при цьому
не виражається раціональним чином через
.
Тут будемо робити інакше. Виділимо
повний квадрат під коренем
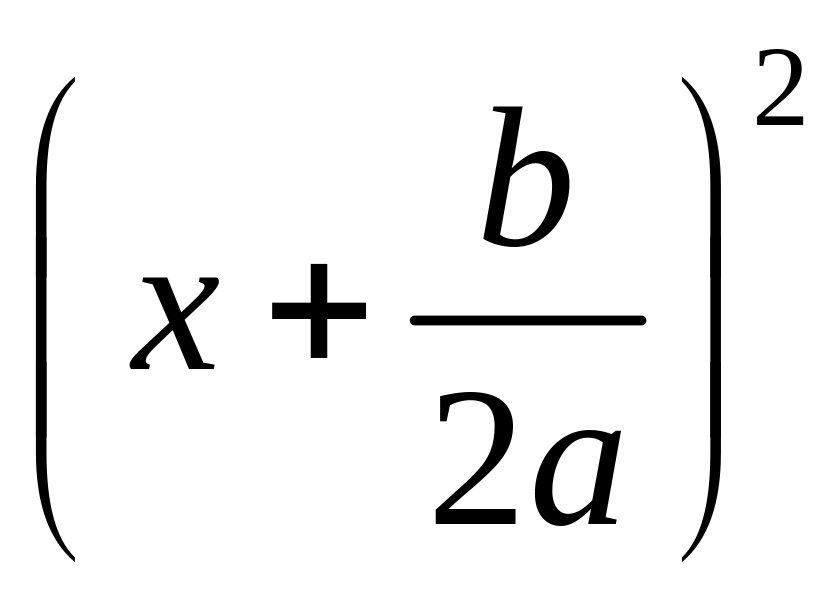 ,
заміною
,
заміною
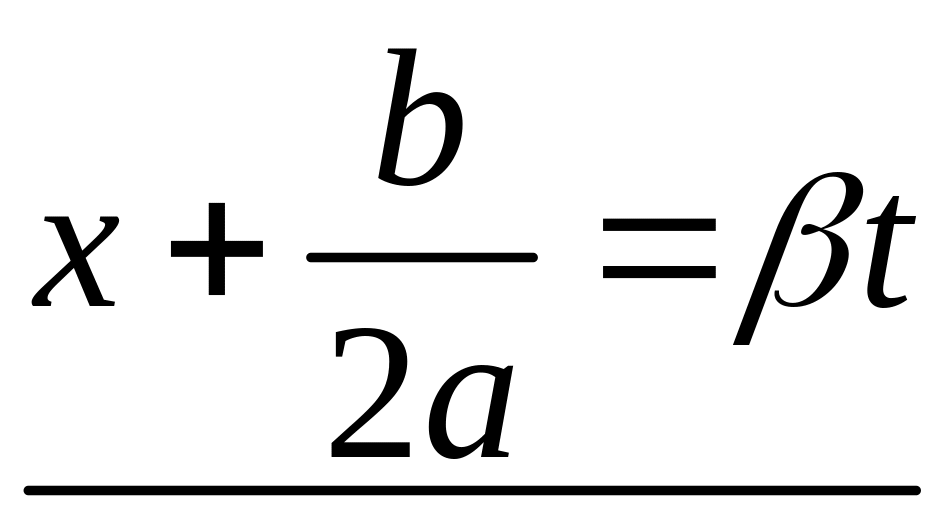 ,
де
,
де
![]() спеціально
підібрана
спеціально
підібрана
![]() ,
приведемо квадратний корінь до одного
з можливих виразів
,
приведемо квадратний корінь до одного
з можливих виразів
![]() .
.
Тоді
![]()
підстановкою
![]() (або
(або
![]() )
зводиться до
)
зводиться до
![]() ,
який розглядався вище.
,
який розглядався вище.
