
- •С. Б. Волкова математическая статистика и планирование эксперимента
- •§ 2. Интервальные оценки . . . . . . . . . . . . . . . . . . . . . . . . . 50
- •§ 3. Проверка статистических гипотез . . . . . . . . . . . . . . . . 58
- •§ 2. Доверительные интервалы для параметров
- •§ 3. Полные факторные эксперименты типа 2k.
- •§ 4. Оптимизация планов. Поиск экстремума
- •Предисловие
- •Введение
- •§ 1. Математическая модель статистического эксперимента
- •§ 2. Случайные величины
- •Глава 1. Элементы математической статистики
- •§ 1. Выборочный метод. Точечные оценки
- •§ 2. Интервальные оценки
- •§ 3. Проверка статистических гипотез
- •2. Проверка гипотезы о равенстве дисперсий двух нормально распределенных случайных величин.
- •§ 4. Однофакторный дисперсионный анализ
- •§ 5. Элементы теории корреляции
- •Глава 2. Планирование эксперимента
- •§ 1. Пассивный эксперимент
- •7. Оценивание функции отклика и ее параметров.
- •§ 2. Доверительные интервалы для параметров функции отклика и гипотеза адекватности
- •§ 3. Полные факторные эксперименты типа 2k . Анализ факторных экспериментов
- •4. Насыщенное и ненасыщенное планирование.
- •§ 4. Оптимизация планов. Поиск экстремума функции отклика
- •Для распределения 2 с n степенями свободы
- •Критические точки критерия 2:
- •Критические точки критерия 2:
- •Литература для дополнительного чтения
- •Светлана Борисовна Волкова математическая статистика и планирование эксперимента
- •162600, Г. Череповец, пр. Луначарского, 5.
2. Проверка гипотезы о равенстве дисперсий двух нормально распределенных случайных величин.
Определение. Случайная величина Fmn называется распределенной по закону Фишера со степенями свободы m и n, если она представляется в виде
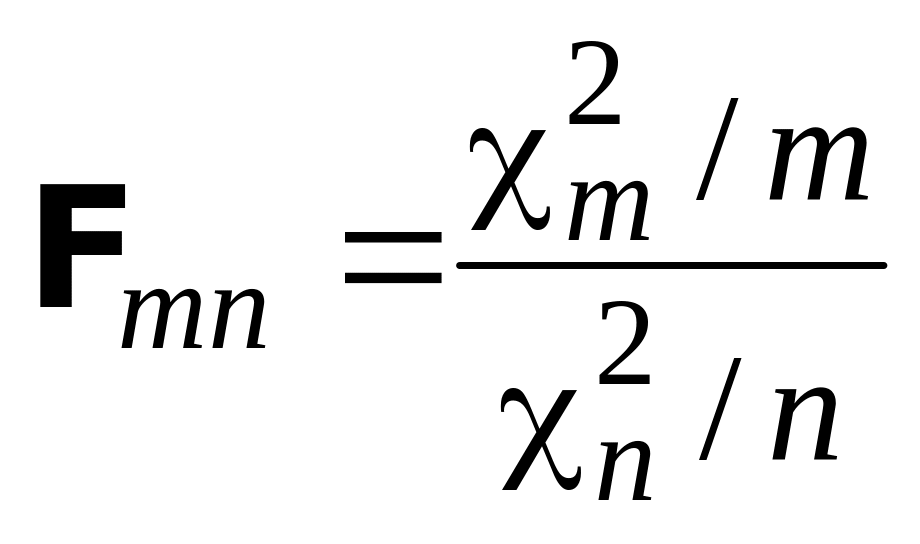 ,
,
где
![]() и
и
![]() – независимые случайные величины,
распределенные по закону 2
с m и n
степенями свободы соответственно.
– независимые случайные величины,
распределенные по закону 2
с m и n
степенями свободы соответственно.
Рассмотрим две
независимые случайные величины
и , распределенные
по нормальному закону с дисперсиями
![]() и
и
![]() ,
которые предполагаются неизвестными.
Пусть в результате наблюдений получены
выборка
,
которые предполагаются неизвестными.
Пусть в результате наблюдений получены
выборка
![]() значений x и выборка
значений x и выборка
![]() значений ,
значений ,
![]() и
и
![]() – исправленные выборочные дисперсии,
соответствующие этим выборкам. Обозначим
– исправленные выборочные дисперсии,
соответствующие этим выборкам. Обозначим
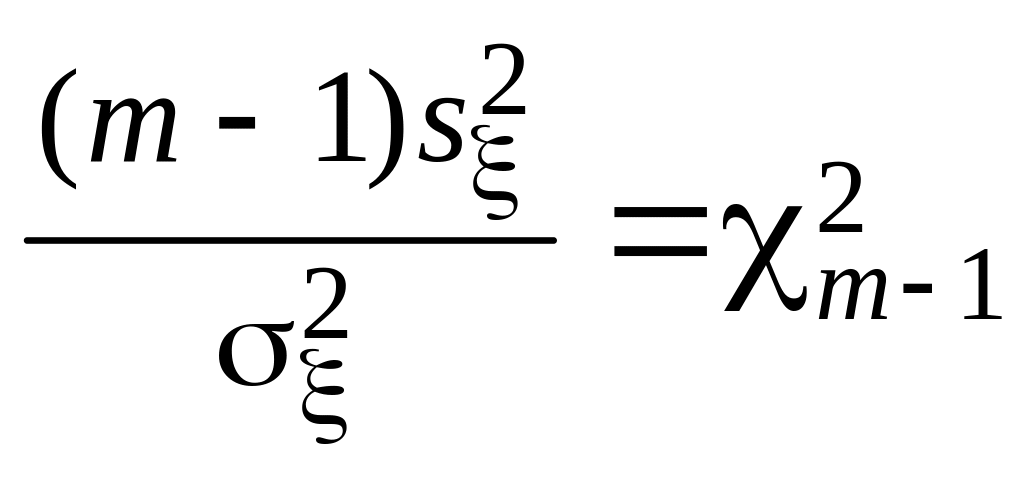 и
и
 ,
(1)
,
(1)
тогда
![]() и
и
![]() – случайные величины, распределенные
по закону 2
со степенями свободы соответственно
m – 1 и n
– 1 (см. § 2, п. 3 (в)).
Из независимости
и следует, что
случайные величины (1) также независимы.
В соответствии с определением случайная
величина
– случайные величины, распределенные
по закону 2
со степенями свободы соответственно
m – 1 и n
– 1 (см. § 2, п. 3 (в)).
Из независимости
и следует, что
случайные величины (1) также независимы.
В соответствии с определением случайная
величина
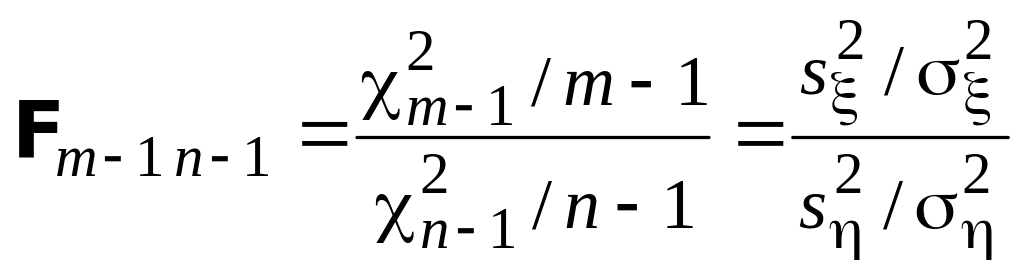 (2)
(2)
распределена по закону Фишера со степенями свободы m – 1 и n – 1.
Теперь мы можем
построить критерий для проверки гипотезы
H0:
![]() .
.
Если эта гипотеза верна, то из (2) получаем
![]() .
(3)
.
(3)
Случайную величину (3) и используют в качестве критерия для проверки гипотезы H0. Рассмотрим
Случай 1:
![]() и
и
![]() заметно различаются и при этом
>
.
В этом случае используется альтернативная
гипотеза HА:
заметно различаются и при этом
>
.
В этом случае используется альтернативная
гипотеза HА:
![]() .
Вычисляют
.
Вычисляют
![]() ,
затем по таблице критических точек
распределения Фишера по уровню значимости
и числам степеней
свободы m – 1 и n
– 1 отыскивается критическая точка
Fкр(,
m – 1, n – 1).
,
затем по таблице критических точек
распределения Фишера по уровню значимости
и числам степеней
свободы m – 1 и n
– 1 отыскивается критическая точка
Fкр(,
m – 1, n – 1).
Если Fнабл < Fкр, то основную гипотезу принимают; если же Fнабл > Fкр, то основную гипотезу отвергают.
Если
<
,
то можно аналогично использовать
левостороннюю критическую область, но
обычно, поскольку таблица не содержит
соответствующих критических точек,
снова используют правостороннюю
критическую область, взяв в качестве
критерия обратное отношение
![]() .
.
Случай 2:
и
различаются мало, тогда в качестве
альтернативной берется гипотеза HА:
![]() .
По уровню значимости /2
и числам степеней свободы m
– 1 и n – 1 (m – 1
– число степеней свободы распределения
с бóльшей выборочной дисперсией) ищут
.
По уровню значимости /2
и числам степеней свободы m
– 1 и n – 1 (m – 1
– число степеней свободы распределения
с бóльшей выборочной дисперсией) ищут
![]() ( / 2, m – 1, n – 1),
а затем
( / 2, m – 1, n – 1),
а затем
![]() .
.
Если
![]() < Fнабл
<
< Fнабл
<
![]() ,
основную гипотезу принимают, а при
Fнабл
<
или Fнабл
>
ее отвергают.
,
основную гипотезу принимают, а при
Fнабл
<
или Fнабл
>
ее отвергают.
Пример 1.
Получены выборки значений двух независимых
случайных величин, распределенных по
нормальному закону. Объемы выборок m
11 и
n
14, исправленные выборочные дисперсии
![]() и
и
![]() .
Требуется проверить при уровне значимости
0,05
гипотезу H0: D
D
при альтернативной гипотезе HA:
D
D.
.
Требуется проверить при уровне значимости
0,05
гипотезу H0: D
D
при альтернативной гипотезе HA:
D
D.
Здесь
![]() .
По таблице критических точек распределения
Фишера находим
(0,025;
10; 13) 3,25, откуда
.
По таблице критических точек распределения
Фишера находим
(0,025;
10; 13) 3,25, откуда
![]() .
Так как
< Fнабл
<
,
то нет оснований отвергать гипотезу
о равенстве дисперсий. Другими словами,
выборочные дисперсии различаются
незначимо.
.
Так как
< Fнабл
<
,
то нет оснований отвергать гипотезу
о равенстве дисперсий. Другими словами,
выборочные дисперсии различаются
незначимо.
Пример 2.
По двум выборкам, объемы которых m
10 и n
18, найдены
исправленные выборочные дисперсии
![]() и
и
![]() .
При уровне значимости 0,05
требуется проверить гипотезу H0:
D
D,
взяв в качестве альтернативной гипотезу
HA:
D
> D.
.
При уровне значимости 0,05
требуется проверить гипотезу H0:
D
D,
взяв в качестве альтернативной гипотезу
HA:
D
> D.
Здесь критическая
область является правосторонней. По
таблице критических точек распределения
Фишера находим критическую точку:
![]() (0,05;
9; 17) 2,50. Поскольку
(0,05;
9; 17) 2,50. Поскольку
![]() >
,
выборочные дисперсии различаются
значимо. Гипотеза о равенстве дисперсий
отвергается.
>
,
выборочные дисперсии различаются
значимо. Гипотеза о равенстве дисперсий
отвергается.
3. Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин с равными неизвестными дисперсиями. Пусть нормально распределенные случайные величины и независимы и их дисперсии неизвестны. По выборкам малого объема (меньше 30) нельзя получить хорошие оценки дисперсий. Но если предположить, что D D, то оказывается, что можно построить критерий Стьюдента для сравнения математических ожиданий. (Если нет уверенности, что дисперсии одинаковы, то, прежде чем сравнивать математические ожидания, следует с помощью критерия Фишера предварительно проверить гипотезу о равенстве дисперсий.)
Обозначим D
D
2,
M
a,
M
b.
Пусть получены выборки
и
значений соответственно x
и ,
![]() и
и
![]() – определяемые этими выборками
эмпирические математические ожидания,
– определяемые этими выборками
эмпирические математические ожидания,
![]() и
и
![]() – исправленные эмпирические дисперсии.
Так как случайные величины x
и независимы, то
и
также являются независимыми случайными
величинами и притом распределенными
по нормальному закону. Отсюда следует,
что разность
– исправленные эмпирические дисперсии.
Так как случайные величины x
и независимы, то
и
также являются независимыми случайными
величинами и притом распределенными
по нормальному закону. Отсюда следует,
что разность
![]() распределена по нормальному закону.
При этом имеем
распределена по нормальному закону.
При этом имеем
![]() ,
,
![]() ,
поэтому случайная величина
,
поэтому случайная величина
![]() распределена по нормальному закону,
причем M0
0, D0
1.
распределена по нормальному закону,
причем M0
0, D0
1.
Из независимости
x и
следует независимость случайных величин
![]() и
и
![]() ,
которые распределены по закону 2
со степенями свободы соответственно
m – 1 и n
– 1 (см. § 2, п. 3 (в)).
Следовательно, случайная величина
,
которые распределены по закону 2
со степенями свободы соответственно
m – 1 и n
– 1 (см. § 2, п. 3 (в)).
Следовательно, случайная величина
![]() распределена по закону
с m
n – 2 степенями
свободы (§ 2, п. 3 (б)).
Но тогда случайная величина
распределена по закону
с m
n – 2 степенями
свободы (§ 2, п. 3 (б)).
Но тогда случайная величина
![]() (4)
(4)
распределена по закону Стьюдента с m n – 2 степенями свободы.
Теперь построим критерий для проверки гипотезы H0: M M, т. е. a b.
Если эта гипотеза верна, то (4) приводится к равенству
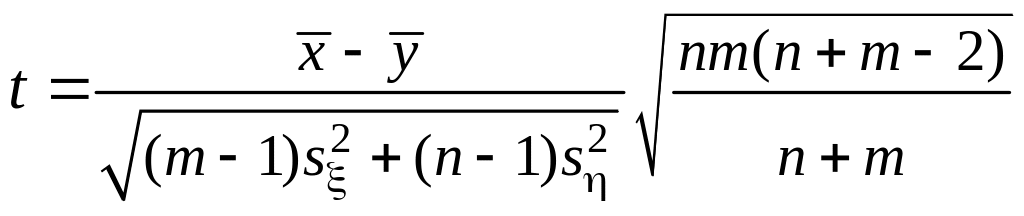 .
(5)
.
(5)
Случайная величина (5) и является критерием для проверки гипотезы H0.
Случай 1: альтернативная гипотеза a b. В этом случае строится двусторонняя критическая область такая, чтобы вероятность попадания значения t в эту область в случае справедливости основной гипотезы была равна принятому уровню значимости .
Поскольку плотность
вероятностей распределения Стьюдента
– четная функция (см. § 2, п. 3),
критические точки симметричны относительно
нуля. Поэтому достаточно найти правую
критическую точку. Ее находят по таблице
критических точек распределения
Стьюдента по уровню значимости / 2
и k
m +
n – 2
(![]() ).
).
Если
![]() ,
то основную гипотезу принимают.
,
то основную гипотезу принимают.
Если
![]() ,
то основную гипотезу отвергают.
,
то основную гипотезу отвергают.
Случай 2:
альтернативная гипотеза a
> b. Строится
правосторонняя критическая область.
Единственную критическую точку находят
по уровню значимости
и числу степеней свободы n + m – 2
в таблице критических точек распределения
Стьюдента:
![]() .
.
Если
![]() ,
то основная гипотеза принимается.
,
то основная гипотеза принимается.
Если
![]() ,
то основную гипотезу отвергают.
,
то основную гипотезу отвергают.
Случай 3:
альтернативная гипотеза a
< b. В этом случае
строится левосторонняя критическая
область. Критическая точка
![]() .
.
Если , то основная гипотеза принимается.
Если , то основную гипотезу отвергают.
Пример. В
ряде экспериментов исследовалось
влияние CaO как активатора
расширения ангидритовых растворов.
Было изготовлено две серии пробных
образцов по 6 штук каждая. Серия 0 (нулевая
проба) не содержала CaO;
серия 1 содержала 1% CaO. По
результатам исследований получено:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]() ,
т. е. имеются точечные оценки параметров
двух случайных величин: 0
– расширения раствора, не содержащего
CaO, и 1
– расширения раствора, содержащего
CaO.
,
т. е. имеются точечные оценки параметров
двух случайных величин: 0
– расширения раствора, не содержащего
CaO, и 1
– расширения раствора, содержащего
CaO.
Выясним, значимо ли различие между обоими средними. Для этого проверим гипотезу M0 M1 при уровне значимости 0,05 и альтернативной гипотезе M0 M1.
Так как обе выборки
имеют малый объем, то сначала нужно
проверить гипотезу о равенстве их
дисперсий. В этом случае воспользуемся
односторонним критерием, так что
конкурирующая гипотеза будет иметь
вид: D
> D
По таблице критических точек распределения
Фишера по уровню значимости 0,05
и числам степеней свободы
![]() находим
находим
![]() .
Так как
.
Так как
![]() ,
то исправленные выборочные дисперсии
отличаются незначимо. Далее вычисляем
,
то исправленные выборочные дисперсии
отличаются незначимо. Далее вычисляем
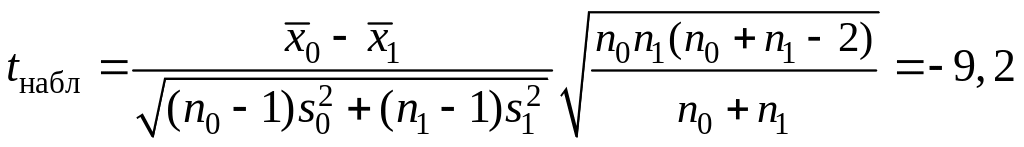 и по таблице критических точек
распределения Стьюдента по уровню
значимости a / 2
0,025 и числу степеней свободы
и по таблице критических точек
распределения Стьюдента по уровню
значимости a / 2
0,025 и числу степеней свободы
![]() получаем
получаем
![]() .
Так как
,
то основная гипотеза отвергается,
другими словами, различие между средними
значимо. Таким образом, влияние CaO
как активатора расширения ангидритовых
растворов существенно.
.
Так как
,
то основная гипотеза отвергается,
другими словами, различие между средними
значимо. Таким образом, влияние CaO
как активатора расширения ангидритовых
растворов существенно.
4. Эмпирические и теоретические кратности. Пусть имеются основания предполагать, что случайная величина распределена по некоторому определенному закону. Это предположение можно проверить, сравнивая эмпирические и теоретические кратности. Рассмотрим
Случай 1:
предполагаемое распределение дискретно.
Пусть в результате n
испытаний случайная величина
приняла nj
раз значение zj
( j
1, 2, ..., m; n1
+ n2 + ... + + nm
n). Найдем вероятности
pj
значений zj,
считая, что имеет
предполагаемое распределение, и положим
![]() ( j
1, 2, ..., m). Числа
( j
1, 2, ..., m). Числа
![]() назовем теоретическими кратностями
значений zj
в выборке объема n.
Сравнение теоретических кратностей
назовем теоретическими кратностями
значений zj
в выборке объема n.
Сравнение теоретических кратностей
![]() с эмпирическими (наблюдаемыми) кратностями
nj
дает возможность принять или отвергнуть
гипотезу о распределении случайной
величины по
предполагаемому закону.
с эмпирическими (наблюдаемыми) кратностями
nj
дает возможность принять или отвергнуть
гипотезу о распределении случайной
величины по
предполагаемому закону.
Случай 2: предполагаемое распределение является непрерывным. Тогда вероятности отдельных значений x равны нулю. В этом случае промежуток, содержащий все значения , разбивают на m непересекающихся промежутков одной той же длины h и вычисляют вероятности pj попадания значения в j-й промежуток, а затем, как и в случае дискретного распределения, сравнивают теоретические кратности с наблюдаемыми кратностями nj.
В частности, если
случайная величина
имеет непрерывную плотность вероятностей
f, то, обозначая через
yj
и yj
+ h концы j-го
промежутка, получаем
![]()
![]() ,
откуда следует
,
откуда следует
![]() .
.
Близость теоретических кратностей к наблюдаемым подтверждает гипотезу о предполагаемом распределении случайной величины .
5. Проверка гипотезы о нормальном распределении. Критерий согласия Пирсона. Критерий для проверки гипотезы о предполагаемом законе неизвестного распределения называют критерием согласия. Одним из критериев согласия является критерий Пирсона, который можно применять для проверки различных гипотез о законе распределения случайной величины. Для построения критерия числовая прямая разбивается на несколько промежутков и устанавливается наблюдаемое и теоретическое число значений случайной величины, попадающее в каждый промежуток. Обычно они различаются. Это различие может быть случайным (незначимым) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Может оказаться, что это различие не случайно (значимо) и объясняется тем, что теоретические кратности вычислены исходя из неверной гипотезы.
Здесь будет рассмотрено применение критерия Пирсона для проверки гипотезы о нормальном распределении.
Пусть имеется выборка значений случайной величины объема n. Отрезок, концами которого являются наименьшая и наибольшая варианты, содержит все числа этой выборки. Разобьем этот отрезок на m частичных промежутков одинаковой длины:
[ y1; y2), [ y2; y3), [ y3; y4), ..., [ ym–1; ym), [ ym; ym+1] (6)
(общие концы двух соседних промежутков отнесены к правому промежутку). Обозначим через nj – число элементов выборки, попавших в j-й промежуток (n1 + n2 + ... + nm n). Поскольку y1 и ym+1 – наименьшая и наибольшая варианты, то крайние промежутки последовательности (6) можно заменить промежутками (–; y2) и [ym; ), не меняя значений n1 и nm. Таким образом, мы получаем последовательность промежутков
(–; y2), [ y2; y3), [ y3; y4), ..., [ym–1; ym), [ym; ), (7)
объединение которых
– вся числовая прямая. При этом n1,
n2, ..., nm
являются количествами чисел имеющейся
выборки, попавшими в эти промежутки.
Наряду с этими наблюдаемыми количествами
можно построить теоретические в
предположении, что случайная величина
распределена по
нормальному закону. Для этого введем в
рассмотрение числа
![]() (середины промежутков последовательности
(6)). Эти числа называют равноотстоящими
вариантами, полученными группировкой
выборки. Приписывая им в качестве
кратностей числа nj,
получим следующий закон распределения
(середины промежутков последовательности
(6)). Эти числа называют равноотстоящими
вариантами, полученными группировкой
выборки. Приписывая им в качестве
кратностей числа nj,
получим следующий закон распределения
|
|
... |
|
|
|
... |
|
Математическим ожиданием и дисперсией этого распределения являются числа
![]() ,
,
![]() ,
(8)
,
(8)
которые называют
выборочными математическим ожиданием
и дисперсией, полученными группировкой
выборки. При большом n
эти числа мало отличаются от
и
![]() .
.
Рассматривая числа
![]() и
и
![]() как приближенные значения математического
ожидания и квадратичного отклонения
случайной величины
и предполагая, что эта случайная величина
распределена по нормальному закону,
найдем вероятности того, что ее значения
попадают в промежутки (7). По формуле
(5) из § 2 Введения получаем
как приближенные значения математического
ожидания и квадратичного отклонения
случайной величины
и предполагая, что эта случайная величина
распределена по нормальному закону,
найдем вероятности того, что ее значения
попадают в промежутки (7). По формуле
(5) из § 2 Введения получаем
![]() ;
;
![]()
при j 2, 3, ..., m – 1;
![]() ,
,
где
![]() ;
;
![]() .
.
Теоретические
кратности находят по формуле:
![]() .
.
Рассмотрим теперь случайную величину
 ,
,
которая, как доказал Пирсон, распределена по закону 2 c m – 3 степенями свободы.
Ясно, что, чем меньше различаются числа nj и nj, тем меньше наблюдаемое значение этой случайной величины. Поэтому ее можно использовать для проверки гипотезы о нормальном распределении данной случайной величины .
Построим
правостороннюю критическую область,
исходя из требования, чтобы вероятность
попадания значения критерия в эту
область в предположении справедливости
основной гипотезы равнялась принятому
уровню значимости .
Критическая точка
![]() удовлетворяет условию
удовлетворяет условию
![]() и находится по таблице критических
точек распределения 2.
и находится по таблице критических
точек распределения 2.
Если
![]() ,
то основную гипотезу принимают.
,
то основную гипотезу принимают.
Если
![]() ,
то нулевую гипотезу отвергают.
,
то нулевую гипотезу отвергают.
Пример. Получена выборка значений случайной величины объема n 190. Найденные значения распределены по промежуткам следующим образом.
Промежуток |
[4; 6) |
[6; 8) |
[8; 10) |
[10; 12) |
[12; 14) |
Количество |
n1 15 |
n2 26 |
n3 25 |
n4 30 |
n5 26 |
Промежуток |
[14; 16) |
[16; 18) |
[18; 20) |
[20; 22] |
Количество |
n6 14 |
n7 16 |
n8 18 |
n9 20 |
Проверим гипотезу о нормальном распределении .
Находим равноотстоящие варианты:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
По формулам (8) получаем 12,6, 4,93.
Вычисление чисел
![]() проведено с помощью расчетной таблицы,
приведенной на стр. 72.
проведено с помощью расчетной таблицы,
приведенной на стр. 72.
j |
yj |
|
(zj) |
pj (zj+1) – (zj) |
190pj |
1 |
– |
– |
–0,5 |
0,0901 |
17,119 |
2 |
6 |
– 1,34 |
–0,4099 |
0,0861 |
16,359 |
3 |
8 |
– 0,93 |
–0,3238 |
0,1219 |
23,161 |
4 |
10 |
– 0,53 |
–0,2019 |
0,1541 |
29,279 |
5 |
12 |
– 0,12 |
–0,0478 |
0,1581 |
30,039 |
6 |
14 |
0,28 |
0,1103 |
0,1446 |
27,474 |
7 |
16 |
0,69 |
0,2549 |
0,1094 |
20,786 |
8 |
18 |
1,10 |
0,3643 |
0,0689 |
13,091 |
9 |
20 |
1,50 |
0,4332 |
0,0668 |
12,692 |
10 |
|
|
0,5 |
|
|
|
|
Контроль: |
|
|
|
Отсюда следует
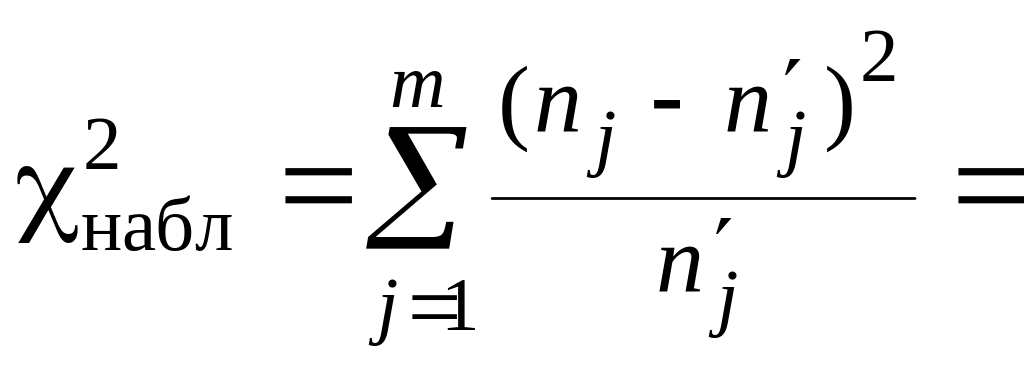 20,41,
а по таблице критических точек
распределения 2
(табл. 3) находим
20,41,
а по таблице критических точек
распределения 2
(табл. 3) находим
![]() .
Так как
.
Так как
![]() ,
гипотеза о нормальном распределении
отвергается.
,
гипотеза о нормальном распределении
отвергается.
При использовании критерия Пирсона объем выборки должен быть не менее 50 и каждая группа должна содержать не менее пяти чисел выборки.
