Глава 2. Планирование эксперимента

§ 1. Пассивный эксперимент

1. Факторы. При экспериментальных исследованиях имеют дело с объектами исследований. Объектами исследований могут быть приборы, технологические линии, изделия и т. д. Обычно требуется установить связь между входными и выходными переменными объекта.

Входные переменные называют факторами. Они разбиваются на два основных класса: контролируемые (измеряемые) и неконтролируемые (неизмеряемые). Будем предполагать, что входные переменные измеряются точно. Конечно, измерения контролируемых переменных происходят с ошибками, но ими обычно в эксперименте пренебрегают.

Контролируемые переменные могут быть управляемыми и неуправляемыми. Управляемыми называются переменные, которые в эксперименте можно целенаправленно изменять. Переменные, для которых такое изменение невозможно, называются неуправляемыми. Например, при исследовании технологического процесса контролируемыми переменными являются регистрируемые по показаниям приборов переменные, характеризующие состояние этого процесса. Управляемыми переменными в этом случае будут переменные, с помощью которых происходит целенаправленное изменение технологического процесса.

Контролируемые переменные бывают качественными и количественными. Например, при исследовании влияния разных типов наполнителей бетона на его выходные характеристики тип наполнителя является качественным фактором, т. к. его нельзя оценить количественно.

Примерами неконтролируемых переменных могут служить: неконтролируемые примеси в составе исходного сырья, различные возмущения внешней среды и т. д. Обычно влияние случайных воздействий на объект незначительно, но существует группа неконтролируемых переменных, воздействие которых на объект довольно существенно и не обязательно случайно. О существовании этих переменных мы либо ничего не знаем, либо знаем, но почему-либо не можем их измерить.

Пусть v  (v₁, v₂, ..., ) – вектор входных контролируемых управляемых переменных; u  (u₁, u₂, ..., ) – вектор входных контролируемых неуправляемых переменных; z  ( z₁, z₂, ..., z_m) – вектор входных неконтролируемых переменных; y  ( y₁, y₂, ..., y_r) – вектор выходных переменных. Тогда вектор входных контролируемых переменных запишется в виде x  (v, u)  (v₁, v₂, ..., u₁, u₂, ..., ), а , где – вектор‑функция от k₁ + k₂ + m переменных. Если z – случайный вектор, то при любом фиксированном x выходная переменная y есть также случайный вектор. Его обычно называют откликом.

Если над данным объектом проведено N испытаний, то последовательность (( y₁, x₁), ( y₂, x₂), ..., ( y_N, x_N)), в которой x_j – значение, принимаемое входной переменной x в j‑м испытании, а y_j  (x_j, z) ( j 1, 2, ..., N), принято называть _N -экспериментом.

Замечание. В дальнейшем изложении любой вектор отождествляется с одностолбцовой матрицей, так что если x  ( x₁, x₂, ..., x_n), то также пишем 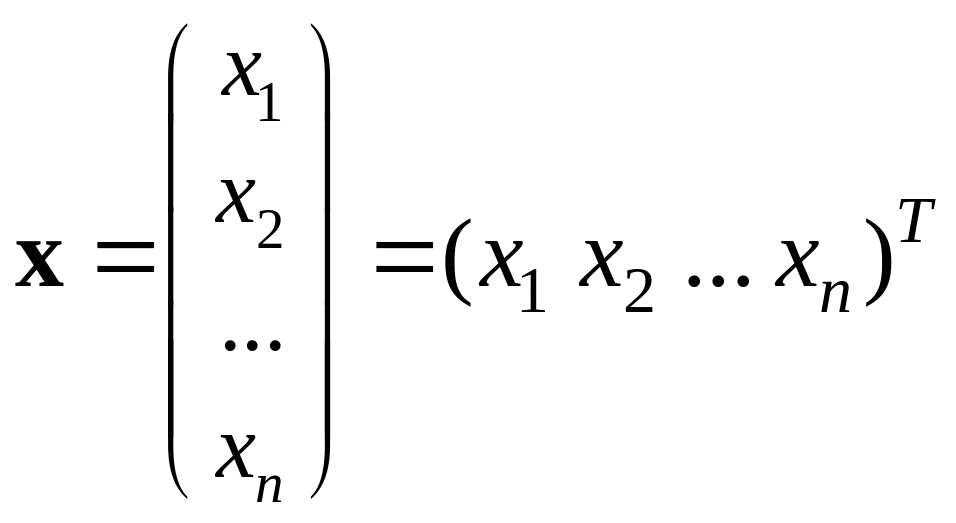(верхний индекс T означает транспонирование матрицы). В связи с этим одностолбцовая матрица будет часто называться вектор-столбцом.

2. Линейная модель наблюдений. Пусть имеется n наблюдений (случайных величин) , для которых

, i  1, 2, ..., n; (1)

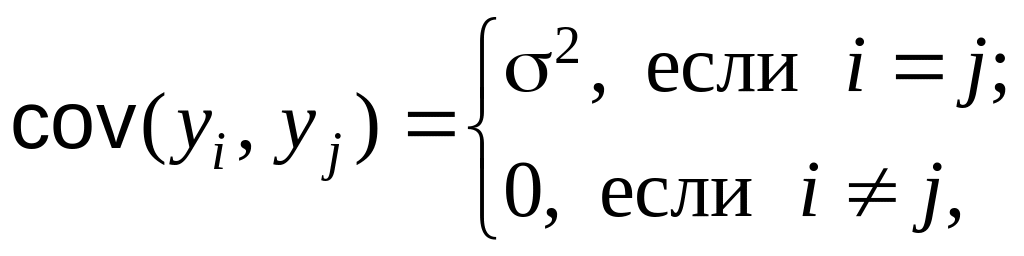(2)

где и – неизвестные параметры, x_ij – известные коэффициенты, cov ( y_i, y_j) – ковариация между y_i и y_j (Введение, § 2, п. 6).

Условие (2) является требованием некоррелированности случайных величин и равенства дисперсий всех .

Пусть X  (x_ij) – матрица неизвестных коэффициентов (порядка n  p), – вектор-столбец наблюдений; , Dy  (cov ( y_i, y_j)) – ковариационная матрица наблюдений, – вектор-столбец неизвестных параметров. Тогда равенства (1) и (2) можно переписать в матричном виде:

, , (3)

где – единичная матрица порядка n.

Положим

, i  1, 2, ..., n;

тогда

, (4)

или, в матричной записи, полагая ,

y  Xβ. (5)

Так как M_i  0 и cov (_i, _j)  M(_i_j) – M_iM_j   M(( y_i – My_i)M( y_j – My_j))  cov ( y_i, y_j), то, учитывая (3) и (4), имеем

, , (6)

где 0 – нулевой вектор-столбец.

Равенство (5) называют линейной (по параметру β) моделью наблюдений. Равенство (5) с условиями (6) называют линейной моделью с некоррелированными наблюдениями.

Неизвестные параметры называют коэффициентами регрессии.

Пример. Пусть – уравнение движения объекта, в котором параметры неизвестны. В моменты времени измеряется его координата . Обозначим наблюдаемое значение координаты в момент времени (i  1, 2, ..., n). Ошибкой наблюдения в момент времени является (i  1, 2, ..., n), так что  . Предположим, что ошибки наблюдений _i – попарно некоррелированные случайные величины, имеющие одинаковые дисперсии и нулевое среднее. Полагая (i  1, 2, ..., n; j  1, 2, ..., p), получим линейную модель наблюдений вида (4), удовлетворяющую условиям:

M_i  0,

3. Оценивание коэффициентов регрессии методом наименьших квадратов. Рассмотрим задачу оценивания коэффициентов регрессии по наблюдениям , удовлетворяющим условиям (3). Как было сказано в п. 6 § 1 гл. 1, точечная оценка параметра представляет собой действительную функцию от наблюдений: . Введем следующее

Определение 1. Оценка параметра _j называется линейной, если f_j представляет собой линейную форму от .

Таким образом, если оценки всех _j линейны, имеем

( j   1, 2, ..., p).

В этом случае будем также говорить, что вектор-столбец есть линейная оценка вектор-столбца коэффициентов регрессии .

Рассмотрим выражение

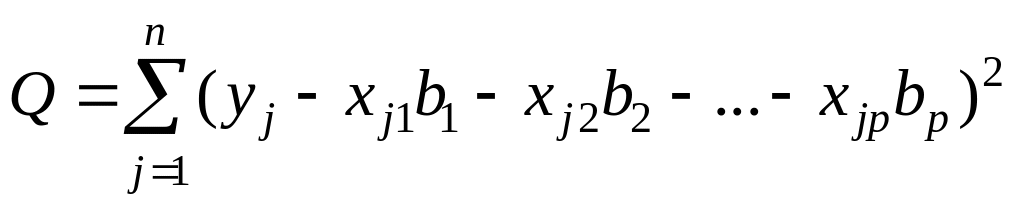, (7)

где – переменные, принимающие любые действительные значения.

Определение 2. Значения , минимизирующие функцию (7) при наблюдаемых значениях , называются оценками метода наименьших квадратов или, коротко, МНК-оценками неизвестных параметров _j.

Необходимые условия МНК-оценки параметра задаются равенствами:

(k  1, 2, ..., p),

которые можно переписать в виде , или, в матричной форме,

. (8)

Таким образом, если МНК-оценка существует, то она принадлежит множеству решений уравнения (8). Можно доказать, что верно и обратное: любое решение уравнения (8) является МНК-оценкой параметра β (см., например, [1], п. 1.1.2). Уравнение (8) называют нормальным. Можно показать, что оно всегда имеет решение притом, что уравнение может быть несовместным.

Если ранг матрицы равен p, т. е. числу неизвестных параметров _j, то ранг матрицы также равен p и поскольку S – квадратная матрица порядка p, то она является невырожденной, но тогда существует обратная матрица и, следовательно, нормальное уравнение имеет в этом случае единственное решение , которое находится по формуле

. (9)

При этом, используя (3), получаем , т. е. при  j  1, 2, ..., p, так что все оценки являются несмещенными.

4. Матрица ковариаций оценок, полученных методом наименьших квадратов. Нам понадобится следующая

Лемма. Пусть x  (x₁, x₂, ..., x_n) – случайный вектор (отождествляемый со столбцовой матрицей), A  (a_ij) – матрица линейного преобразования порядка mn и y  Ax.

Тогда дисперсии Dx  (соv (x_i, x_j)) и Dy  (соv (y_i, y_j)) связаны равенством Dy  ADxA^T.

Доказательство. Для произвольной матрицы M будем обозначать элемент, стоящий в i-й строке и j-м столбце, через (M)_ij. Получаем

(Dy)_ij  соv (y_i, y_j)  M((y_i – My_i)(y_j – My_j)) 



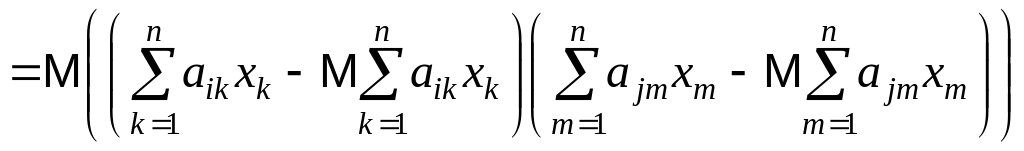
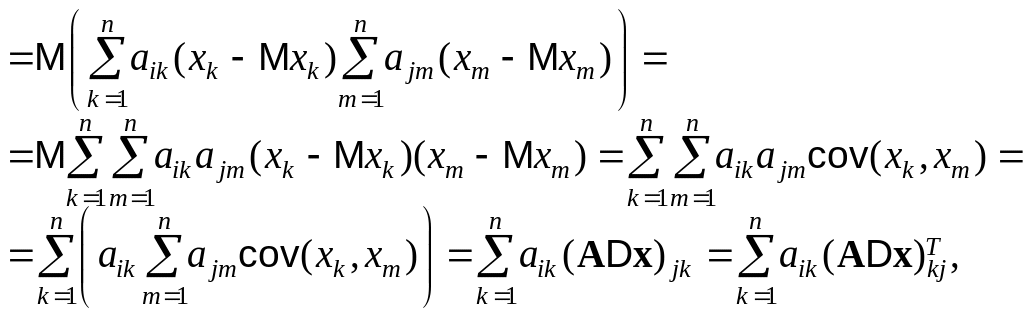
откуда Dy  A(ADx)^T  ADxA^T (последнее равенство следует из того, что (AB)^T  B^TA^T для любых матриц A и B, и очевидного равенства (Dx)^T  Dx).

Применим теперь полученный результат к ковариационной матрице МНК-оценок, определяемых формулой (9). Используя (9) и (3), получаем . Так как , то матрица симметрична, следовательно, обратная матрица S^–1 также симметрична, поэтому имеем окончательно

(10)

Заметим, что оценки в общем случае коррелированы. Однако имеет место следующая

Теорема. Если ранг матрицы Х равен p, то оценки параметров _j некоррелированы тогда и только тогда, когда столбцы матрицы Х попарно ортогональны.

Доказательство. Некоррелированность оценок означает, что при i  j, в этом случае матрица является диагональной.

Попарная ортогональность столбцов матрицы Х означает, что при i  j выполняются равенства

,

а поскольку , это означает, что матрица S диагональна и, следовательно, матрица S^–1 диагональна.

Но равенство (10) показывает, что матрицы и S^–1 одновременно диагональны или нет, откуда и следует требуемое утверждение.

5. Функция отклика. Предположим сначала, что при каждом фиксированном значении вектора контролируемых переменных x  (x₁, x₂, ..., x_k) выходная случайная величина y (отклик) является одномерной.

Определение. Среднее значение выходной переменной y, рассматриваемое как функция от вектора контролируемых переменных, называется одномерной функцией отклика или просто функцией отклика (или целевой функцией).

Обозначив эту функцию через , можно записать

. (11)

Областью определения функции (11) является множество G, состоящее из векторов контролируемых переменных x  (x₁, x₂, ..., x_k), реализация которых возможна в эксперименте. Очевидно, G  ^k. Пространство ^k, состоящее из всех векторов x  (x₁, x₂, ..., x_k) (см. Введение, § 2, п. 6), принято называть факторным пространством.

Множество точек вида (x₁, x₂, ..., x_k, (x₁, x₂, ..., x_k)) называется поверхностью отклика. Другими словами, поверхность отклика есть множество точек (x₁, x₂, ..., x_k, )   ^k+1, удовлетворяющих уравнению   (x₁, x₂, ..., x_k).

Положим , тогда , или просто . Величину называют ошибкой измерения функции отклика и интерпретируют как случайную помеху или шум, содержащийся в выходных данных.

Многомерная функция отклика определяется аналогично. Именно, если отклик y  ( y₁, y₂, ..., y_r) есть r-мерный случайный вектор, то полагаем

η(x)  M(y / x)  (M(y₁ / x), M( y₂/ x), ..., M( y_r / x)),

где через M( y_i / x) обозначено условное математическое ожидание случайной величины y_i при фиксированном значении вектора x.

6. План эксперимента. Одномерная регрессионная модель эксперимента. Рассмотрим – эксперимент, т. е. такой эксперимент, в котором проводится N измерений одномерной зависимой переменной y в некоторых точках x факторного пространства.

Определение 1. Набор точек x_u  (x_1u, x_2u, ..., x_ku) (u  1, 2, ..., N) называется планом эксперимента. Матрица

(12)

называется матрицей плана эксперимента.

Заметим, что точки x_u не обязательно все различны. Обозначим через n число различных точек плана; для определенности будем предполагать, что это точки x₁, x₂, ..., x_n (n m N).

Определение 2. Спектром плана называется совокупность величин x₁, x₂, ..., x_n; m₁, m₂, ..., m_n, где x₁, x₂, ..., x_n – различные точки плана, – число наблюдений в точке x_i .

Эксперимент называют активным, если имеет место выбор плана, и пассивным в противном случае.

В пассивном эксперименте матрица плана предполагается заданной или является предопределенной условиями проведения эксперимента. Задача исследователя состоит в выполнении наблюдений над выходной (зависимой) переменной в точках, определяемых матрицей плана, и последующем анализе результатов. В активном эксперименте задача построения плана является одной из центральных.

В общем случае вид функции отклика неизвестен. Предположим, что она является одномерной и представлена в виде:

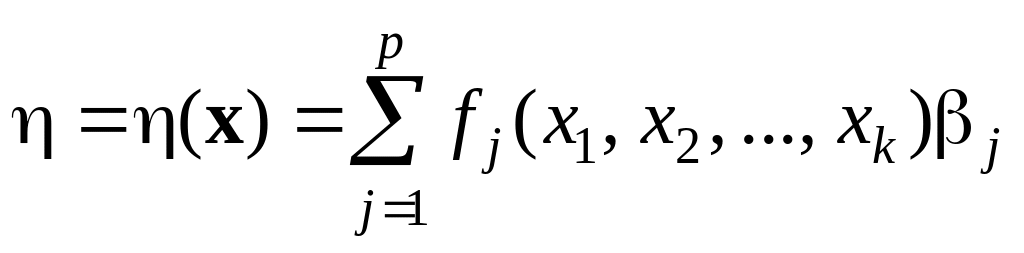, (13)

где _j – неизвестные параметры, а f_j – известные функции.

Функцию отклика такого вида называют регрессионной моделью эксперимента.

Пусть задана матрица плана (12) и в точках плана, определяемых этой матрицей, проводится N наблюдений над зависимой переменной y. Пусть – наблюдение зависимой переменной в точке x_u  (x_1u, x_2u, ..., x_ku), тогда из (11) и (13) следуют при всех u  1, 2, ..., N равенства

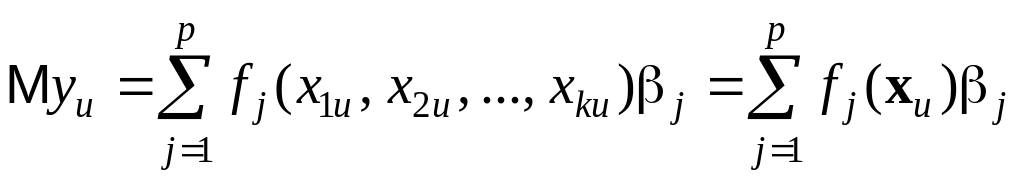. (14)

Определение 3. Матрица

называется матрицей планирования эксперимента с матрицей плана (12) и функцией отклика (13).

Пусть y  ( y₁ y₂ ... y_N)^T – вектор-столбец наблюдений, β  (₁ ₂ ... _p)^T – вектор-столбец неизвестных параметров. Тогда равенства (14) можно записать одним матричным равенством , так что выполняется первое из равенств (3). Далее будет предполагаться, что наблюдения y₁, y₂, ..., y_N некоррелированны и имеют одинаковую дисперсию ², т. е. выполняется и второе равенство (3).

Пример 1. Пусть  (2  4  –3  1)^T – матрица плана, – функция отклика. Тогда f₀(x)  1, f₁(x)  x, f₂(x)  x². Матрица планирования имеет вид

.

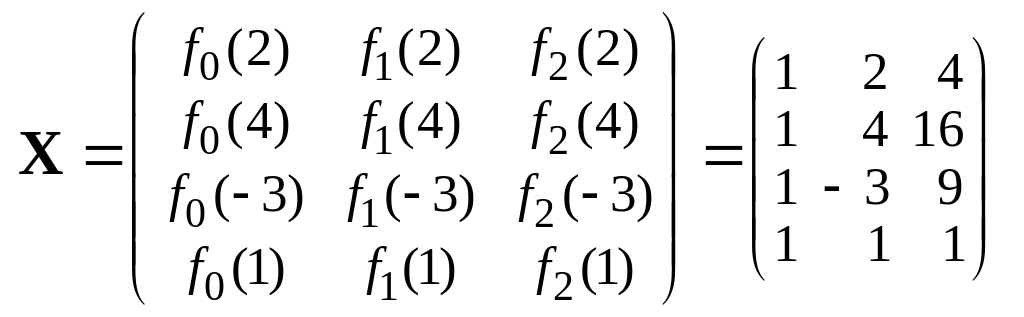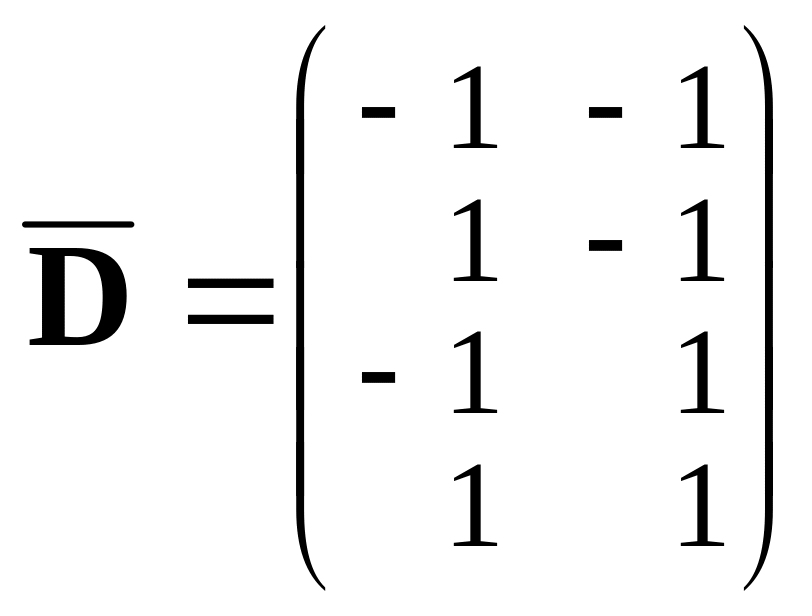Пример 2. Пусть – функция отклика, – матрица плана. Тогда f₁(x)  1, f₂(x)  x₁, f₃(x)  x₂, f₄(x)  x₁x₂; x₁  (–1, –1), x₂  (1, –1), x₃  (–1, 1), x₄  (1, 1). Матрица планирования