§ 4. Однофакторный дисперсионный анализ

1. Постановка задачи. Пусть случайные величины ₁, ₂, ..., _p распределены по нормальному закону и имеют одинаковую и притом неизвестную дисперсию ², математические ожидания также неизвестны, но могут быть различными. Требуется при заданном уровне значимости проверить гипотезу о равенстве всех математических ожиданий: M₁  M₂  ...  M_p. Для этого используется метод, основанный на сравнении некоторых дисперсий и поэтому названный дисперсионным анализом.

На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние определенный качественный фактор F, который имеет p уровней F₁, F₂, ..., F_p на изучаемую величину , которая под воздействием этих факторов превращается соответственно в ₁, ₂, ..., _p.

Например, если требуется выяснить, какой вид цемента наиболее эффективен для получения наибольшей прочности бетона, то фактор F есть цемент, а его уровни – виды цемента.

Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии, порождаемой воздействием фактора, с остаточной дисперсией, обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на изучаемую величину .

В этом случае средние наблюдаемых значений (выборочные математические ожидания) на каждом уровне (групповые средние) различаются также значимо. Если уже установлено, что фактор существенно влияет на величину , и требуется выяснить, какой из уровней оказывает на нее наибольшее воздействие, то дополнительно производят попарно сравнение средних.

Дисперсионный анализ применяют также, чтобы установить однородность нескольких совокупностей, которая понимается в том смысле, что связанные с ними случайные величины при предположенных одинаковых дисперсиях имеют также и одинаковые математические ожидания.

Однородные совокупности можно объединить в одну и тем самым получить о них более полную информацию, а значит, и более надежные выводы.

2. Общая, факторная и остаточная суммы квадратов отклонений. Пусть на количественный признак, значение которого есть нормально распределенная случайная величина, воздействует фактор F, имеющий p постоянных уровней. Пусть проведена группа из q₁ испытаний при уровне F₁, группа из q₂ испытаний при уровне F₂, ..., группа из q_p испытаний при уровне F_p. Обозначив через x_ij значение, полученное в i-м испытании при j-м уровне, имеем следующую таблицу результатов.

i (номер испы- тания)	Уровни фактора
			...
1	x11	x12	...	x1p
2	x21	x22	...	x2p
…	...	...	...	...
q1		…	...	…
...		...	...	...
q2			...	...
...			...	...
qp			...
Груп­повая средняя			...

Пусть , где , т. е. – общее среднее всех x_ij. Введем в рассмотрение суммы:

– общая сумма,

– факторная сумма,

– остаточная сумма.

Общая сумма является суммой квадратов отклонений наблюдаемых значений от общей средней, факторная сумма есть сумма квадратов отклонений групповых средних от общей средней, остаточная сумма представляет собой сумму квадратов отклонений наблюдаемых значений от своей групповой средней.

Теорема. Выполняется равенство S_общ  S_факт + S_ост.

Доказательство. Имеем

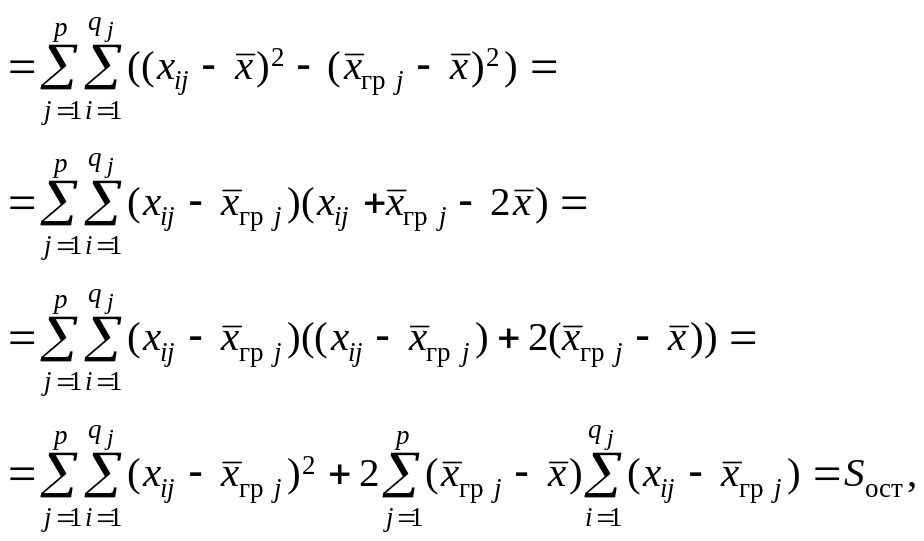
т. к.

Замечание 1. Если фактор F оказывает существенное влияние на значения количественного признака, то группы наблюдаемых значений, соответствующие различным уров­ням, заметно отличаются друг от друга. Следовательно, групповые средние больше отклоняются от общей средней, а чем больше это отклонение, тем больше S_факт. Таким образом, факторная сумма характеризует воздействие фактора на количественный признак. Остаточная сумма S_ост суммирует рассеяния наблюдаемых значений относительно групповых средних и, таким образом, является характеристикой воздействия случайных причин. Следовательно, S_общ  S_факт + S_ост отражает как влияние фактора, так и влияние случайных причин.

Замечание 2. Выражения для общей и факторной сумм можно привести к виду, более удобному для вычислений. Для этого введем обозначения: , .

Используя эти обозначения, получаем

,

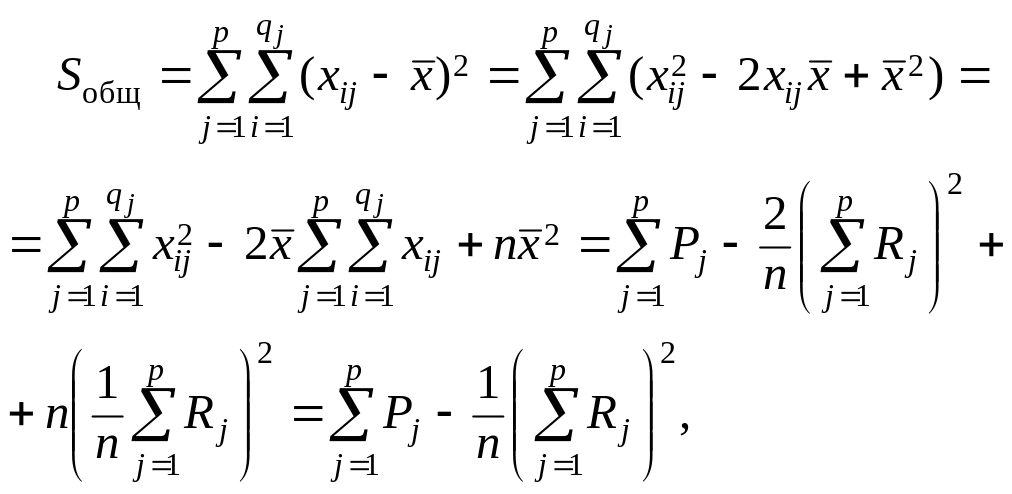
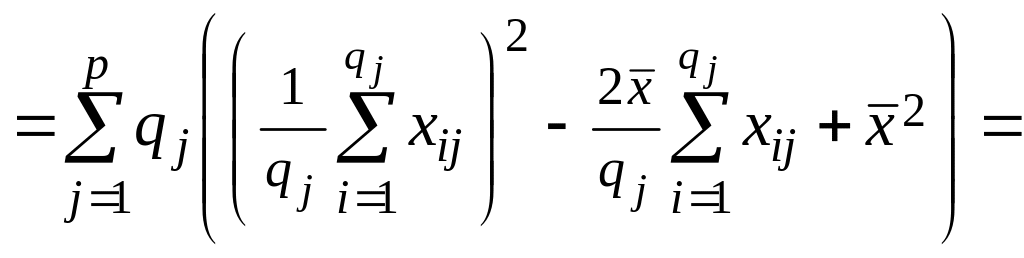
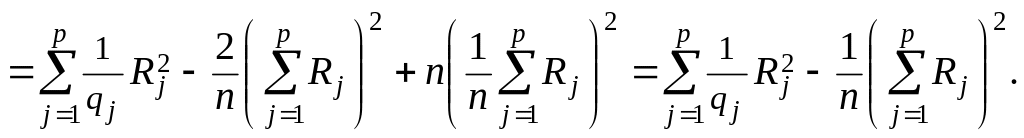
Таким образом, имеют место формулы

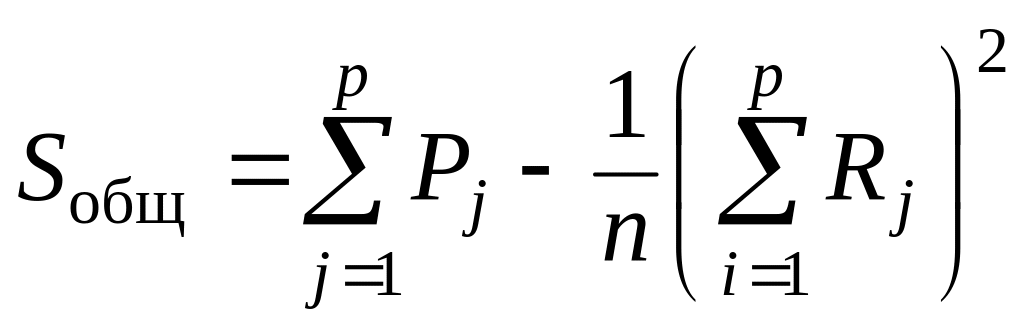и .

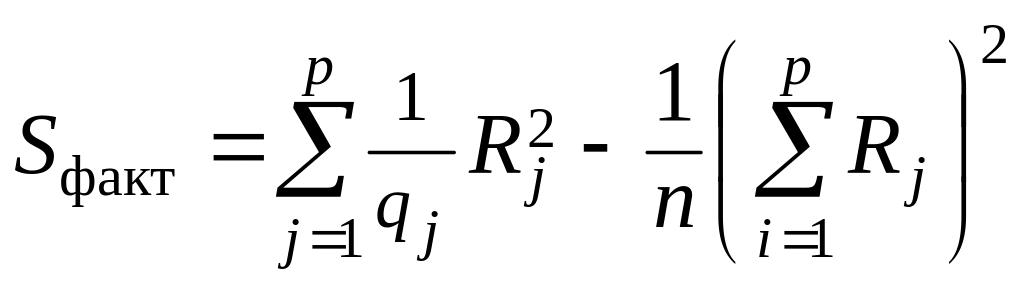3. Общая, факторная и остаточная дисперсии. Введем следующие обозначения:

, , .

Эти величины называют соответственно общей, факторной и остаточной дисперсиями. Так как все x_ij при сделанных в п. 1 предположениях представляют собой независимые случайные величины, распределенные по нормальному закону с дисперсией ², то есть несмещенная точечная оценка для ².

Предположим, что верна гипотеза , т. е. M₁  M₂   ...  M_p  a. Тогда и все групповые средние являются несмещенными точечными оценками одного и того же числа а. Поэтому при любом j есть также несмещенная точечная оценка для ², так что , а следовательно,

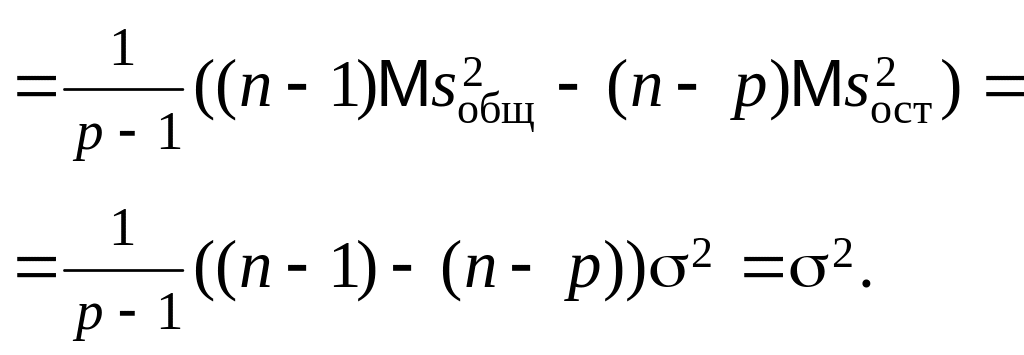
Таким образом, если гипотеза верна, то и являются несмещенными точечными оценками для дисперсии ². Можно доказать, что эти оценки являются независимыми случайными величинами. Поэтому при построении критерия для проверки гипотезы используются именно эти оценки.

4. Сравнение нескольких математических ожиданий методом дисперсионного анализа. Пусть случайные величины , ,..., распределены по нормальному закону и имеют одинаковую неизвестную дисперсию ², математические ожидания также неизвестны, но могут быть различными. Построим критерий для проверки при заданном уровне значимости гипотезы : M₁  M₂  ...  M_p .

Если эта гипотеза верна, то при любом j есть исправленная выборочная дисперсия для _j (см. п. 3), а тогда (§ 2, п. 3 (в)) случайная величина распределена по закону ^ с q_j – 1 степенями свободы. Отсюда следует, что случайная величина распределена по закону ^ с q₁ + q₂ + ... + q_p – p  n – p степенями свободы. Таким же образом получаем, что случайная величина распределена по закону ^ с числом степеней свободы n – 1. Отсюда следует, что разность распределена по закону ^ с (n – 1) – (n – p)  p – 1 степенями свободы. Значит, случайная величина

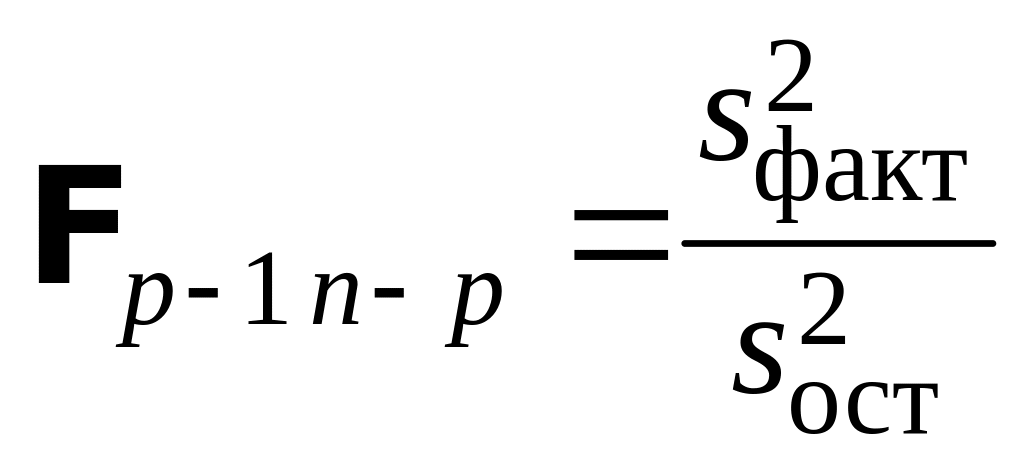
распределена (при условии справедливости гипотезы H₀) по закону Фишера со степенями свободы p – 1 и n – p. Эта случайная величина и является критерием для рассматриваемой гипотезы.

Решение задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера.

Действительно, если верна гипотеза , то факторная и остаточная дисперсии являются несмещенными оценками неизвестной дисперсии (см. п. 3) и, значит, различаются незначимо. Если же гипотеза о равенстве групповых математических ожиданий неверна, то с возрастанием расхождения между групповыми средними возрастает факторная дисперсия, а тогда возрастает и . В конце концов, F_набл окажется больше F_кр и, значит, гипотеза о равенстве групповых математических ожиданий должна быть отвергнута. Если же окажется F_набл< F_кр, гипотеза принимается.

Если факторная дисперсия окажется меньше остаточной, то отсюда сразу следует справедливость гипотезы о равенстве групповых математических ожиданий, т. е. нет необходимости применять критерий Фишера.

Пример. Пусть произведено 14 испытаний на различных уровнях фактора F: 5 испытаний на уровне F₁, 3 испытания на уровне F₂, 2 испытания на уровне F₃ и 4 испытания на уровне F₄. Результаты испытаний представлены следующей таблицей.

i (номер ис- пытания)	Уровни фактора
			F3	F4
1	1,5	3,3	5,6	6,1
2	2,1	3,1	4,8	5,9
3	1,4	4,5		4,7
4	2,2			4,3
5	2,4

Требуется проверить на уровне значимости   0,05 гипотезу о равенстве математических ожиданий нормально распределенных случайных величин ₁, ₂, ₃, ₄, возникающих при различных уровнях фактора F. Предполагается, что дисперсии этих случайных величин одинаковы. Обозначим через x_ij значение, полученное в i-м испытании при j-м уровне фактора, и составим расчетную таблицу.

i
1	1,5	3,3	5,6	6,1	2,25	10,89	31,36	37,21
2	2,1	3,1	4,8	5,9	4,41	9,61	23,04	34,81
3	1,4	4,5		4,7	1,96	20,25		22,09
4	2,2			4,3	4,84			18,49
5	2,4				5,76
Rj	9,6	10,9	10,4	21,0
Pj					19,22	40,75	54,40	112,60
	92,16	118,81	108,16	441

Отсюда ;

; .

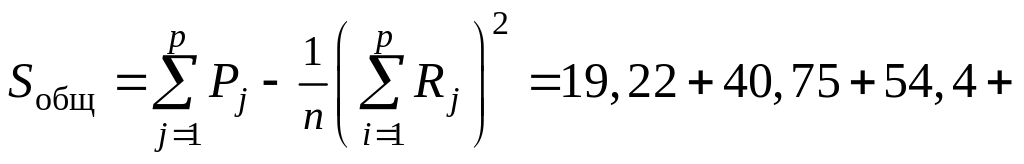
Далее найдем факторную и остаточную дисперсии: ; .

Получаем F_набл = . По таблице критических точек распределения Фишера находим F_кр = 3,71. Так как F_набл > F_кр, гипотеза отвергается.