§ 2. Доверительные интервалы для параметров функции отклика и гипотеза адекватности

1. Дополнительные сведения из дисперсионного анализа. В этом параграфе будет предполагаться, что наблюдения y_is (i  1, 2, ..., n; s  1, 2, ..., m_i) нормально распределены и при этом выполняются условия:

; , (1)

где , 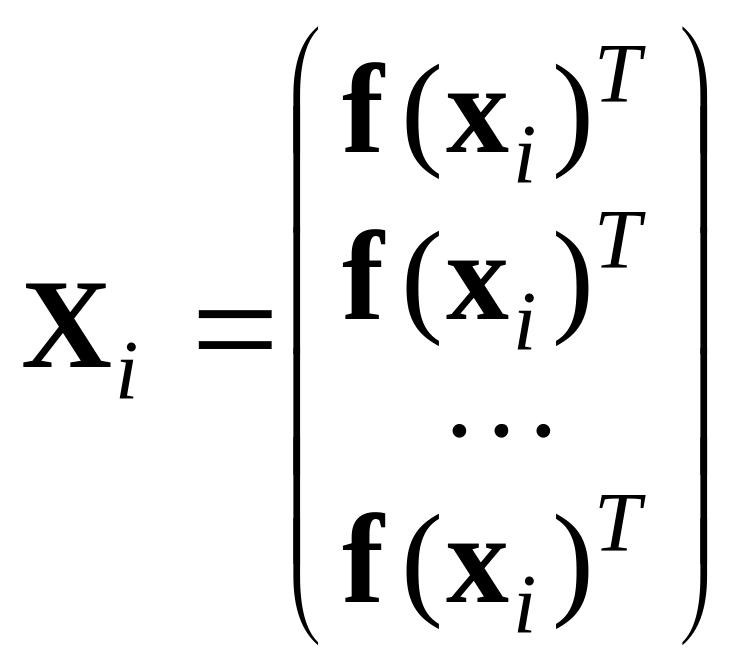– матрица размера с одинаковыми строками (i 1, 2, ..., n), β  (₁ ₂ ... _p)^T и .

Из первого уравнения (1) получаем при всех i  1, 2, ..., n где обозначено . Следовательно, имеем

(i  1, 2, ..., n; s  1, 2, ..., m_l).

Положим , ( – произвольный вектор-столбец размерности p). Возведем в квадрат обе части тождества и просуммируем по s и по i. Получим

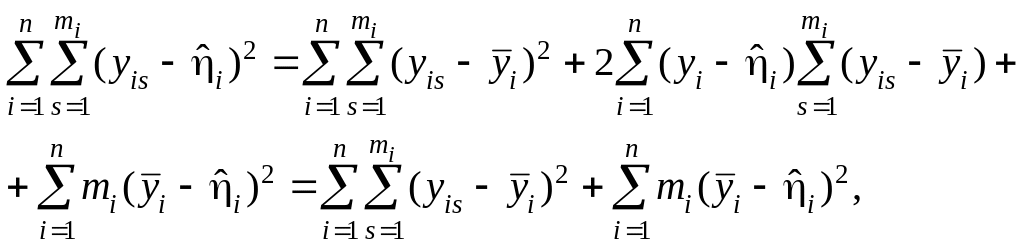
поскольку (i  1, 2, ..., n). Таким образом, имеем равенство

S₀  S₁ + S₂, (2)

где обозначено , , . Предположим теперь, что эти суммы получены при условии, что – МНК-оценка вектора β параметров функции отклика, найденная в п. 8 § 1, и введем в рассмотрение следующие величины

, , .

Можно доказать, что при сделанных предположениях эти величины обладают свойствами, аналогичными свойствам величин , и , установленным в пунктах 3 и 4 § 4 гл. 1. Именно, все они являются несмещенными оценками дисперсии ² и при этом случайные величины

, и

распределены по закону с числами степеней свободы соответственно N – p, n – p и N – n, причем две последние из них являются независимыми.

2. Доверительные интервалы для параметров функции отклика. Напомним (см. гл. 1, § 2, п. 1), что доверительным интервалом называют интервал, который с заданной надежностью  покрывает оцениваемый параметр.

Пусть – вектор-столбец МНК-оценок параметров функции отклика. Поскольку , где y – случайный вектор с независимыми компонентами, распределенными по нормальному закону, то все также распределены по нормальному закону. Так как МНК-оцен­ки являются несмещенными (см. § 1, п. 3), имеем ( j  1, 2, ..., p). Кроме того, равенство (10) из п. 4 § 1 показывает, что , где – элемент матрицы . Значит, случайная величина

распределена по нормальному закону c параметрами M  0 и D  1. Обозначим также

,

где сумма S₀ построена по оценкам так же, как в п. 1. Поскольку эта случайная величина распределена по закону χ² с числом степеней свободы N – p, случайная величина

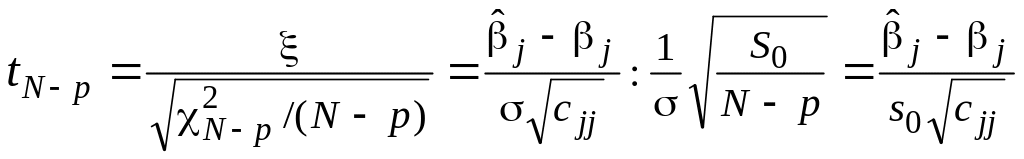(3)

распределена по закону Стьюдента с N – p степенями свободы.

При заданном  (0 <  < 1) по таблице для распределения Стьюдента можно найти число t_, удовлетворяющее уравнению P(| t_N-p t_, так что с вероятностью  будем иметь , или, что равносильно,

,

откуда следует что – доверительный интервал для параметра с надежностью .

Замечание. Случайная величина (3) может быть использована для проверки гипотезы H₀ о том, что некоторый параметр функции отклика равен 0. Действительно, если эта гипотеза верна, то получаем

,

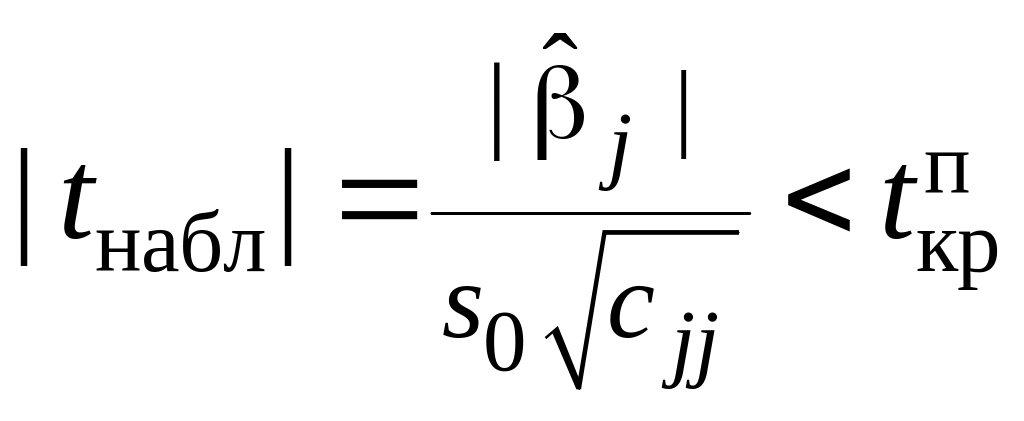причем эта случайная величина должна распределяться по закону Стьюдента с N – p степенями свободы. При альтернативной гипотезе H_A: критическая область является двусторонней. Найдем для заданного уровня значимости  и числа степеней свободы N – p по таблице 4 правую критическую точку . Тогда имеем следующие возможности: , в этом случае нет оснований отвергать гипотезу H₀; если же , то гипотеза H₀ отвергается.

3. Проверка гипотезы адекватности модели. Пусть определенная в области G функция отклика

неизвестна, т. е. неизвестны функции и параметры _j, и задан спектр плана: ; , где . Если – повторные наблюдения в точке x_i (i  1, 2, ..., n), то матрица плана имеет вид 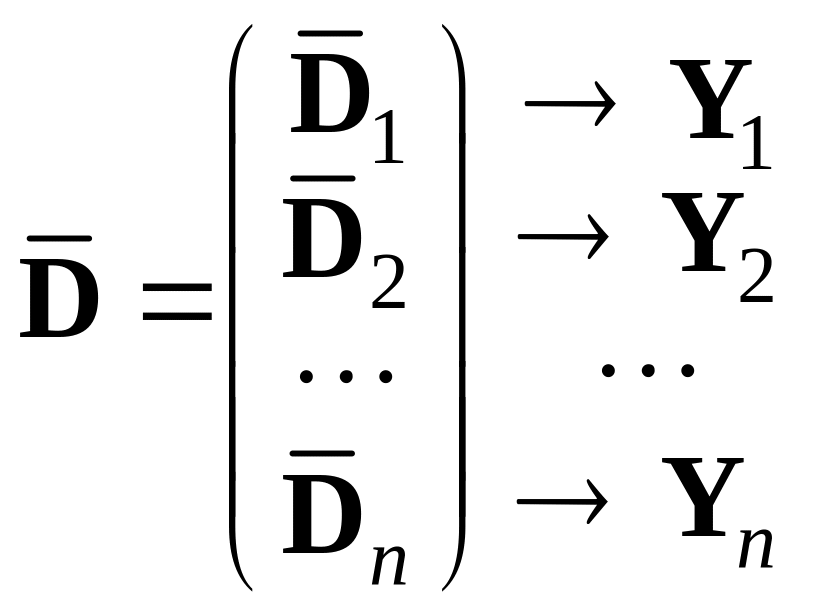, где – матрица размера , строки которой одинаковы, и – вектор-столбец наблюдений в точке x_i, соответствующий матрице (это соответствие показано стрелками).

Положим

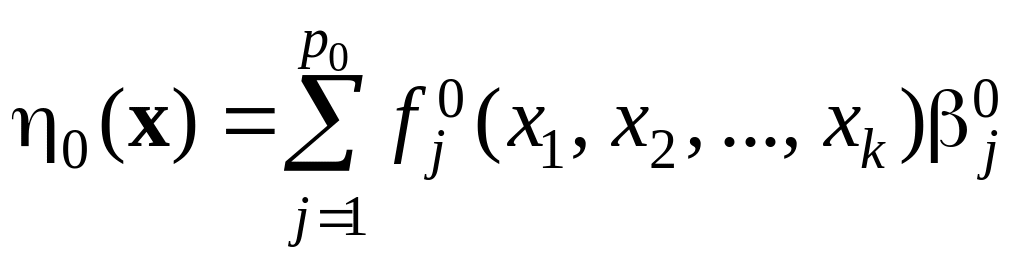, (4)

где – заданные функции.

Гипотезу H₀ о том, что при всех xG выполняется равенство , называют гипотезой адекватности регрессионной модели или функции отклика (4). Она проверяется при альтернативной гипотезе H_А: .

Если гипотеза H₀ верна, то МНК-оценка функции отклика равна

.

Пусть и (i  1, 2, ..., n). Рассмотрим суммы

,

, где .

Как доказано в п. 1, для таких сумм имеет место равенство (2). Заметим также, что сумма S₁ должна, очевидно, быть небольшой, если модель адекватна, так что ее величина является характеристикой степени адекватности; сумма S₂ связана с дисперсией ошибок наблюдения, поэтому ее называют ошибкой эксперимента. Обозначим

, .

Если гипотеза H₀ верна, то эти величины совпадают соответственно с величинами и , рассмотренными в п. 1, значит, случайные величины

и

независимы и распределены по закону с числами степеней свободы соответственно и N – n. Отсюда следует, что если основная гипотеза верна, то случайная величина

имеет распределение Фишера с и N – n степенями свободы.

Вычислив и найдя по таблице распределения Фишера по уровню значимости  и степеням свободы n – p₀ и N – n , получаем следующие возможности:

, в этом случае нет оснований отвергать основную гипотезу;

, тогда основную гипотезу отвергаем.

Если гипотеза H₀ отвергается, модель (4) считается неадекватной и приходится выбирать другую модель. Выбор новой модели зависит от характера задачи, стоящей перед исследователем. Может возникнуть необходимость в проведении дополнительных наблюдений для проверки новой гипотезы.