0. Подавление помех активными фильтрами.

Нормализация сигналов

Эффективным способом подавления продольных помех, как было показано выше, является применение дифференциальных схем подавления синфазных помех и применение гальванических развязок. Одним из эффективных способов подавления поперечных помех (если спектры мощности помех и сигналов не совпадают) является фильтрация сигналов.

Для оценки степени «засоренности» полезного сигнала помехами используют понятие отношения сигнал-шум (с/ш). Оно определяется по формуле

К_сш=U /U (8.9)

где U - квадрат амплитуды среднего полезного сигнала, U - квадрат амплитуды среднего сигнала помехи.

Через это отношение удобно, например, выразить степень улучшения качества сигнала дифференциальным усилителем с высоким коэффициентом ослабления синфазного сигнала. Если отношение с/ш на входе усилителя обозначить как К_сшвх, то на выходе это соотношение будет определяться формулой

К_сшвых=К_сшвх*К , (8.10)

где К_осс= - коэффициент ослабления синфазного сигнала; К_пс - коэффициент передачи полезного сигнала; К_псс – коэффициент передачи синфазного сигнала помехи.

В общем случае, как полезный сигнал, так и сигнал помехи можно считать случайными функциями времени, свойства которых задаются вероятностями характеристиками. Часто известны бывают две из них: интенсивность сигнала (задаваемая либо среднеквадратичным значением, либо среднеквадратичной плотностью) и граничная частота спектра сигнала ω_гр, определяемая полосой частот, в которой сосредоточена большая часть мощности сигнала.

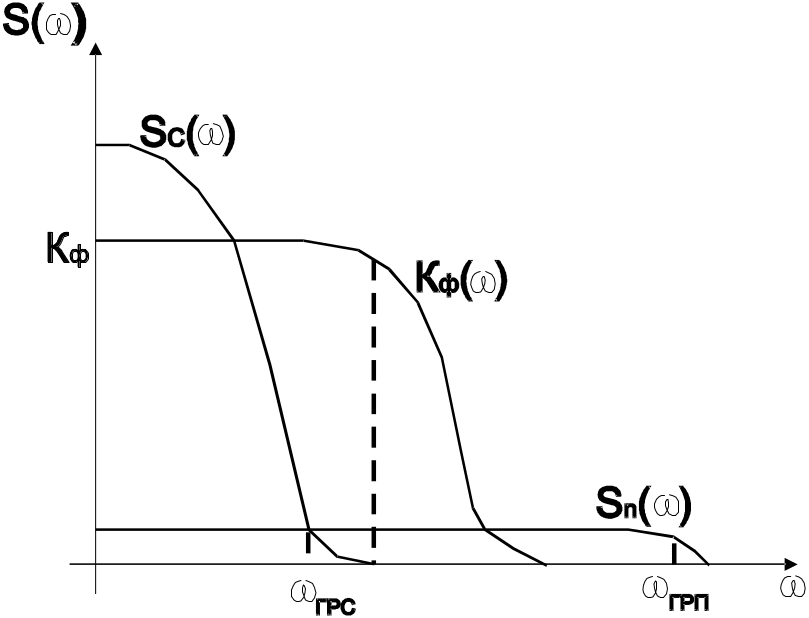
Рисунок 8.11

На рис.8.11 показан пример спектрального состава полезного S_с(ω) и шумового S_П(ω) сигналов с граничными частотами спектра ω_грс и ω_грп соответственно.

Если на выходе устройства, несущего полезный сигнал и сигнал помеху, поставить фильтр нижних частот с частотной характеристикой К_ф(ω), которая согласована со спектром полезного сигнала (пропускает без подавления полезный сигнал), то для этого примера нетрудно видеть, что значительная часть сигнала помехи будет подавлена.

Отношение с/ш на выходе фильтра можно оценить по приближенной формуле

К_сшф 0,5К_сшу(ω_грп/ω_ср), (8.11)

где К_сшу – отношение сигнал/шум на выходе усилителя, после которого осуществляется фильтрация.

Если обеспечить реализацию комплексного подавления помехи (нормализация сигнала) с помощью схемы синфазного подавления и с помощью схемы фильтрации, то совместная запись выражений 8.10 и 8.11 позволяет получить соотношение

К_сшу=К_сшвых,

К_сшф/К_сшвх=0,5(ω_грп/ω_ср)К . (8.12)

Формула 8.12 позволяет оценить общее повышение соотношения с/ш схемой нормализации.

При оценке реально достижимого отношения с/ш для рассматриваемого случая, необходимо учитывать несколько взаимно-противоречивых факторов. Понижение частоты среза фильтра низких частот (ФНЧ) приводит к улучшению подавления помех, но нельзя ω_ср выбирать ниже граничной частоты спектра полезного сигнала, чтобы не исказить полезную информацию.

С другой стороны, любой ФНЧ – это инерционная динамическая система, и с понижением ω_ср ее инерционность растет. Эти соображения необходимо учитывать при реализации любых фильтров.

Кроме того, улучшая качество сигнала, необходимо учитывать, что нет смысла «давить» шумы существенно ниже, чем погрешность используемых датчиков.