Лінія ринку цінних паперів (security market line, sml)

Лінійність ефективної множини за наявності безризикового активу дала змогу розвинути сучасну портфельну теорію і привела до появи моделі оцінки дохідності активів CAPM. Модель CAPM дозволяє інвесторам оцінити альтернативи «ризик – дохідність», використовуючи коефіцієнт і ринкову дохідність для визначення очікуваної дохідності цінних паперів. Модель представлена таким рівнянням:

5.2.16

де - очікувана дохідність цінного папера за даного рівня ризику, що вимірюється за допомогою коефіцієнта ; - дохідність безризикового активу; - коефіцієнт цінного папера; - ринкова дохідність (середня дохідність усіх цінних паперів інвестиційного ринку).

Коефіцієнт - це показник недиверсифікованого, (ринкового) ризику, котрий відображає, як актив інвестиційного портфеля реагує на ринкові сили. Визначається через аналіз взаємозв’язку фактичної дохідності активу з фактичною ринковою дохідністю. Чим вище , тим вищий ризик активу інвестиційного портфеля.

У розрахунках коефіцієнта використовується показник дохідності ринкового портфеля. Ринкова дохідність інвестиційного портфеля вимірюється як середній показник дохідності всіх його інструментів (цінних паперів, активів).

Коефіцієнт обчислюється окремо для кожного активу, що входить до складу інвестиційного портфеля, і дорівнює відношенню коваріації дохідності активу, що розглядається, і дохідності ринку в цілому, чи ринкового індексу (позначеної тут через ) до дисперсії дохідності ринку (позначеної через ). Коефіцієнт для цінного папера х подається співвідношенням:

5.2.17

Для інвестиційного портфеля в цілому коефіцієнт дорівнює :

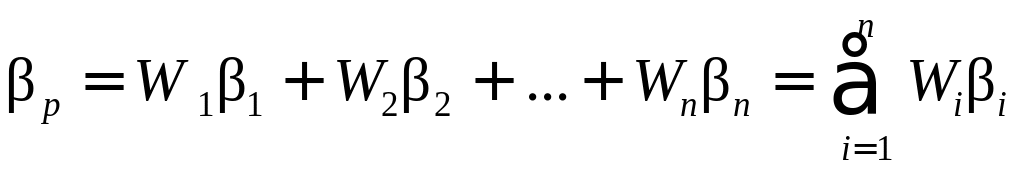5.2.18

де - -коефіцієнт інвестиційного портфеля, який характеризується нестійкістю портфеля цінних паперів порівняно з ринковим; - частка активу і в інвестиційному портфелі; - коефіцієнти для окремих інструментів інвестиційного портфеля ( -коефіцієнт активів і).

Отже -коефіцієнт інвестиційного портфеля є середньою питомою величиною « » усіх окремих цінних паперів, які містяться у ньому. Існують такі види коефіцієнта : «іcторична »; «ринкова »; «скоригована »; «галузева »; «фундаментальна ».

«Історична (статистична) » - міра статистичної коваріації цінного папера і ринкового диверсифікованого портфеля, яка розраховується як відношення коваріації цінного папера до дисперсії інвестиційного портфеля. Взагалі «історичну » можна визначити як нахил графіка ринкової моделі. Якщо цей коефіцієнт був побудований від дати до дати, то «історичну » можна оцінити через зіставлення минулих даних дохідності цінного папера, що розглядається, і дохідності інвестиційного ринку. Статистична процедура для отримання таких апостеріорних значень коефіцієнта називається простою лінійною регресією. Отже, «історичну » слід визначити як оцінку -коефіцієнта цінного папера інвестиційного портфеля, яка випливає із статистичних, даних про його дохідність (див. фор. 5.2.17) .

Найважливіші характеристики киофіцієнта :

1) вимірю не диверсифікований (ринковий) ризик, пов’язаний з цінним папером ін вест. портфеля;

2) для ринку в цілому дорівнює 1;

3) цінні папери можуть мати як додатне, так і від’ємне значення , але більшість з них додатні;

4) цінні папери ін вест. портфеля, у яких > 1, чутливі до зміни ринкової дохідності (більш ризиковані ніж ринок в цілому); якщо < 1, менш ризикові ніж ринок;

5) чим вища , тим вищій рівень очікуваної доідності фінансового інструменту, і навпаки.

Модель В. Шарпа - CAPM може також бути зображена графічно у вигляді лінії ринку цінних паперів – SML ( «характеристичної лінії ринку» чи «лінії дохідності ринку цінних паперів»).

Лінію ринку цінних паперів SML можна визначити як лінію на графіку, що показує співвідношення між ризиком, визначеним за допомогою - коефіцієнта, і потрібною ставкою дохідності для окремих цінних паперів інвестиційного портфеля (рис 5.2.3.)

Лінія ринку цінних паперів є прямою. Її можна побудувати, вирахувавши потрібну (очікувану) дохідність для різноманітних значень фактора β, залишаючи ставку дохідності безризикових активів і ринкову дохідність постійними, використовуючи при цьому рівняння САРМ.

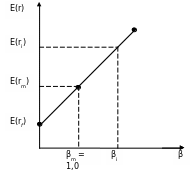
Рис. 5.2.3. Лінія ринку цінних паперів SML

У графічному зображенні SML «очікувана дохідність – коефіцієнт β» ціні папери, на які встановлено справедливі ціни, розташовані на лінії SML. Цінні папери ж, ціни яких завищені, перебувають вище SML (тобто при однакових значеннях β їх очікувані ставки дохідності розташовані вище значень, вказаних САРМ). Цінні папери ж, цни котрих занижені, перебувають нижче SML.

Різниця між справедливими і фактичними очікуваними ставками дохідності цінних паперів називається коефіцієнтом α (альфа). Отже, коефіцієнт α розраховується як різниця між очікуваною дохідністю цінного папера і його рівноважною (очікуваною) дохідністю, і використовується для вибору серед однакових за ризиком ціних паперів таких, які мають вищу дохідність.

Приклад 5.2.1.

Знайдіть очікувану дохідність цінних паперів «А» та «Б» за допомогою моделі В. Шарпа (CAPM), якщо ставка безризикового активу становить 5 % ринкова дохідність (середня дохідність цінних паперів інвестиційного ринку) 9 %, коефіцієнт цінного папера «А» 1,2; а цінного папера «Б» 1,3. Зробіть відповідні висновки.

Розв’язок:

Використовуючи формулу (5.2.16), знайдемо очікувану дохідність для:

цінного папера «А»: = 5 + [1,2 (9 – 5)] = 5 + 4,8 = 9,8 %;

цінного папера «Б»: = 5 + [1,3 (9 – 5)] = 5 +5,2 = 10,2 %.

З отриманих результатів можна зробити висновок про те, що модель CAPM відображає прямі функціональні зв’язки між ризиком і дохідністю цінного папера, оскільки чим вищий ризик , тим вищою буде очікувана дохідність.

Статистичні показники моделі CAPM розраховуються методом найменших квадратів :

: 5.2.19

Коефіцієнт : 5.2.20

Аналіз ефективності управління інвестиційним портфелем банку

У сучасній портфельній теорії існує низка коефіцієнтів, що визначають ефективність управління інвестиційним портфелем банку. Для аналізу ефективності диверсифікованого портфеля зарубіжні економісти, які дотримуються нетрадиційної портфельної теорії, використовують поряд з іншими, коефіцієнт Д. Трейнора (kT), В. Шарпа (kS).

Коефіцієнт Трейнора (kТ) показує середній рівень надлишкової (додаткової) дохідності портфеля на одиницю ризику, враховуючи при цьому системний ризик.

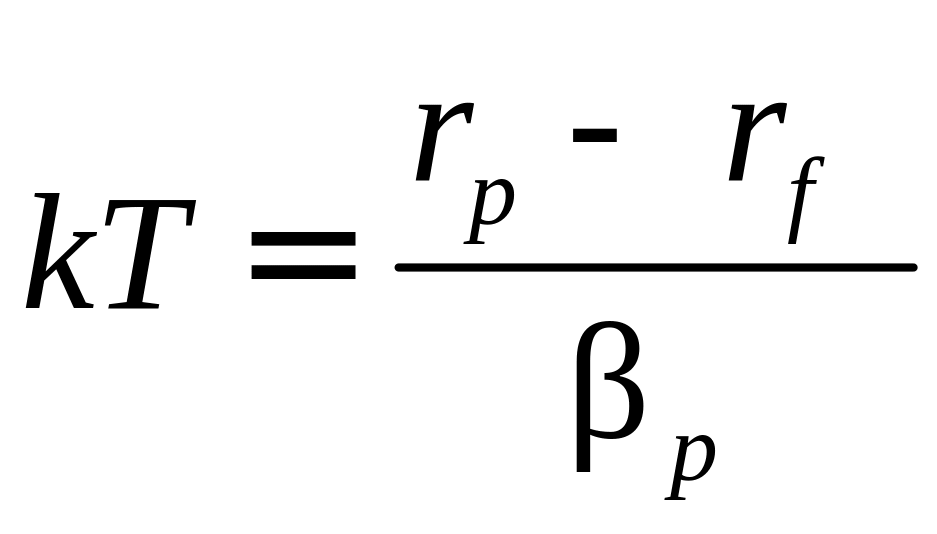5.2.21

де - середня ставка дохідності гіпотетичного інвестиційного портфеля за період, що аналізується; - середня безризикова ставка за той самий період; - рівень системного ризику, який визначається інвестиційного портфеля за період, що аналізується.

Коефіцієнт Шарпа (Ks) обчислюється так :середня додаткова дохідність інвестиційного портфеля ділиться на його стандартне відхилення :

5.2.22

Отже, коефіцієнт Шарпа через стандартне відхилення дає змогу враховувати як системний, так і несистемний ризики, властиві певному портфелю.

Приклад 5.2.2.

Середнє значення дохідності інвестиційного портфеля банку «АБВ» становить -2,35, ринкового інвестиційного індексу: -1,77. Дисперсія (варіація) інвестиційного портфеля банку «АБВ» дорівнює 16,26; а ринкового інвестиційного індексу: 4,37. Коваріація дорівнює 7,27. Знайти іс­торичну та історичну α інвестиційного портфеля банку «АБВ».

Розв 'язання:

Історична інвестиційного портфеля банку «АБВ» (формула 5.2. 17): β = 7,27/4,37 =1,66. Історична α інвестиційного портфеля банку «АБВ» (формула 5. 2. 20): α = (-2,35)-1,66(-1,77) = 0,59.

Стандартне відхилення:

Коефіцієнт корелції

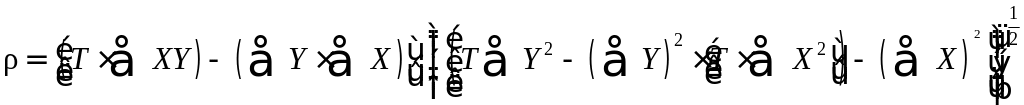
Коефіцієнт детермінації:

Т – кількість періодів (спостережень)

Метою нетрадиційної портфельної теорії є розроблення методів, за допомогою яких інвестор може вибрати оптимальний для себе портфель з нескінченного числа можливих. Для вирі­шення питання про включення кожного розглянутого цінного па­пера в портфель інвестору треба оцінити його очікувану дохід­ність і стандартне відхилення разом з усіма коваріаціями між цими цінними паперами. Використовуючи такі оцінки, інвестор може визначити криву ефективної множини Марковіца. Після цього для даної безризикової ставки треба знайти «дотичний» портфель і визначити положення лінійної ефективної множини. І нарешті, інвестор повинен (сформувати цей «дотичний» порт­фель, визначивши до нього відповідні цінні папери. При цьому сума цінних паперів залежить від переваг інвестора щодо спів­відношення ризику і дохідності.

Приклад 5.2.3.

Середнє значення дохідності інвестиційного портфеля банку «АБВ» становить 29,71; інвестиційного ринку 25,43. Стандартне відхилення інвестиційного портфеля банку «АБВ» 5,76; інвестиційного ринку 4,25, коефіцієнт 1,32; коефіцієнт (-3,77); ставка безризикового активу 6,47. Знайдіть коефіцієнти Трейнора та Шарпа для інвести­ційного портфеля банку «АБВ» та для інвестиційного ринку.

Розв 'язання:

Використовуючи формулу (5.2.21), знайдемо коефіцієнти Трейнора:

для інвестиційного портфеля банку «АБВ»: kТ = (29,71 - 6,47) /1,32 = 17,61;

для інвестиційного ринку: k Т = (25,43 -6,47)/1 = 18,96.

Використовуючи формулу (5. 2.22), знайдемо коефіцієнти Шарпа:

для інвестиційного портфеля банку «АБВ»: kS= (29,71 - 6,47) / 5,76 = 4,03;

для інвестиційного ринку: kS = (25,43 - 6,47) / 4,25 = 4,46.