8. Двумерные случайные величины
Вектор
,
координаты которого есть случайные
величины, заданные на одном и том же
вероятностном пространстве, называется
случайным
вектором, а
функция
называется функцией распределения
случайного вектора
или двумерной случайной величины
.
Если координаты вектора – дискретные случайные величины, то называют дискретным случайным вектором.
Если функцию
распределения вероятности вектора
можно представить в виде
,
то случайную величину
называют непрерывной
двумерной случайной величиной,
а
– ее плотностью
распределения вероятности.
Всюду в дальнейшем будем считать, что – непрерывная функция по обоим аргументам.
Свойства функции и плотности распределения вероятности
1)
.
2)
.
3)
0.
4)
.
5)
, 
,
где
и
– функции распределения случайных
величин
и
.
6)
.
7)
.
8)
.
9)
.
10)
,
,
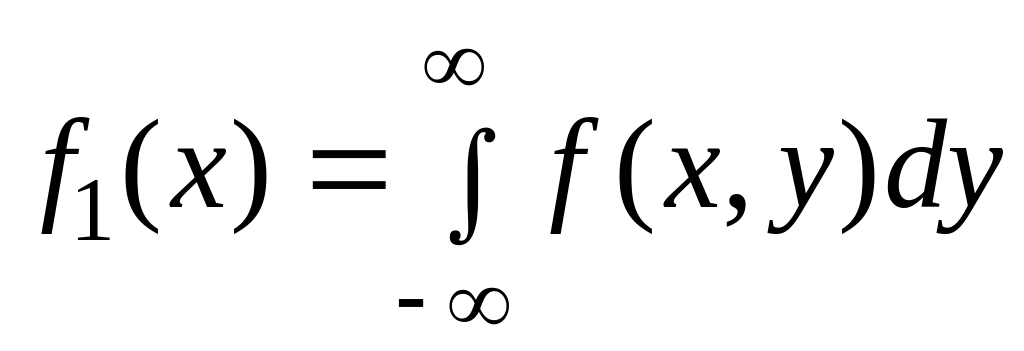где
и
– плотности распределения случайных
величин
и
.
Условной плотностью
распределения случайной величины
при условии
называют предел
,
если он существует.
Аналогично определяют
.
Теорема умножения плотностей
.
Случайные величины
и
называются независимыми,
если для любых чисел
,
случайные события
и
независимы.
Случайные события независимы, если выполняется любое из условий:
1)
2)
.
3)
или
.
Условным математическим ожиданием называют выражение
для дискретного
случайного вектора
для непрерывного
случайного вектора.
Величина
называется корреляционным
моментом (ковариацией)
двух случайных величин
и
.
Если
– непрерывная двумерная случайная
величина с плотностью распределения
,
то
,
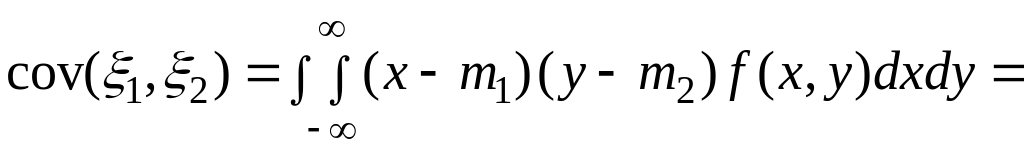
где
.
Для дискретного случайного вектора
.
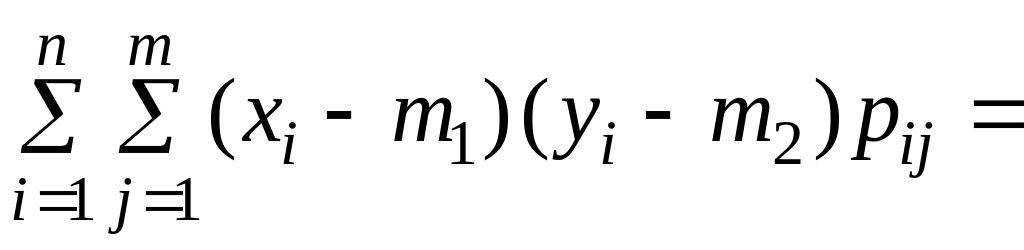
Величина
называется коэффициентом корреляции
случайных величин
и
.
Если
,
то случайные величины
и
называются некоррелированными.
Свойства корреляционного момента и коэффициента корреляции
1)
.
2) Если
и
независимы, то
.
Обратное неверно: из некоррелируемости
случайных величин не следует их
независимость.
3) Если
,
то
4)
.
5)
.
6)
.
7)
.
Свойства математического ожидания и дисперсии
1)
,
где
– постоянная.
2)
.
3)
.
4)
.
Если
,
то
.
Случайная величина
называется неотрицательной
,
если она принимает только неотрицательные
значения.
5) Если
,
.
6)
,
где
– постоянная.
7)
.
8)
.
Если
,
то
.
9)
.
– постоянная.
10)
.
11)
.
Двумерная случайная
величина
называется распределенной
по нормальному закону,
если ее плотность распределения
.
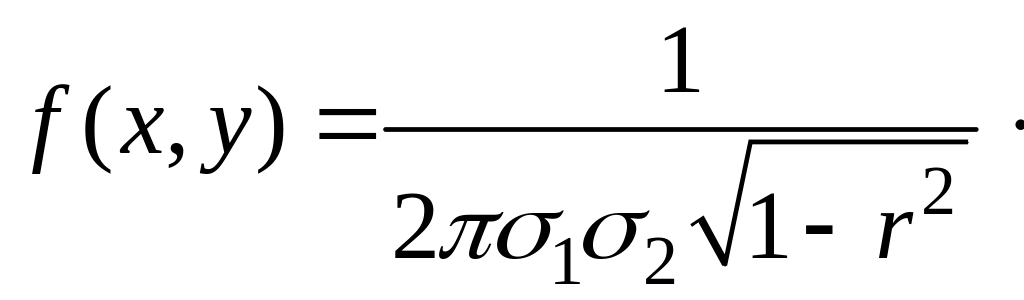
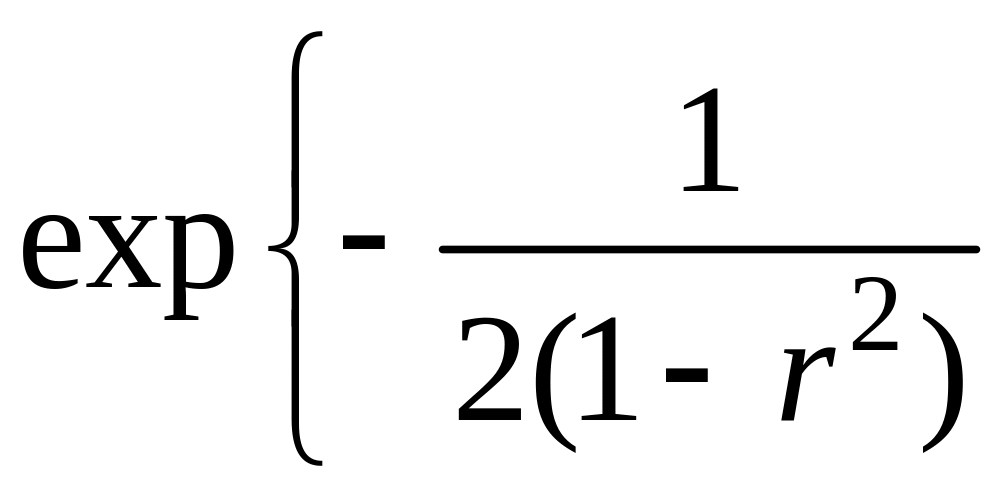
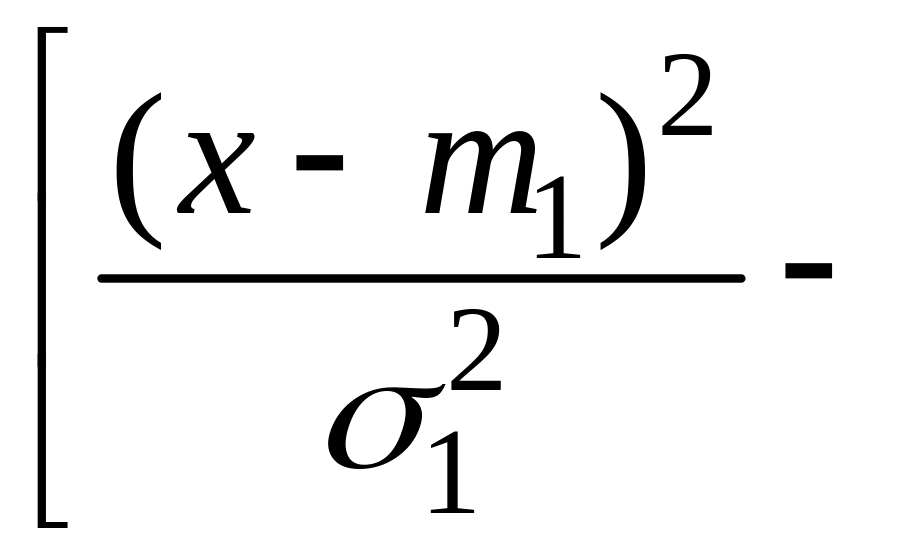
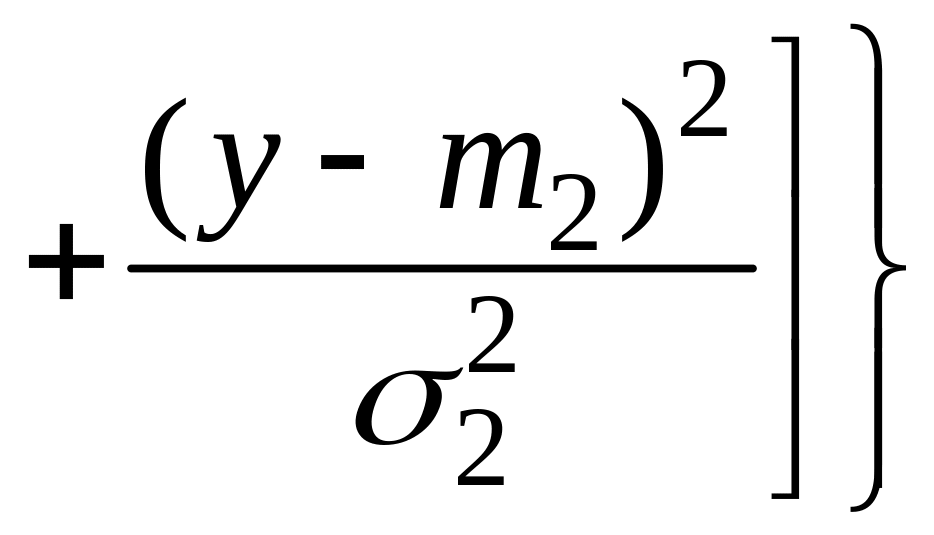Здесь
,
,
,
,
–коэффициент
корреляции случайных величин
и
.
Для нормальной случайной величины
понятия независимости и некоррелируемости
эквивалентны.
Двумерная случайная величина распределена равномерно в области , если ее плотность распределения
Здесь
–
площадь области
.
Пример 1.
Двумерная
случайная величина
имеет равномерное распределение
вероятностей в треугольной области
,
то есть
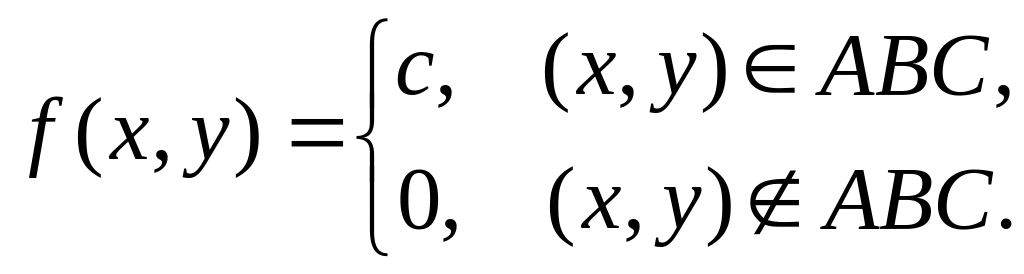
Найти постоянную
,
одномерные плотности
,
случайных величин
и
,
коэффициент корреляции
,
условную плотность
и условное математическое ожидание
.
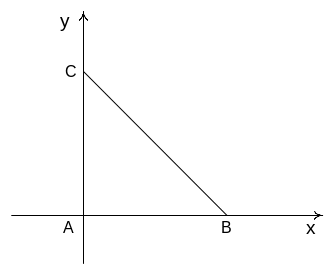
Рис. 2
т.
,
т.
,
т.
.
1) Постоянную найдем из условия нормировки
,
,
где – площадь треугольника . Обозначим область, ограниченную треугольником через . Тогда
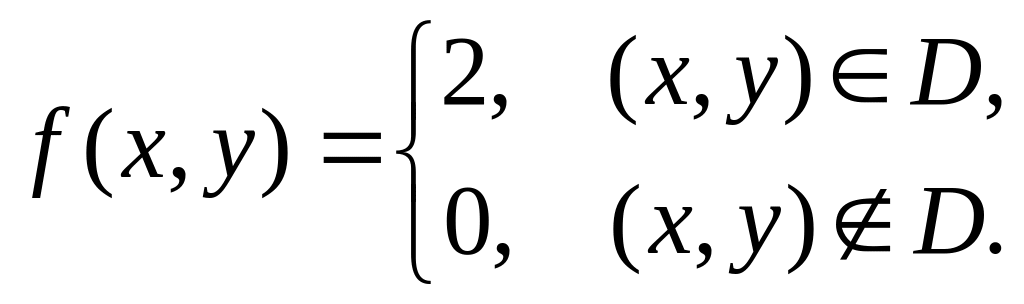
2) Уравнение прямой
.
Тогда область
можно задать аналитически следующим
образом:
или
.
3)
.
.
.
.
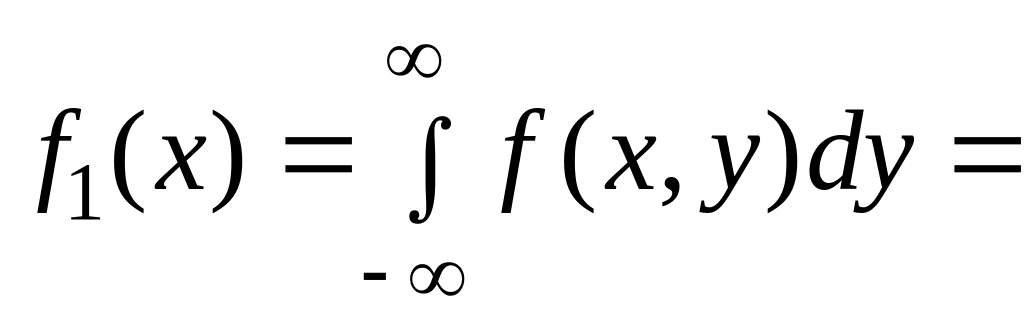
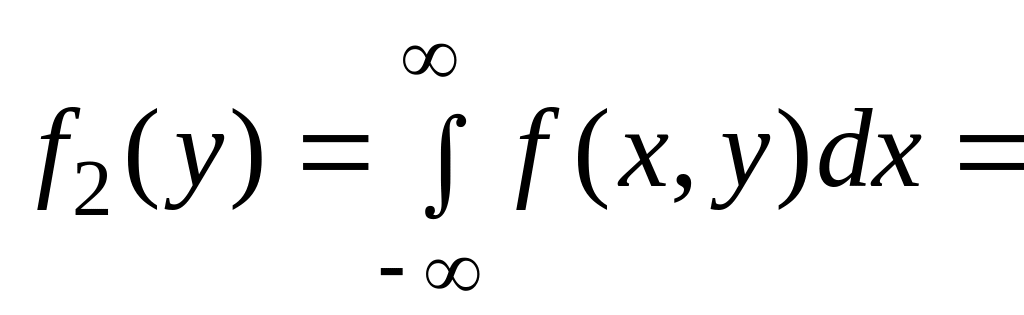
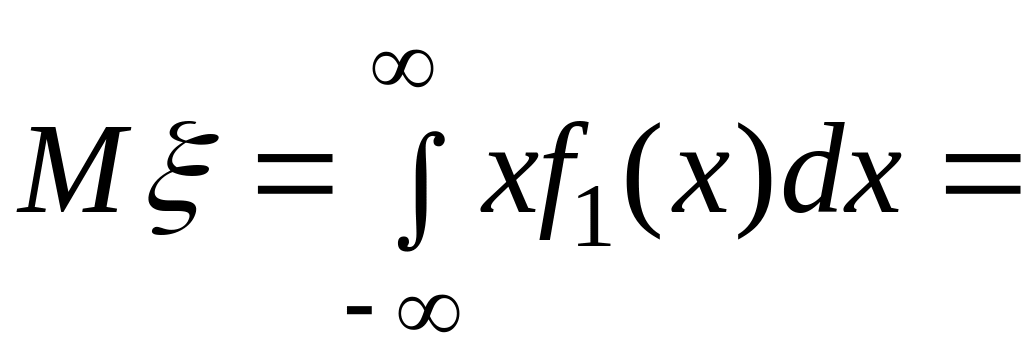
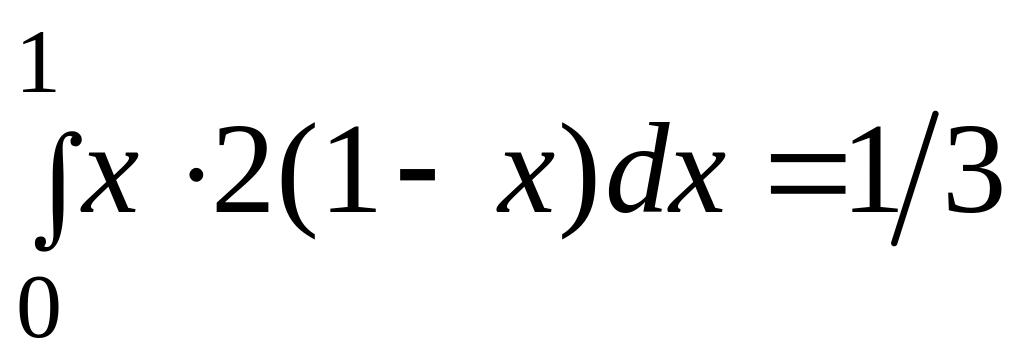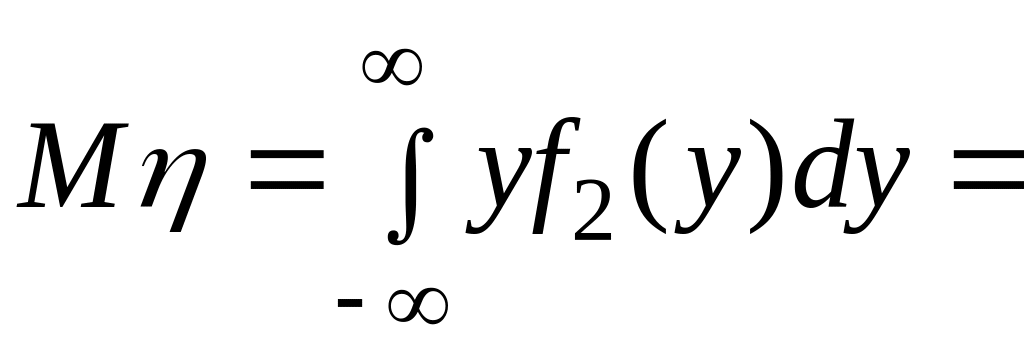
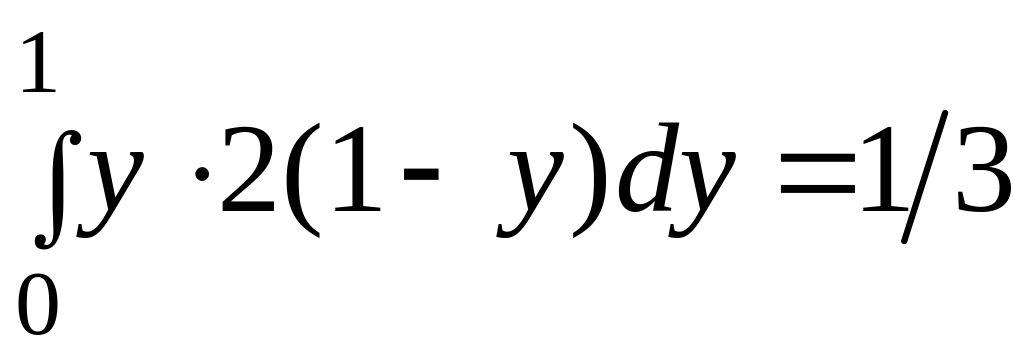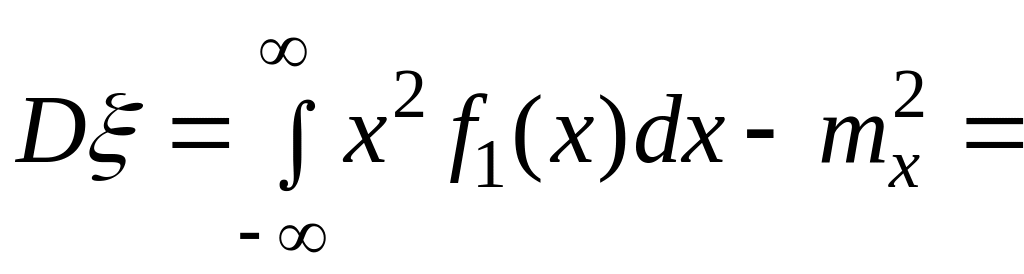
4)
.
.
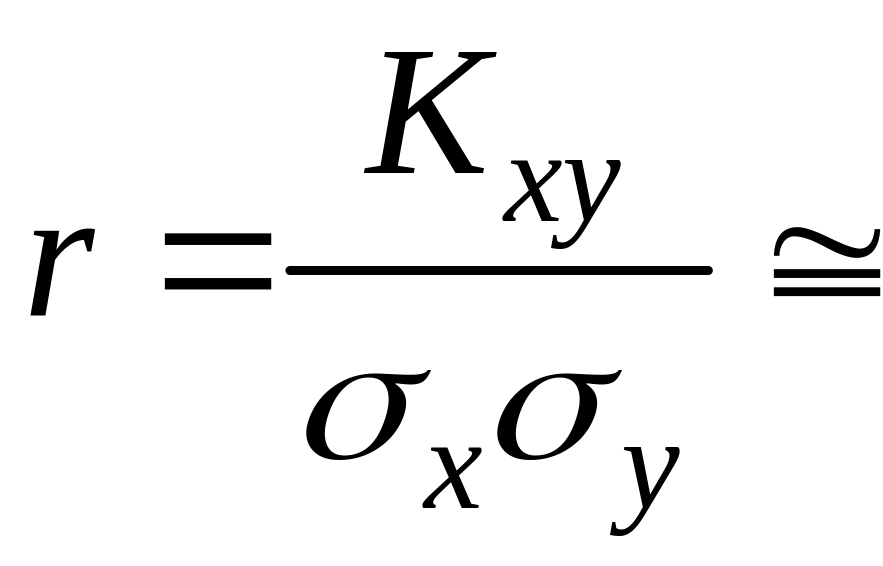
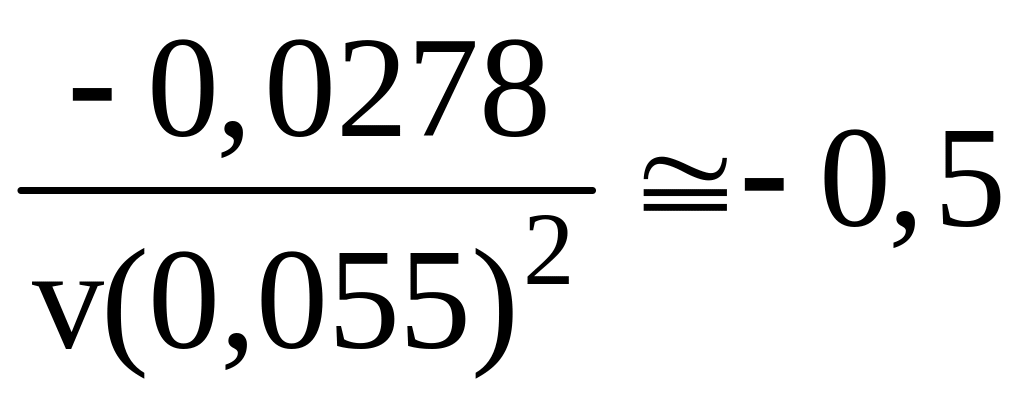5)
.
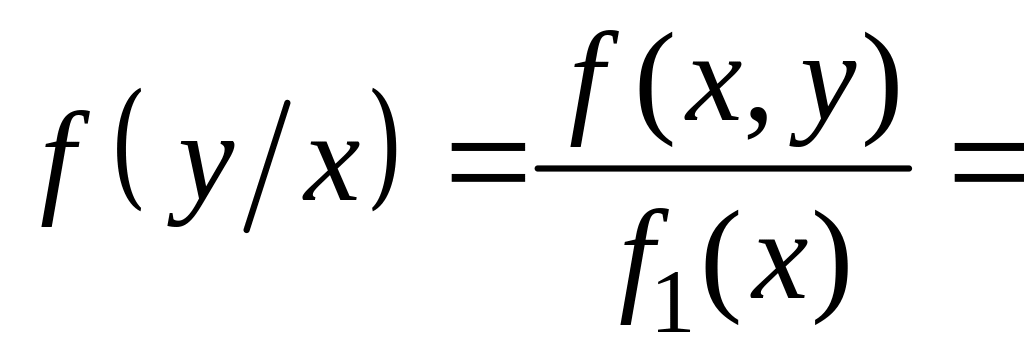
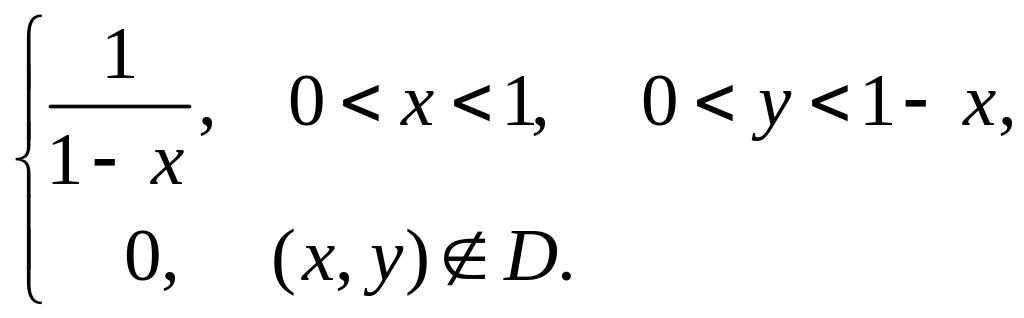
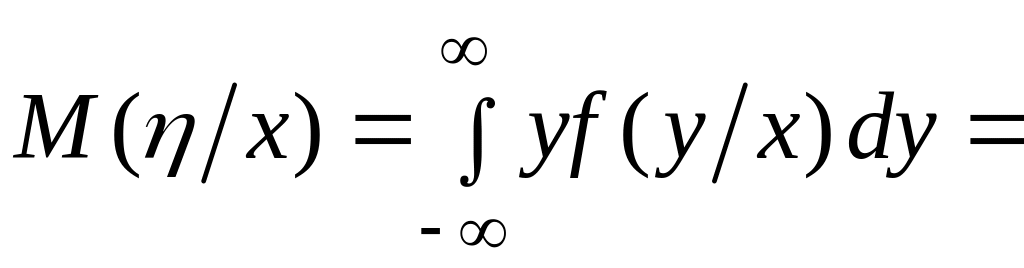
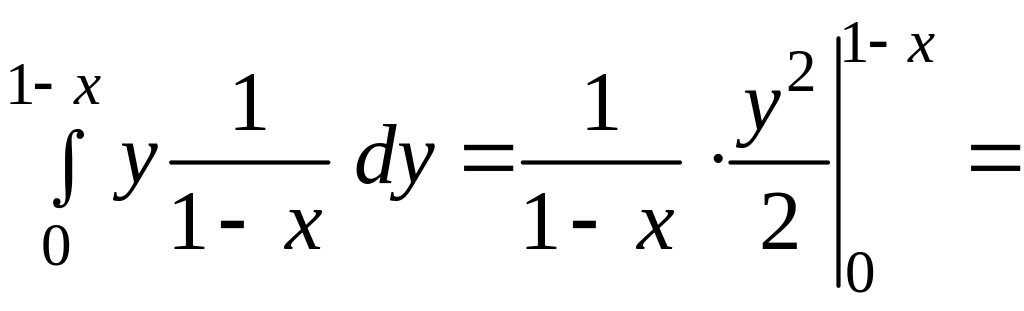
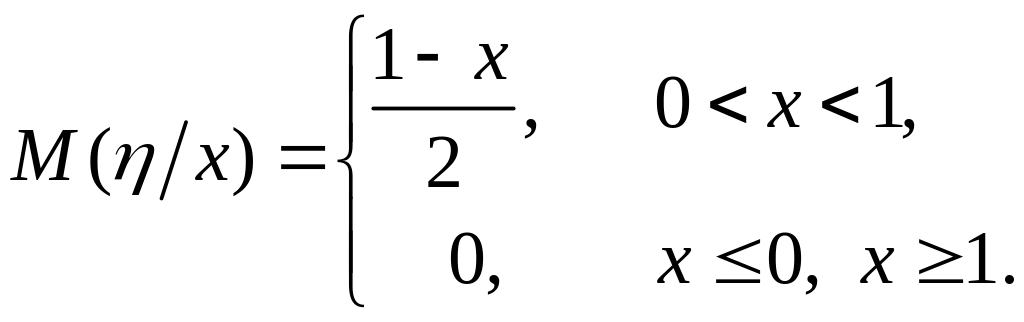
Пример 2. Дискретная двумерная случайная величина распределена по закону, приведенному в таблице
-
–1
0
2
–1
0,2
0,1
0,3
1
0,1
0,1
0,2
Определить:
1) Законы распределения составляющих и ;
2) Условный закон
распределения случайной величины
при условии, что
;
3)
;
4) Коэффициент
корреляции
.
Решение. Имеем
|
–1 |
1 |
|
0,6 |
0,4 |
|
–1 |
0 |
2 |
|
0,3 |
0,2 |
0,5 |
, 
,
,
.
|
–1 |
1 |
|
|
|
|
|
|
.
.
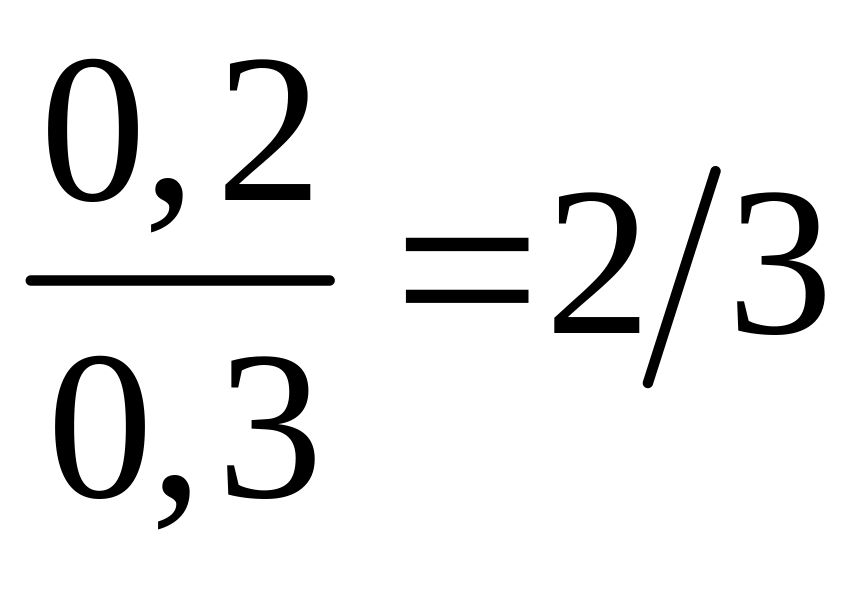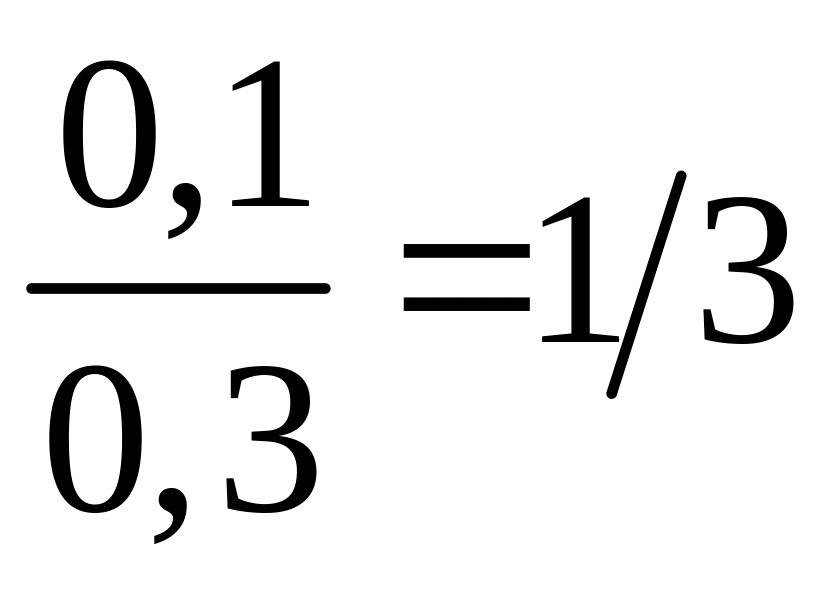Сравнивая (*) и
(**), видим, что
– зависимые случайные величины:
;
=
;
.
Пример 3. Случайная
точка
распределена равномерно внутри круга
радиуса
.
Найти математическое ожидание случайной
величины
.
Решение. Плотность распределения вероятности
=
=
.
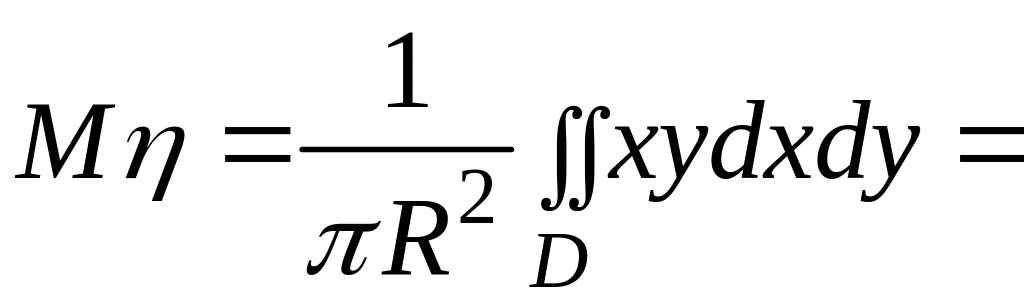
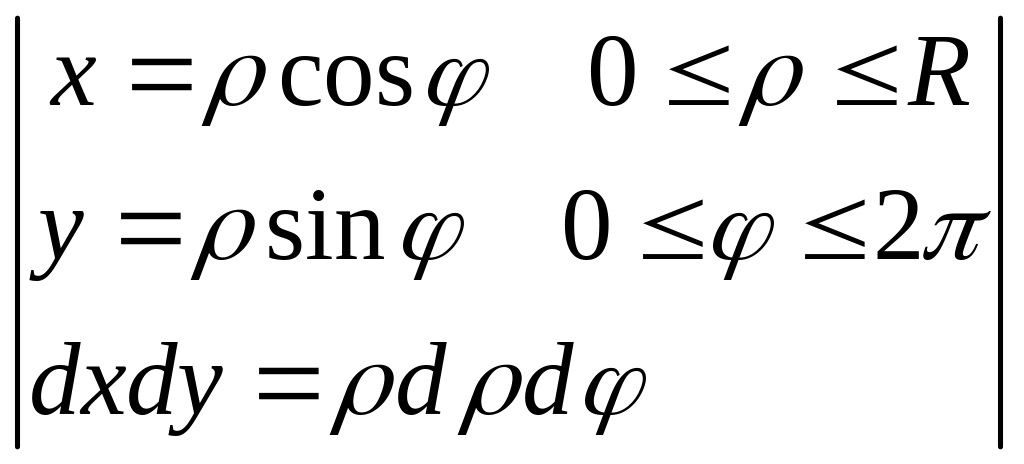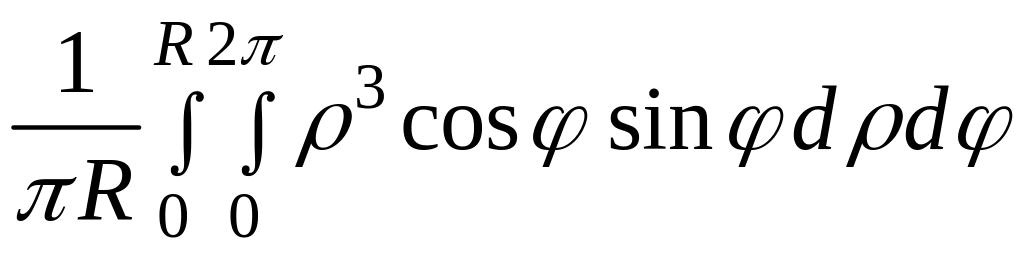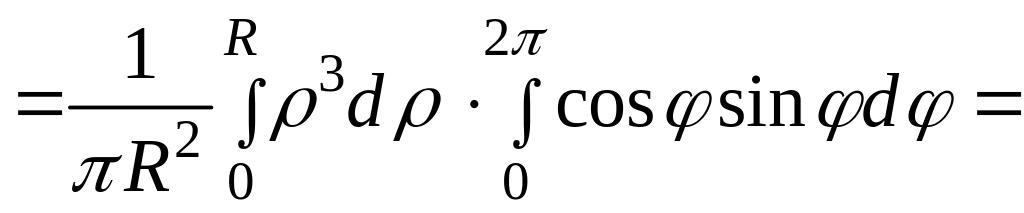
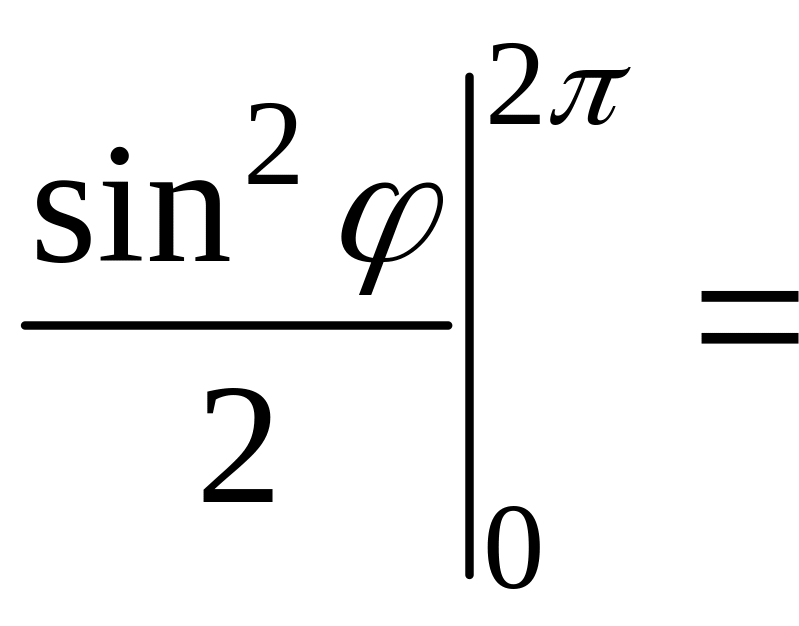
Пример 4. Пара
случайных величин
и
имеет совместное нормальное распределение
с вектором математических ожиданий
и ковариационной матрицей
:
.
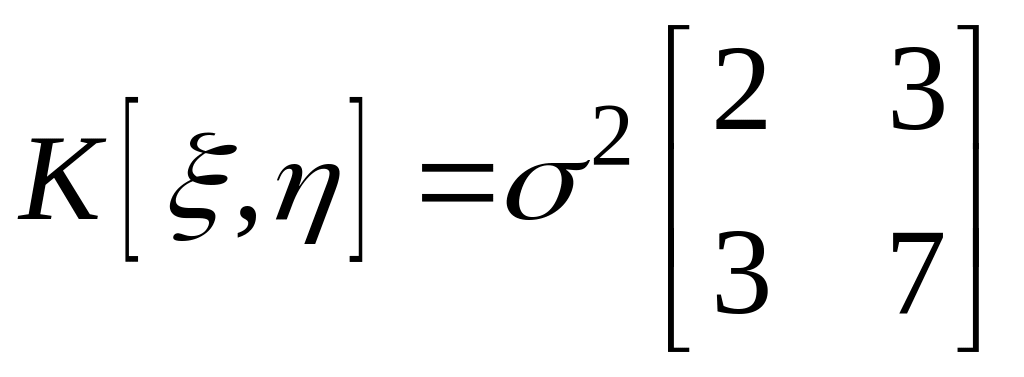Известно, что
.
Найти
.
Решение. Совместная
нормальность пары случайных величин
и
обеспечивает нормальность каждой из
них и любой их линейной комбинации, в
частности величина
нормальна с параметрами
, 
.
Подставляя в последнее соотношение элементы ковариационной матрицы
, 
, 
,
получим
.
По условию
,
откуда, используя нормальность
,
.
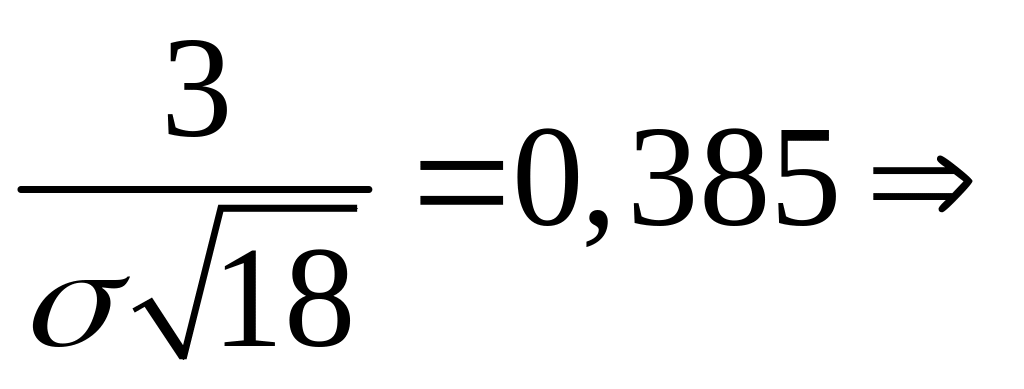
Искомые дисперсии равны, соответственно,
, 
.
Пример 5. Случайный
вектор
имеет вектор математических ожиданий
и корреляционную матрицу
.
,
.
Вычислить вектор
математических ожиданий
случайного вектора
и корреляционную матрицу вектора
.
Решение.
.
.
.
.
.
=
.
Ответ:
,
.
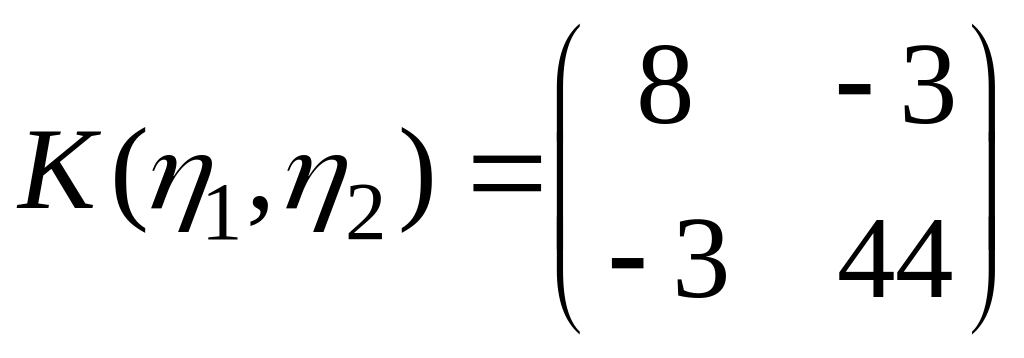