
- •1. Блок Clock (Годинник)
- •Блок Constant (Константа)
- •3.Блок Fcn (Функція)
- •4.Блок Transfer Fcn (Передавальна функція)
- •5.Блок Gain (Підсилювач)
- •6.Блок Integrator (Інтегратор)
- •7 . Блок Produkt (Множення та ділення)
- •Блок Saturation (Насичення/Обмеження)
- •Практичне заняття №1.
- •Практичне заняття №2.
- •Практичне заняття №3.
- •Практичне заняття №4.
- •Практичне заняття №5.
- •Практичне заняття № 10
- •Практичне заняття № 11
- •Xlabel('X') % метка оси ox
- •Xlabel('X') % метка оси ox
Практичне заняття №1.
1. Побудувати графік функції
а)
![]()
Наведемо блок-схему для побудови графіка цієї функції
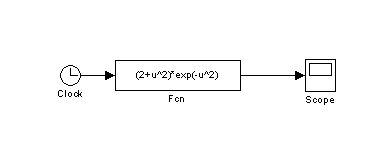
Графік функції
на проміжку
![]() має вигляд
має вигляд
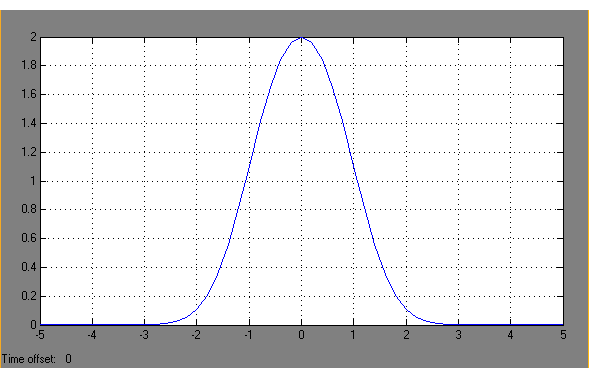
б)
![]()
Наведемо блок-схему для побудови графіка цієї функції
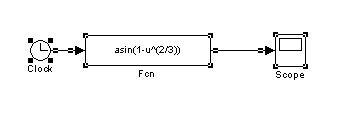
Графік функції
на проміжку
![]() має вигляд
має вигляд
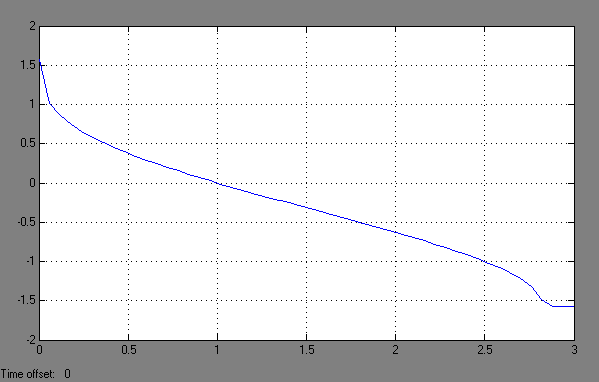
в)
![]()
Наведемо блок-схему для побудови графіка цієї функції
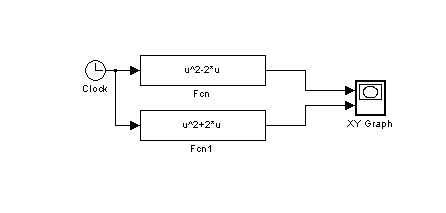
Графік функції
на проміжку
![]() має вигляд
має вигляд
г)
![]()
Наведемо блок-схему для побудови графіка цієї функції
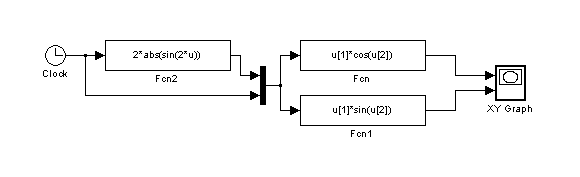
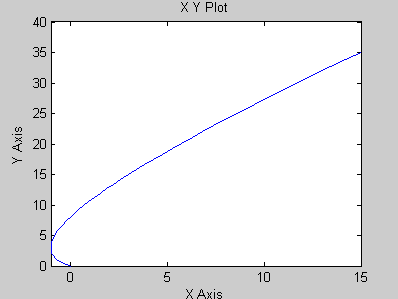
Графік функції
на проміжку
![]() має вигляд
має вигляд
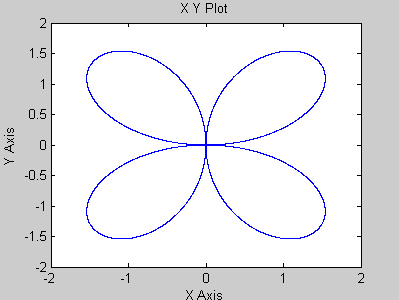
Варіанти завдання:
а) ; б) ; в) ; г)
а)
 ;
б)
;
б)
 ;
в)
;
в)
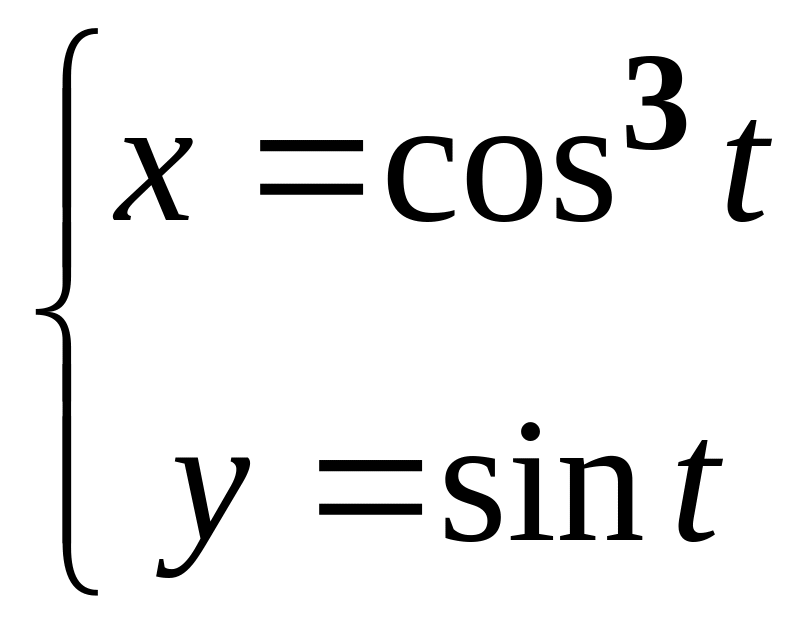 ;
г)
;
г)
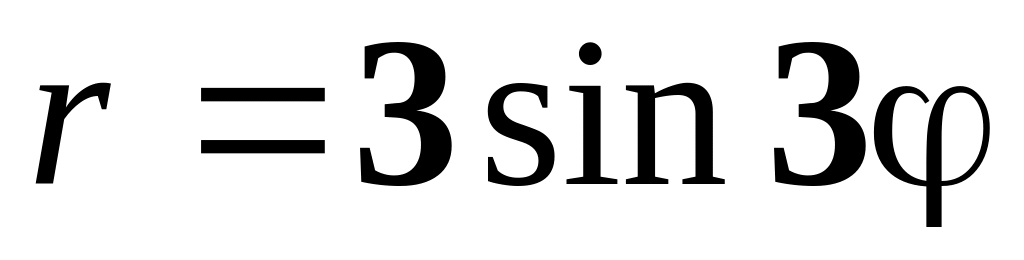
а)
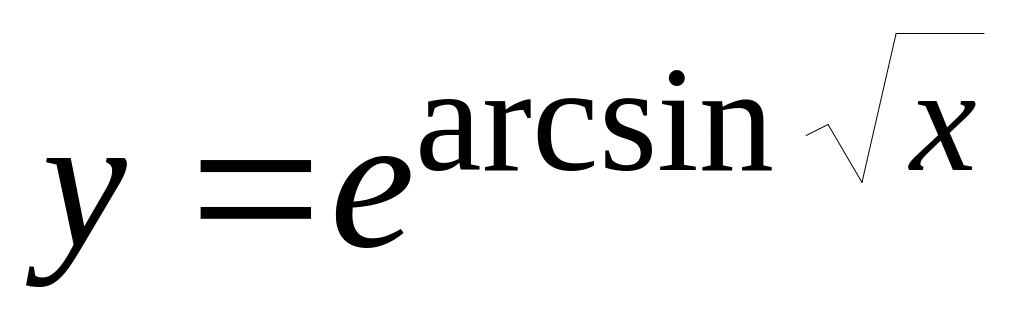 ;
б)
;
б)
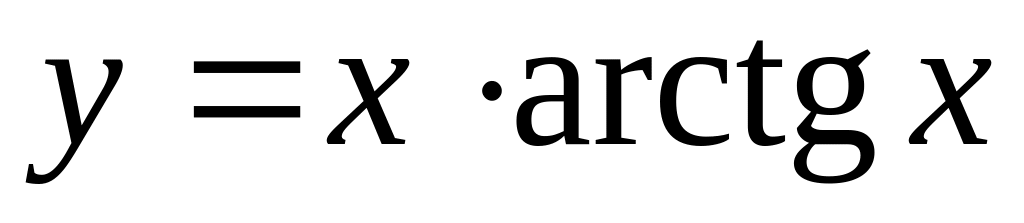 ;
в)
;
в)
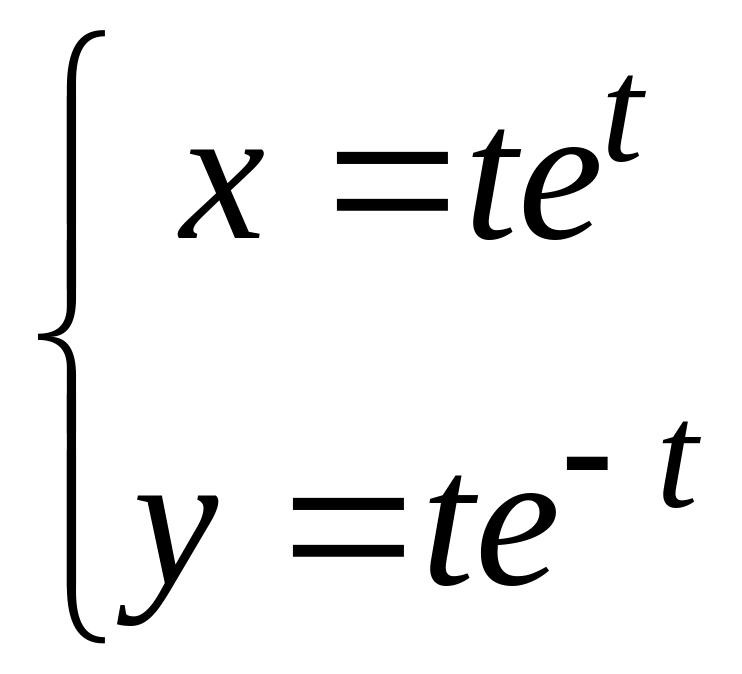 ;
г)
;
г)

а)
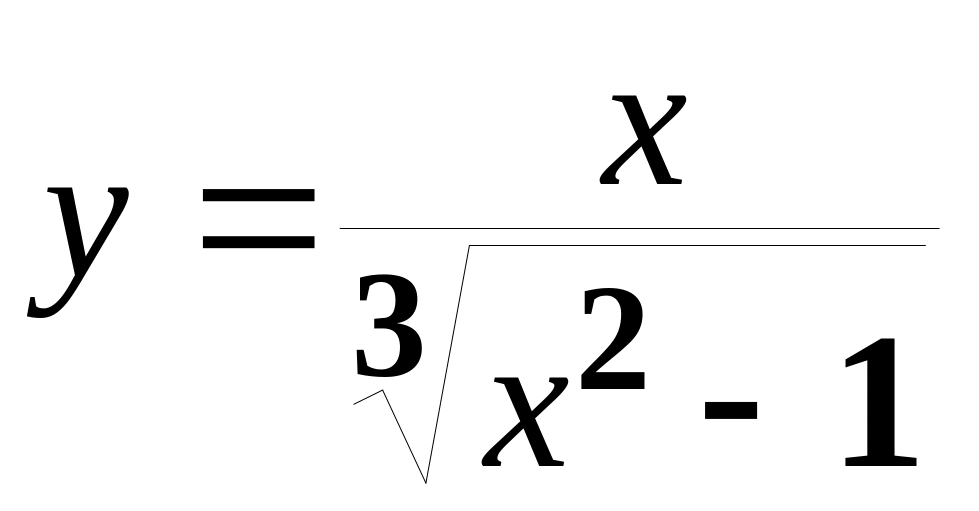 ;
б)
;
б)
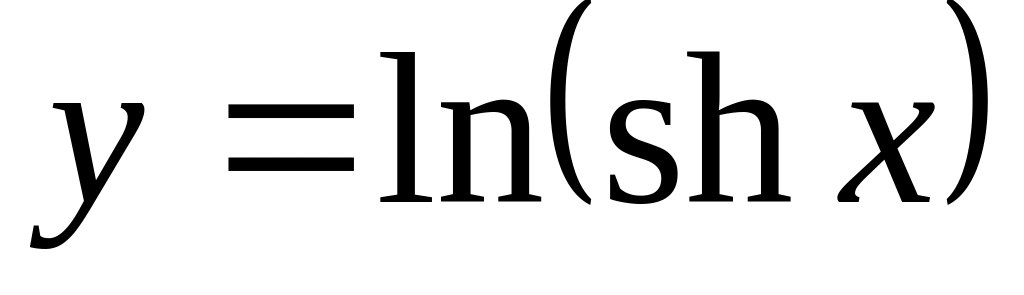 ;
в)
;
в)
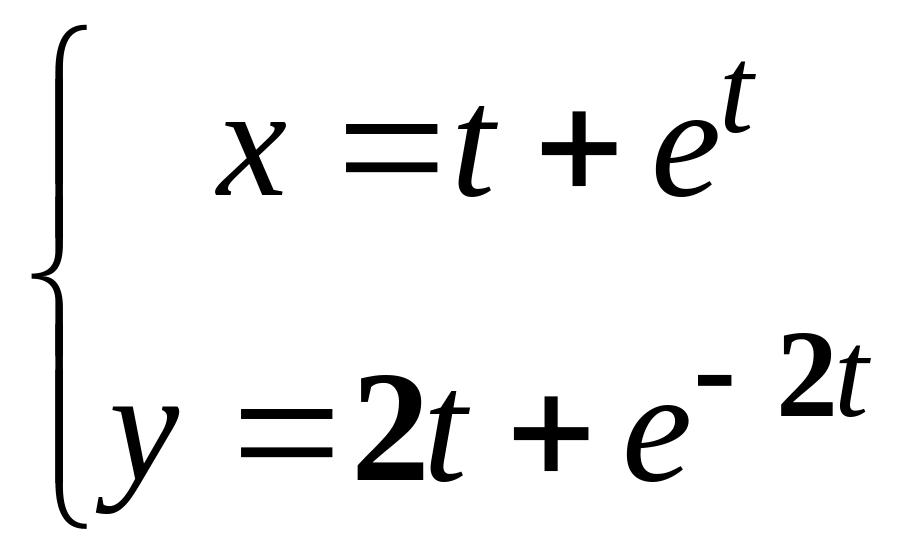 ;
г)
;
г)

а)
 ;
б)
;
б)
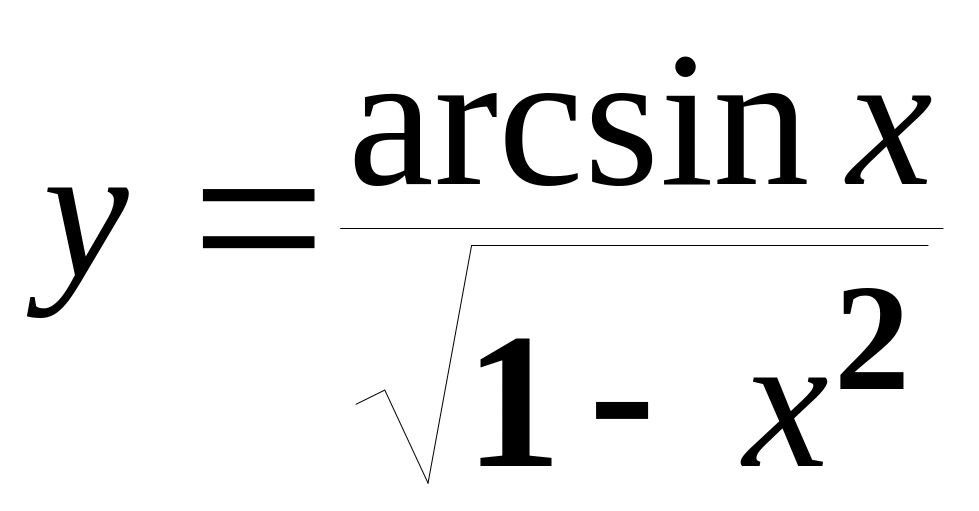 ;
в)
;
в)
 ;
г)
;
г)

а)
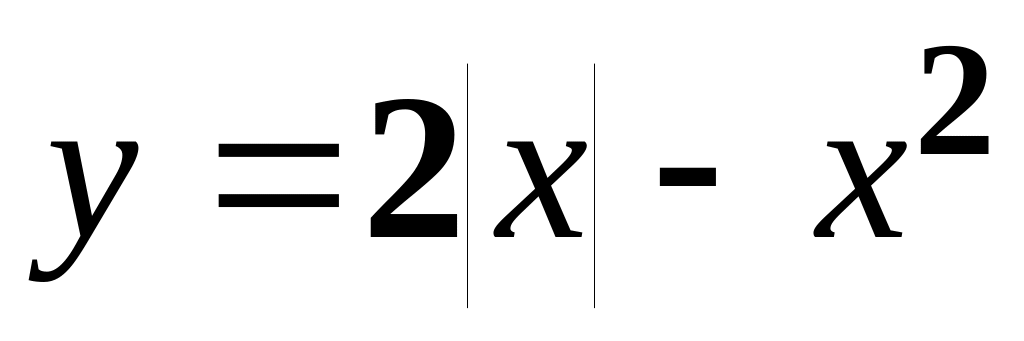 ;
б)
;
б)
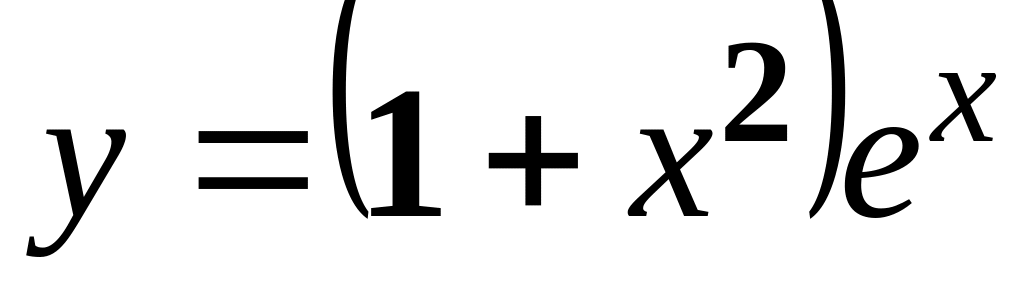 ;
в)
;
в)
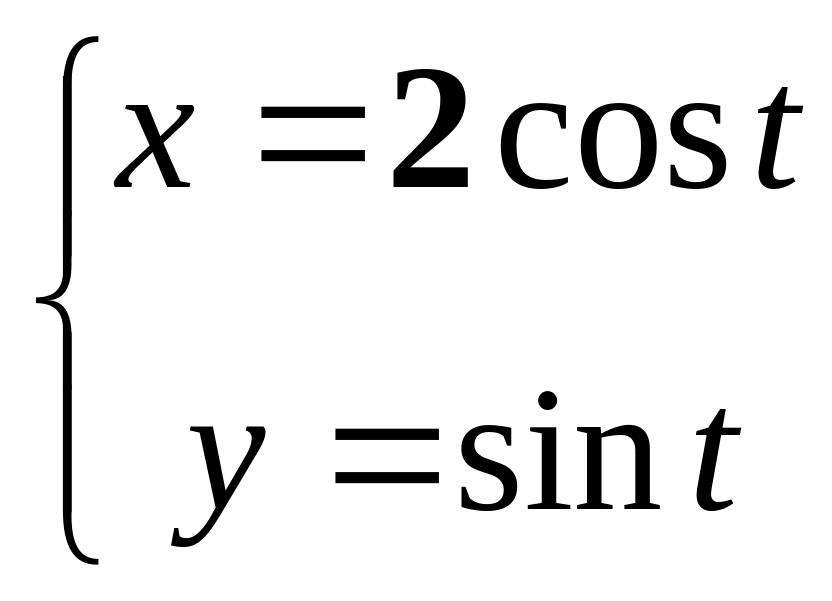 ;
г)
;
г)

а)
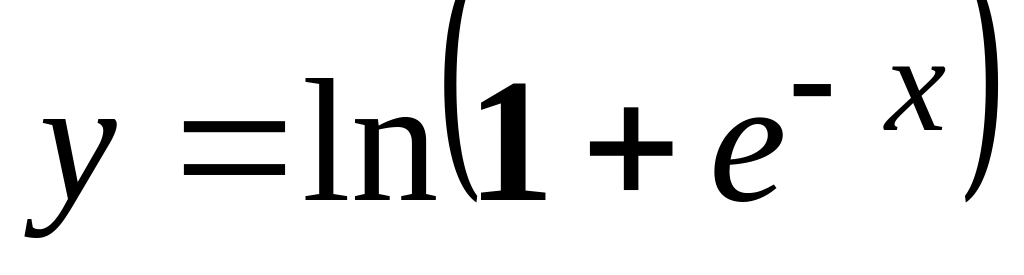 ;
б)
;
б)
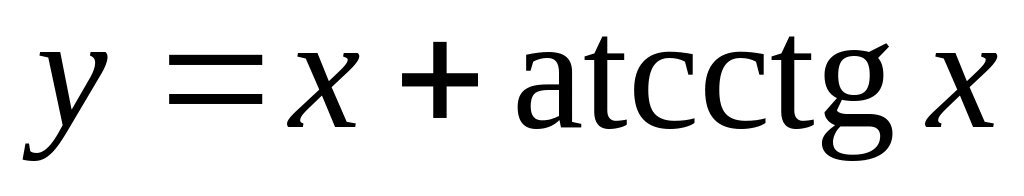 ;
в)
;
в)
 ;
г)
;
г)
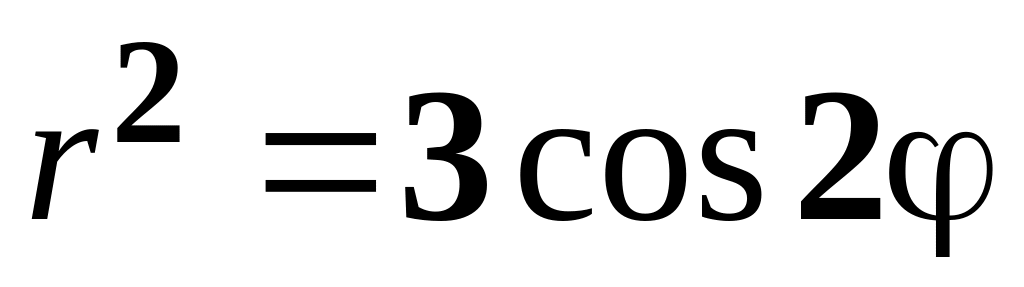
а)
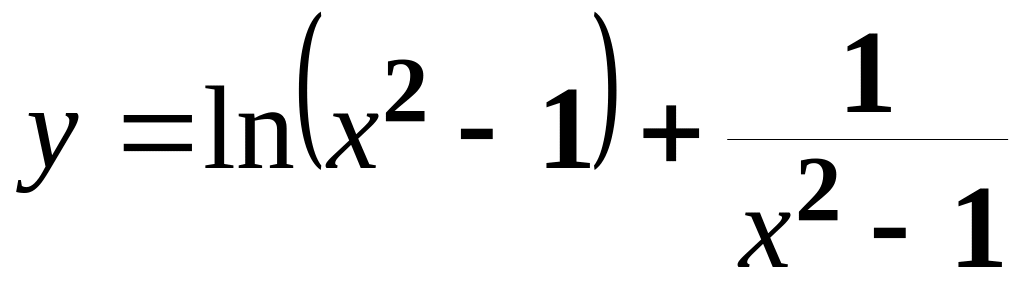 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

а)
 ;
б)
;
б)
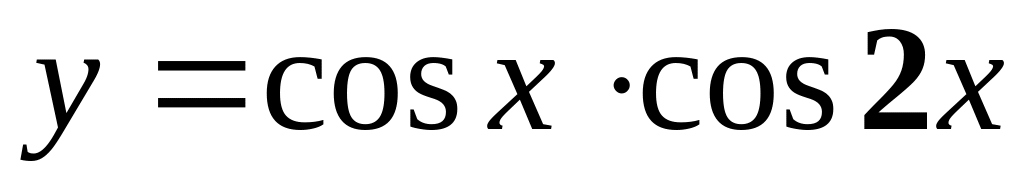 ;
в)
;
в)
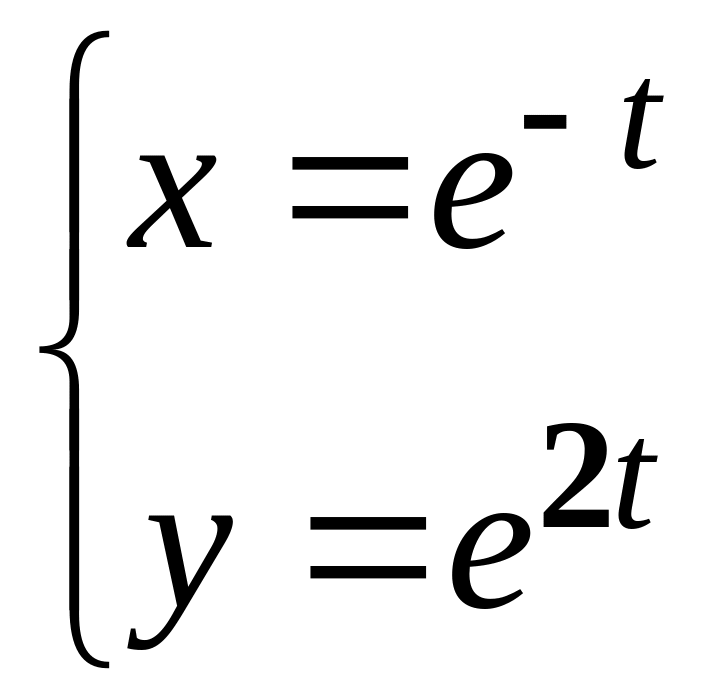 ;
г)
;
г)
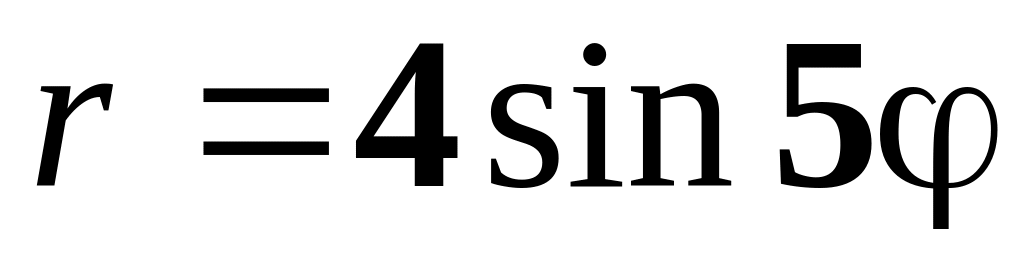
а)
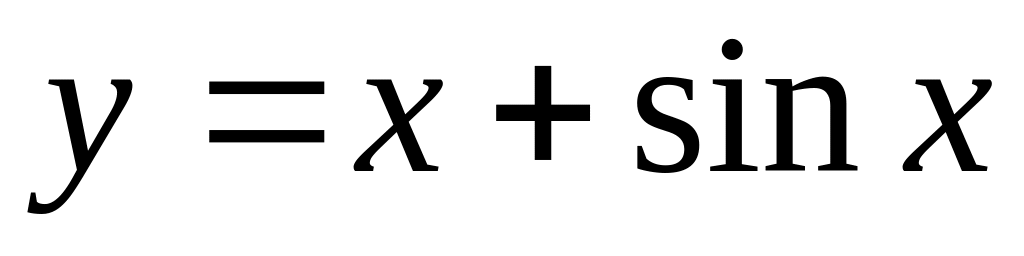 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
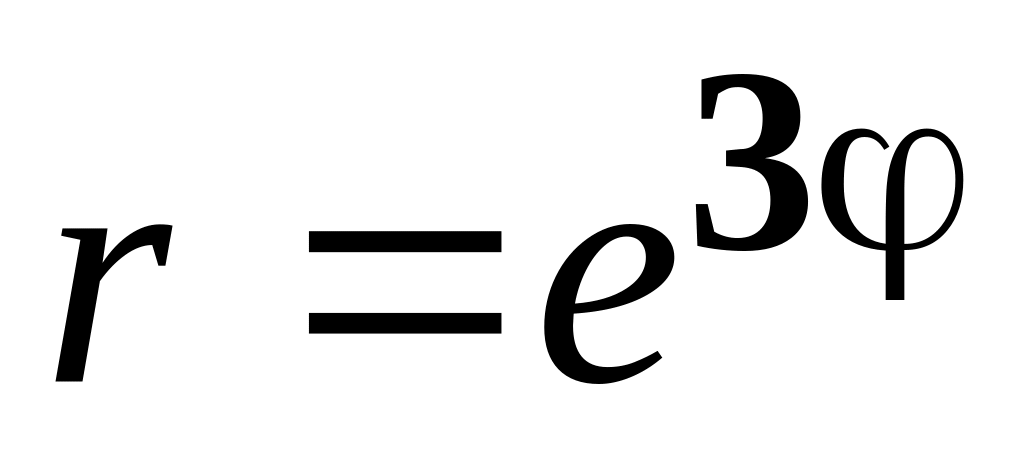
а)
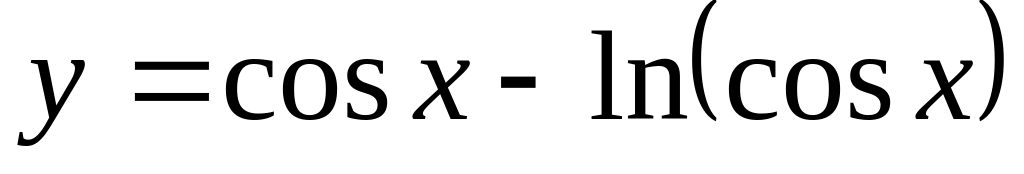 ;
б)
;
б)
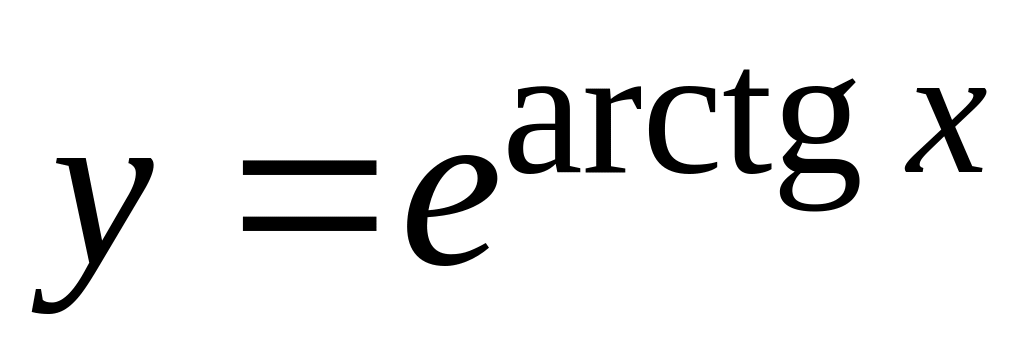 ;
в)
;
в)
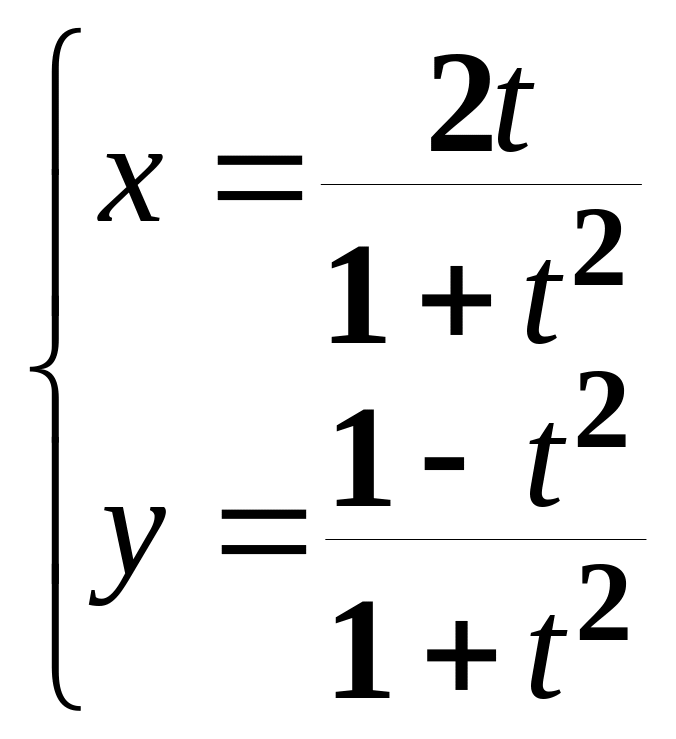 ;
г)
;
г)

а)
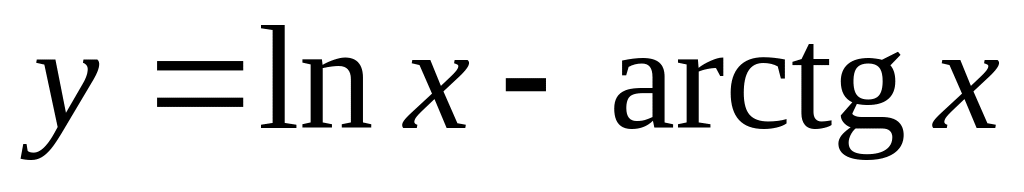 ;
б)
;
б)
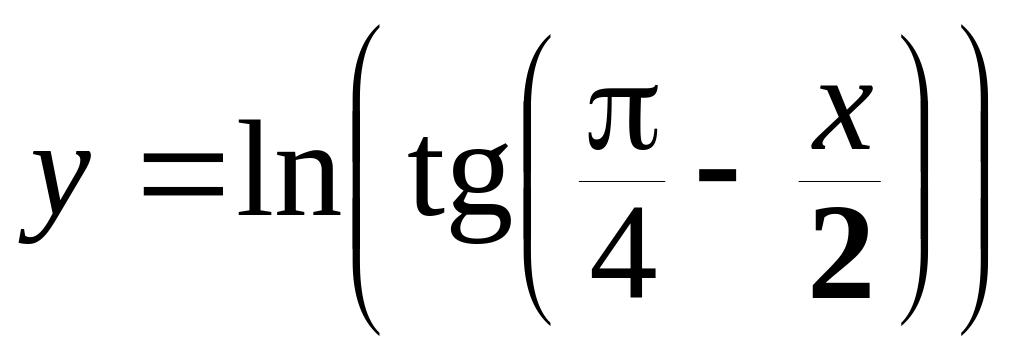 ;
в)
;
в)
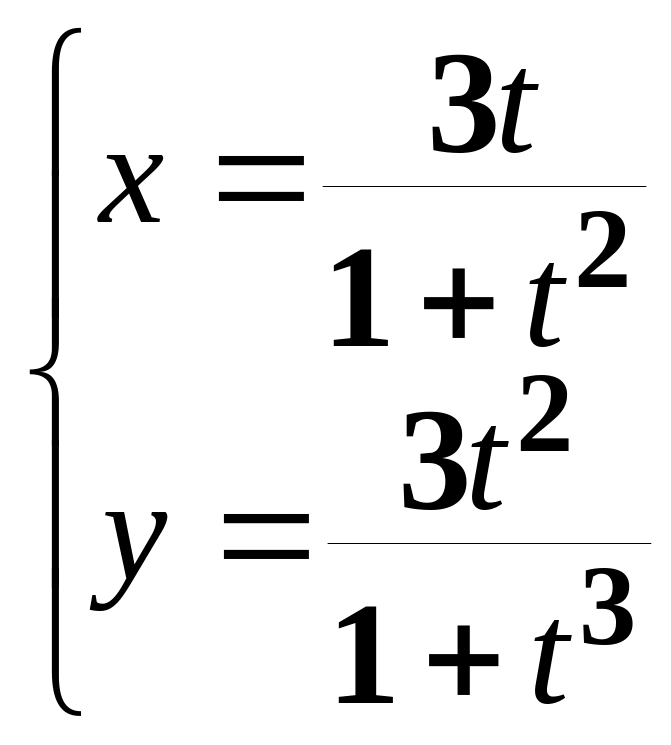 ;
г)
;
г)

а)
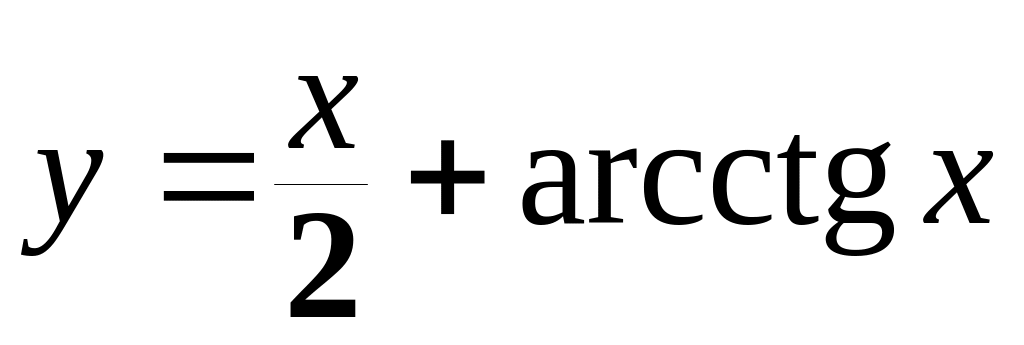 ;
б)
;
в)
;
б)
;
в)
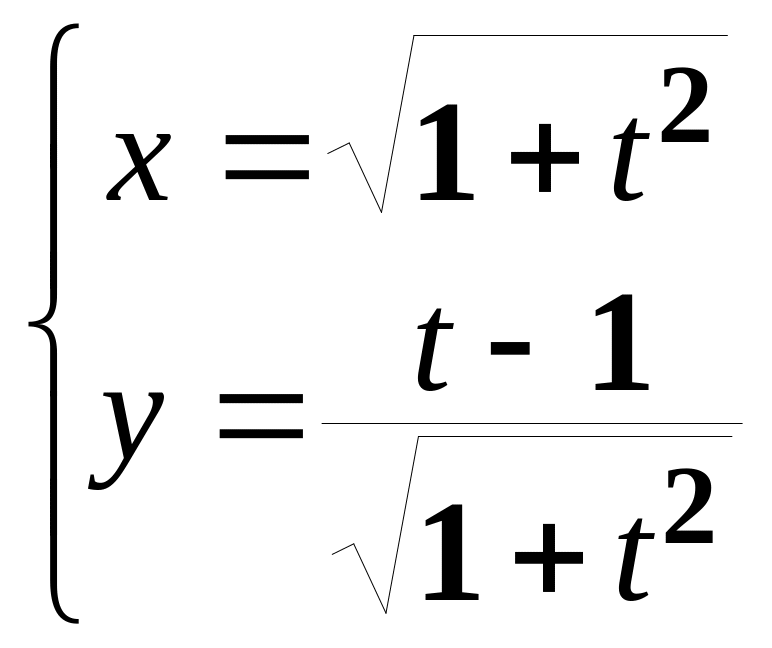 ;
г)
;
г)

а)
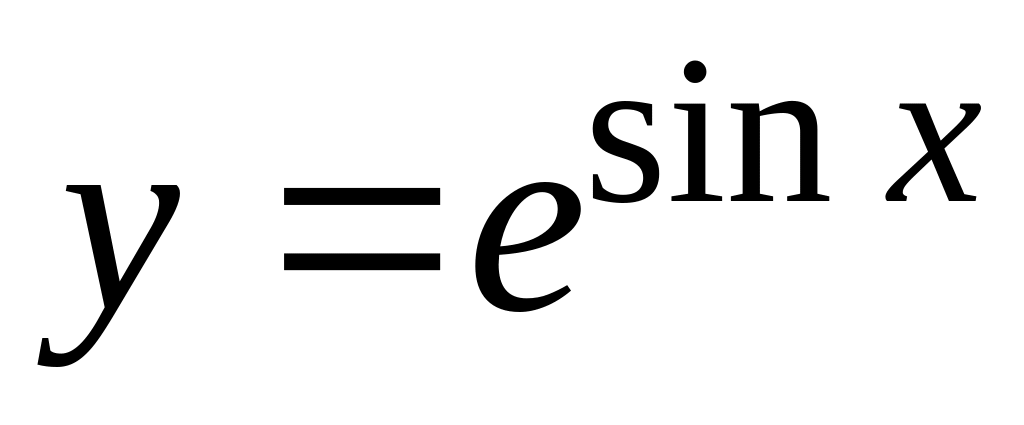 ;
б)
;
б)
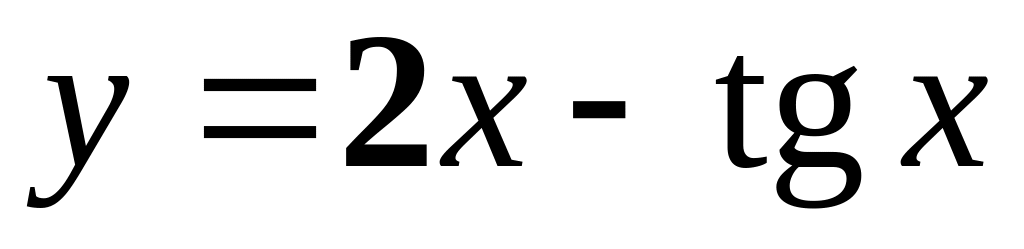 ;
в)
;
в)
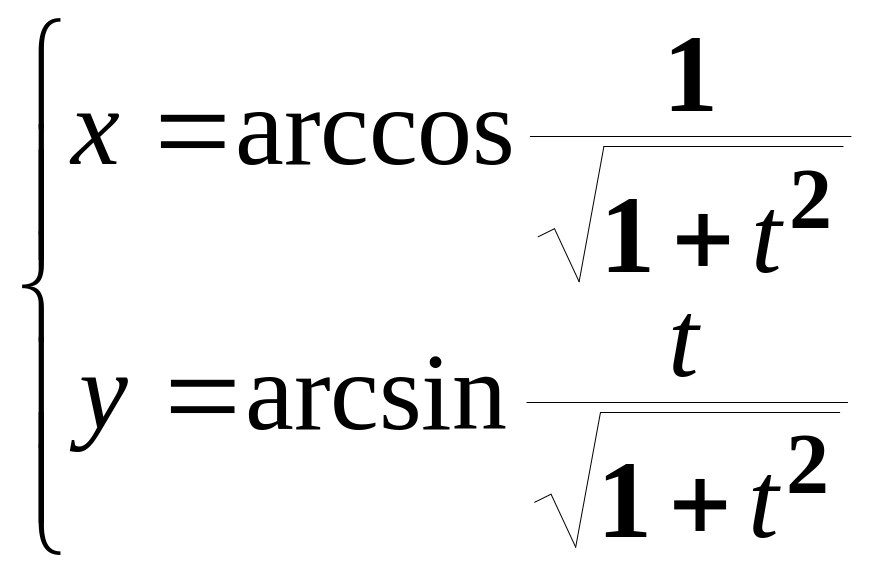 ;
г)
;
г)
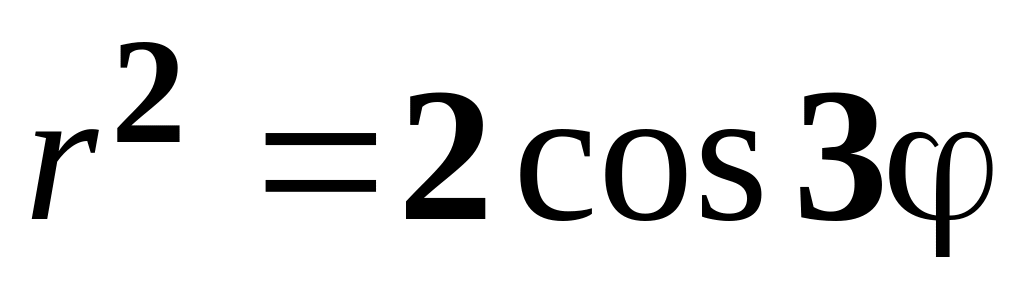
а)
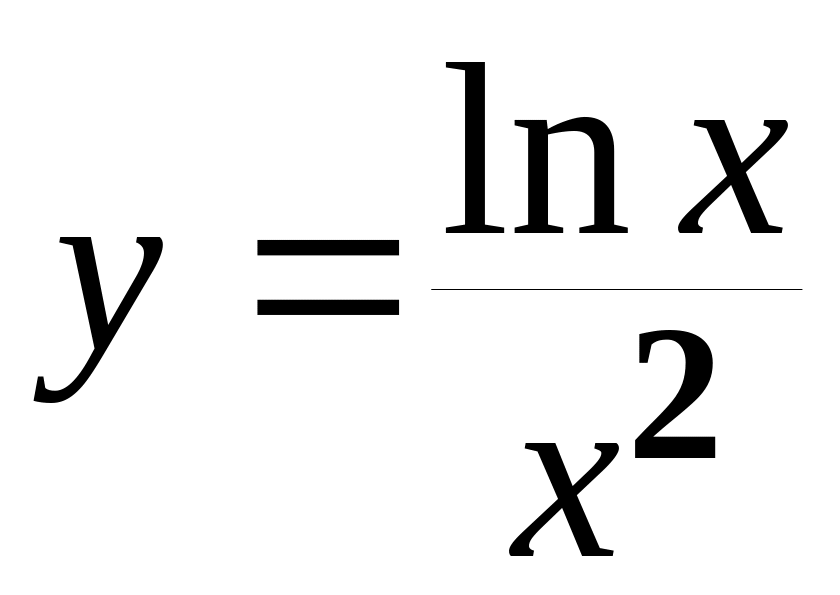 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

Практичне заняття №2.
Розв’язати лінійне диференціальне рівняння з нульовими початковими умовами за допомогою передавальної функції
![]() .
.
Похідна
![]() відповідає виразу
відповідає виразу
![]() .
Запишемо
дане рівняння у вигляді:
.
Запишемо
дане рівняння у вигляді:
![]() ,
,
тоді
![]() .
.
де
![]() -
передавальна функція (transfer fcn).
-
передавальна функція (transfer fcn).
Блок-схема для даного диференціального рівняння
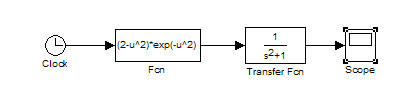
Графік розв’язку:
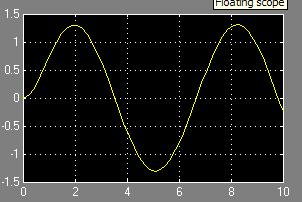
Варіанти завдання:
1.
![]() ;
2.
;
2.
![]() ; 3.
; 3.
![]()
4.
![]() ;
5.
;
5.
![]() ; 6.
; 6.
![]()
7.
![]() ;
8.
;
8.
![]() ; 9.
; 9.
![]()
10.
![]() ;
11.
;
11.
![]() ; 12.
; 12.
![]()
13.
![]() ;
14.
;
14.
![]() ; 15.
; 15.
![]()
Практичне заняття №3.
Розв’язати лінійне однорідне диференціальне рівняння з ненульовими початковими умовами за допомогою оператора Integrator
![]() .
.
В даному
рівнянні
![]() .
Початкові умови задовольняються за
допомогою оператора
Integrator. Так
як початкові умови задані при
.
Початкові умови задовольняються за
допомогою оператора
Integrator. Так
як початкові умови задані при
![]() ,
то в вкладке
Simulation parameters
меняем значение параметра Star
time с
,
то в вкладке
Simulation parameters
меняем значение параметра Star
time с
![]() на
на
![]() .
Така блок-схема має вигляд:
.
Така блок-схема має вигляд:
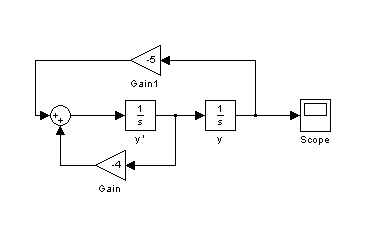
Графік розв’язку задачі Коші:
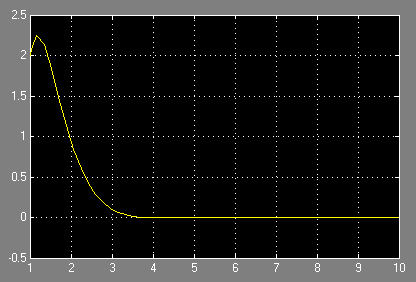
Варіанти завдання:
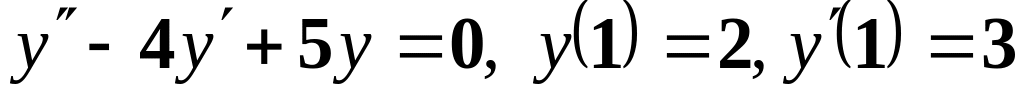 ;
;
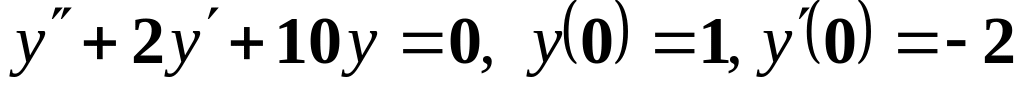 ;
;
 ;
;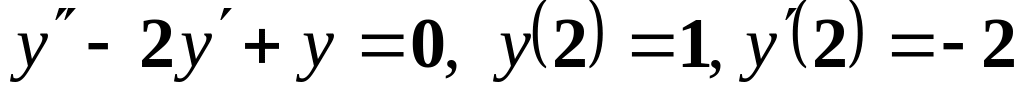 ;
;
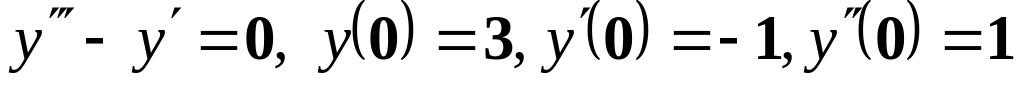 ;
;
 ;
;
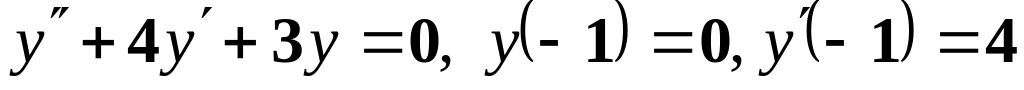 ;
;
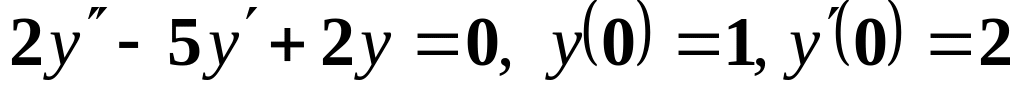 ;
;
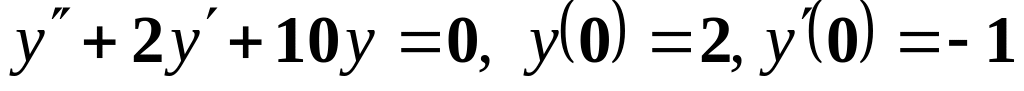 ;
;
 ;
;
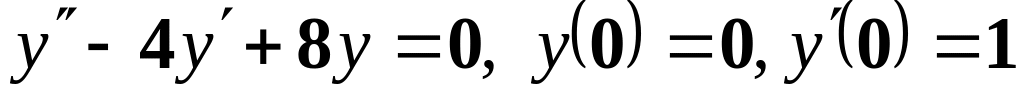 ;
;
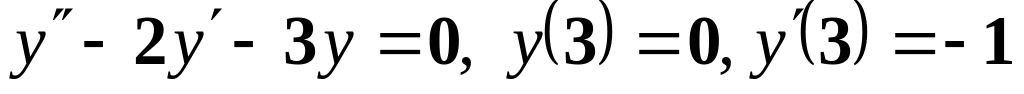 ;
;
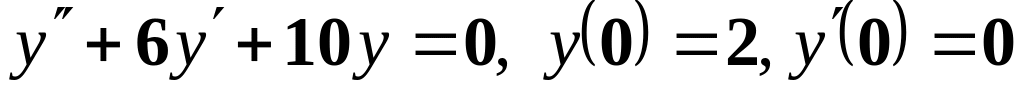 ;
;
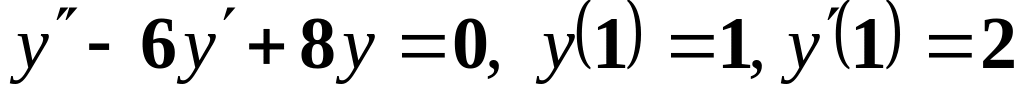 ;
;
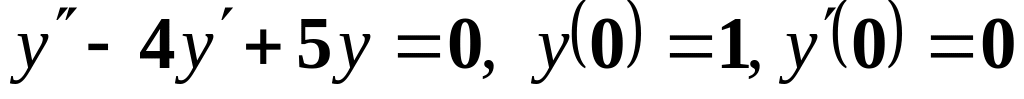 ;
;
Практичне заняття №4.
Розв’язати лінійне неоднорідне диференціальне рівняння з ненульовими початковими умовами за допомогою оператора Integrator
![]() .
.
Виражаємо старшу похідну:
![]() .
Усі дані вносимо в блок-схему:
.
Усі дані вносимо в блок-схему:
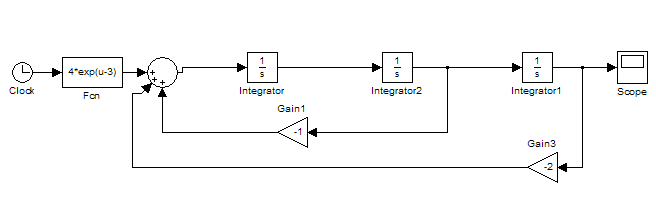
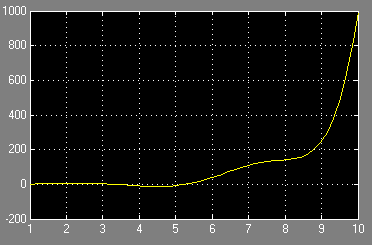
Варіанти завдання:
Практичне заняття №5.
Розв’язати однорідне диференціальне рівняння з заданими початковими умовами за допомогою оператора Integrator:
![]()
Так як
![]() ,
то у блок-схему вносяться наступні
данні:
,
то у блок-схему вносяться наступні
данні:
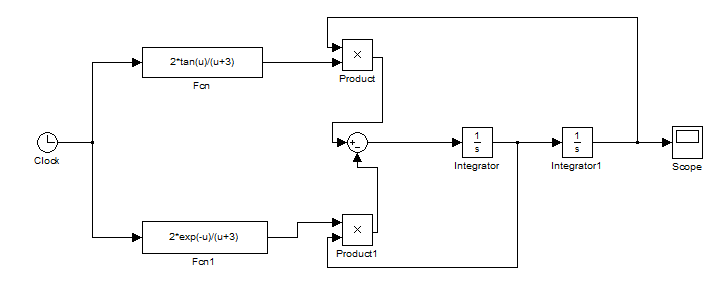
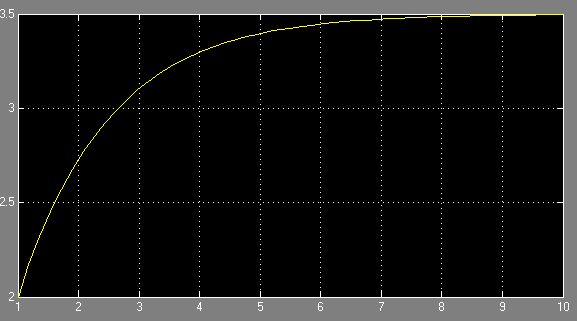
Варіанти завдання:
Практичне заняття №6.
Розв’язати неоднорідне диференціальне рівняння з заданими початковими умовами за допомогою оператора Integrator
![]() .
.
З даного рівняння маємо:
![]()
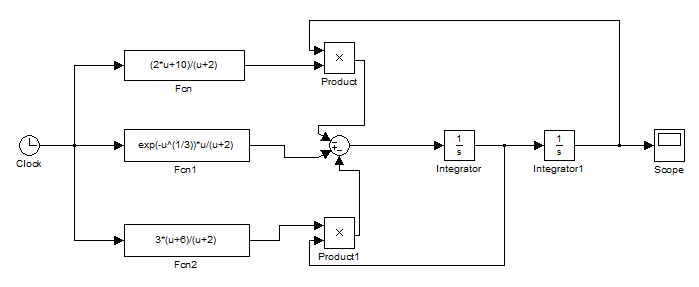
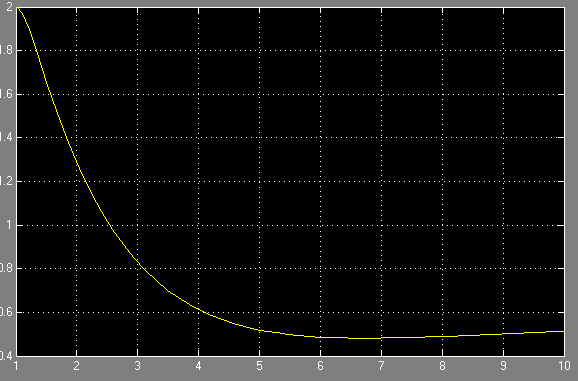
Варіанти завдання:
Практичне заняття №7.
Розв’язати однорідну систему диференціальних рівнянь з заданими початковими умовами.
 ;
;
Блок-схема:

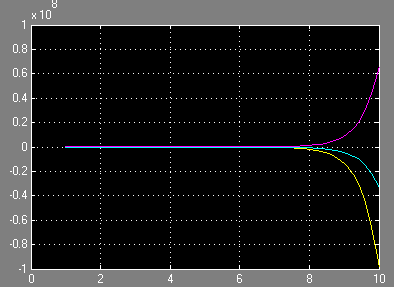
Варіанти завдання:
1.
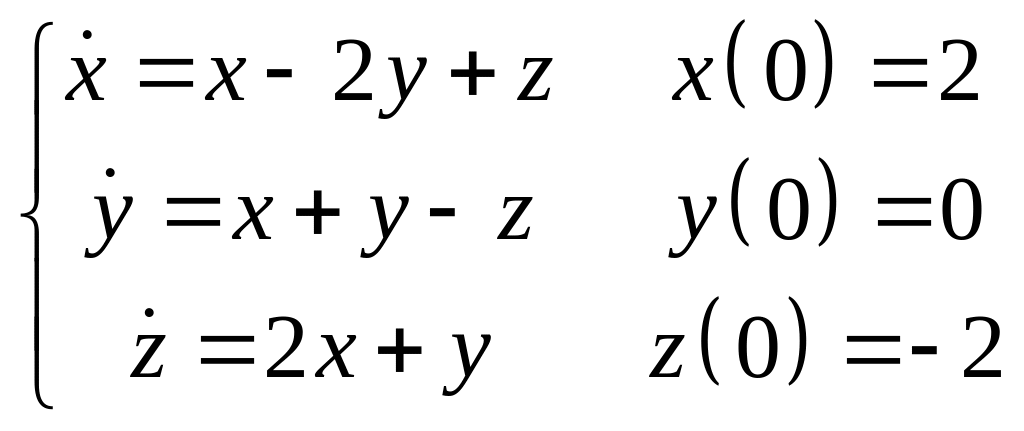 2.
2.

3.
 4.
4.
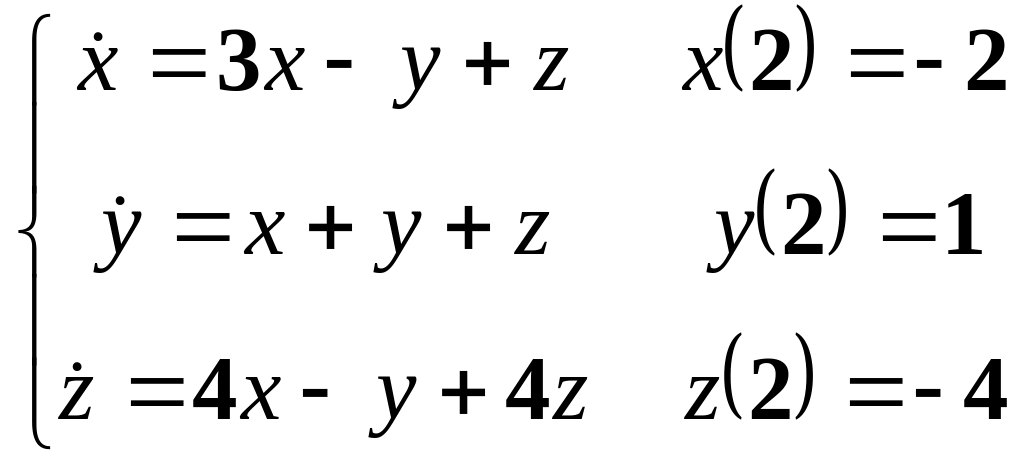
 6.
6.
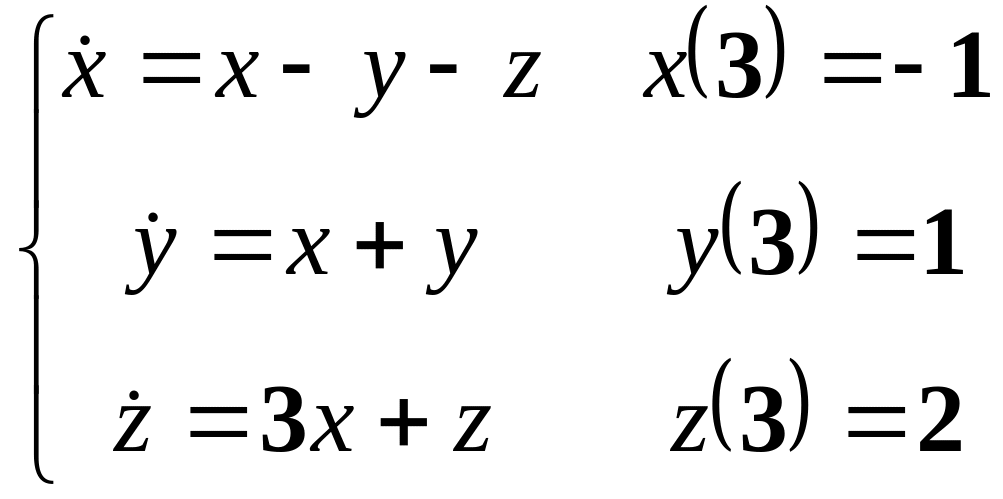
7.
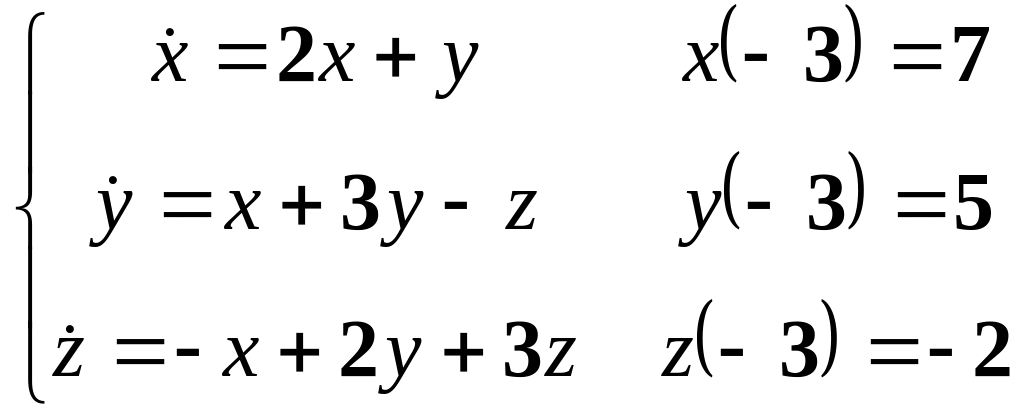 8.
8.
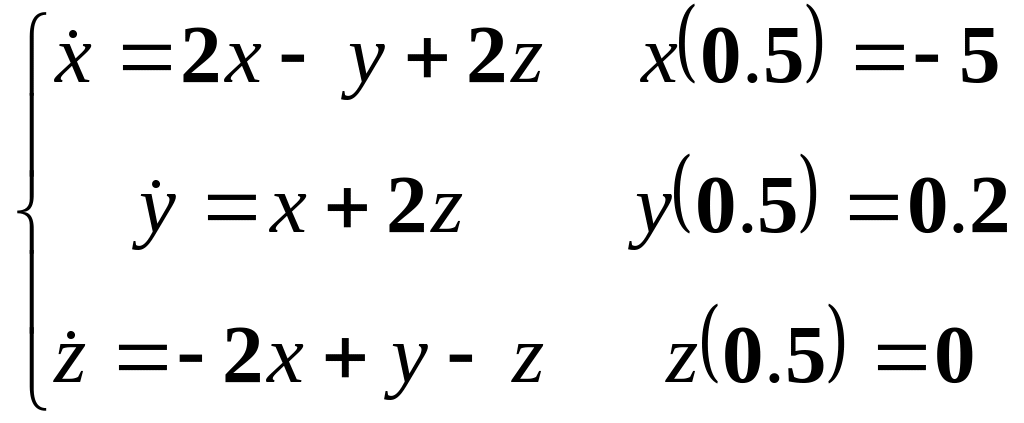
9.
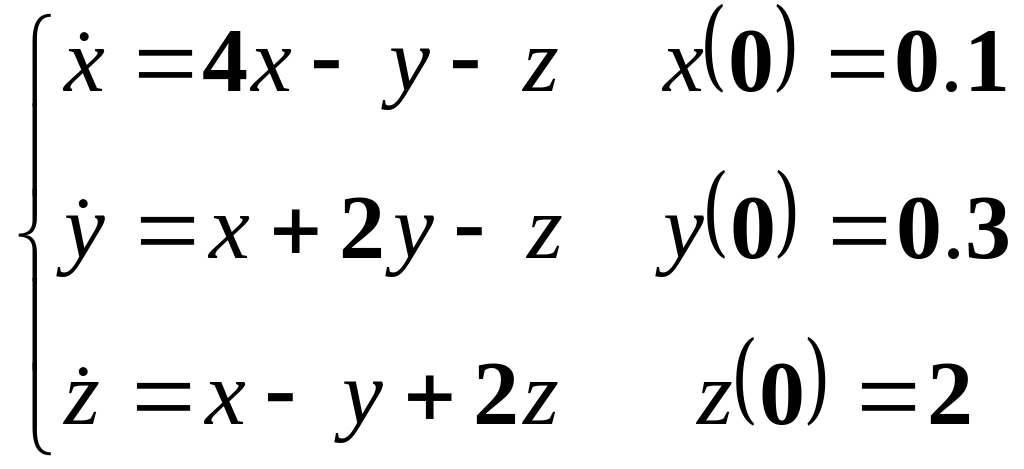 10.
10.
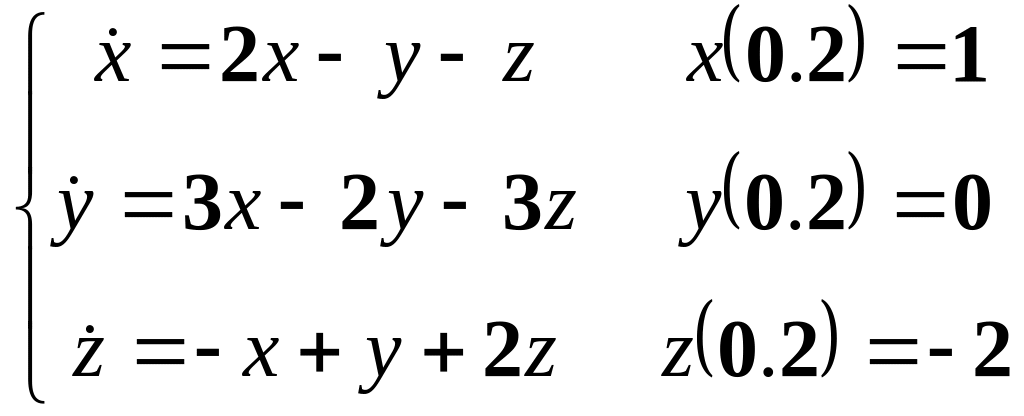
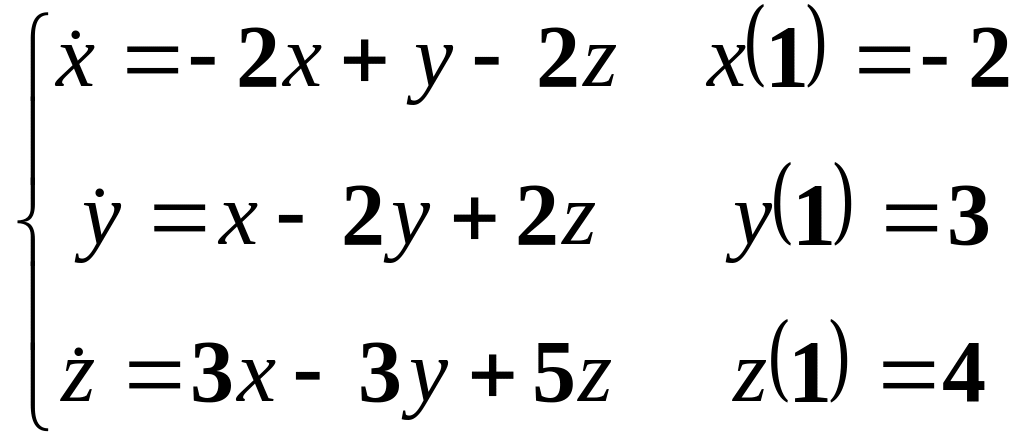 12.
12.
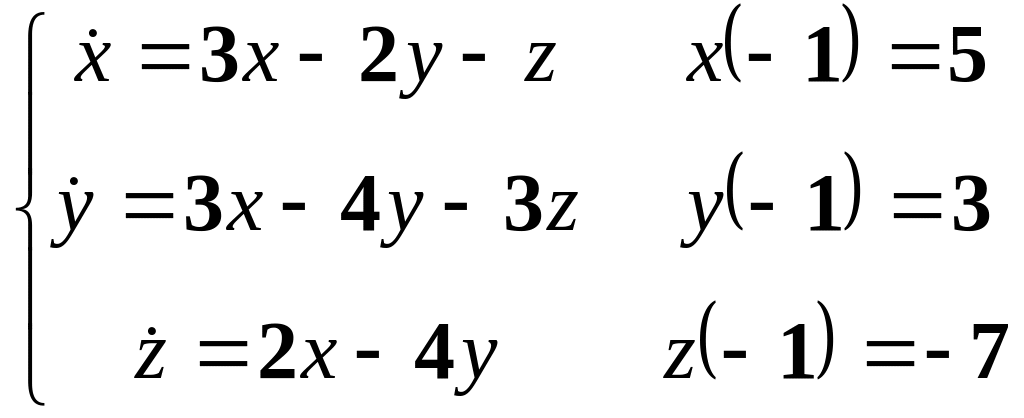
13.
 14.
14.

15.

Практичне заняття №8.
Розв’язати неоднорідну систему диференціальних рівнянь з заданими початковими умовами.
![]()
Блок-схема
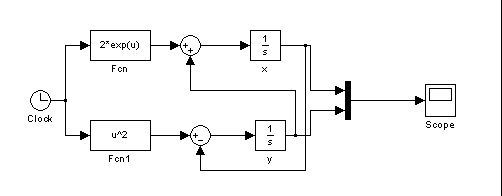
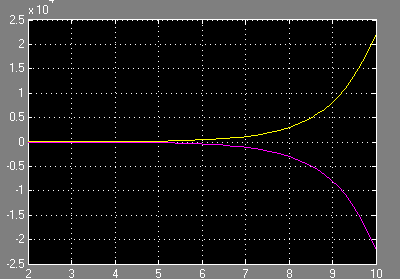
Варіанти завдання:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.

11.
12.
![]()
13.
![]() 14.
14.

15.
![]()
Практичне заняття № 9
Моделювання гальмування судна в середовищі Matlab-Simulink
Рух гальмування судна описується рівнянням

У цій
моделі
чотири блоки
констант
служать
для запису
в ці
блоки
відповідних
значень
![]() ,
,
![]() ,
,
![]() ,
и
,
и
![]() .
Наступний блок mux
формує з цих констант и поточного
значення швидкості
судна
.
Наступний блок mux
формує з цих констант и поточного
значення швидкості
судна
![]() вектор
вектор
![]() з
компонентами
з
компонентами
![]() .
.
![]()
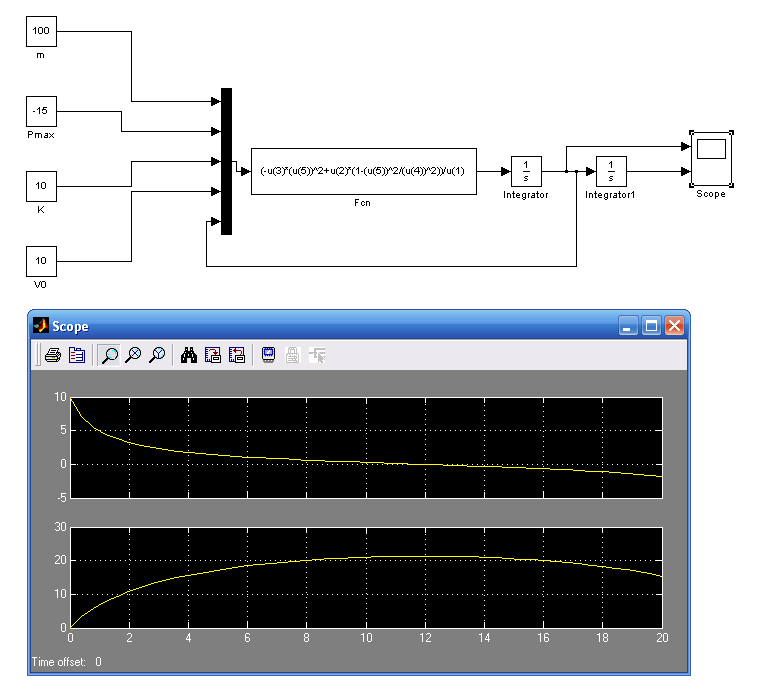
Варіанти завдань:
Скласти модель гальмування судна, користуючись рівнянням
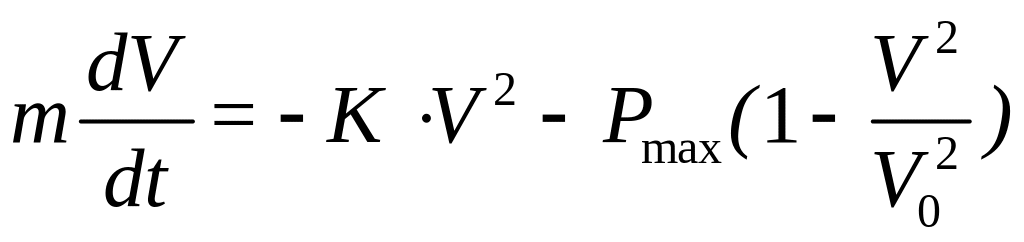 .
.
Знайти залежність швидкості і шляху від часу при активному або пасивному гальмуванні судна.

