
- •1. Основные термины и определения
- •2. Отказы технических устройств
- •2.1 Виды энергии, приводящие к отказам
- •2.2 Классификация по видам отказов
- •3. Показатели надёжности технических объектов
- •3.1 Общая характеристика показателей надёжности
- •3.2 Показатели надёжности технических объектов по свойству безотказности
- •Показатели надёжности по свойству безотказности
- •5. Показатели надёжности по свойству долговечности
- •4. Показатели надёжности по свойству ремонтопригодности
- •6. Показатели надёжности по свойству сохраняемости
- •6. Комплексные показатели надёжности
- •7. Периоды жизненного цикла изделия
- •Основные законы распределения случайных величин
- •Расчёт надёжности технических объектов
- •Расчёт показателей надёжности невосстанавливаемых резервированных систем
- •9.1 Расчёт показателей надёжности при последовательном соединении элементов в схеме
- •9.4 Сложные расчётные схемы надёжности
- •Оценка показателей надёжности восстанавливаемых нерезервированных систем
- •10.1 Потоки отказов и восстановлений работоспособности систем
- •10.2. Марковский случайный процесс
- •10.3 Типовые графы состояния функционирования системы
- •12.1 Особенности надёжности систем безопасности
- •12.2 Особенности функционирования систем безопасности. Структурно-функциональная надёжность
- •12.3 Общий подход к оценке параметро-точностной надёжности
- •12.4 Оценка эксплуатационно-прочностной составляющей надёжности
- •Профилактическое обслуживание
- •13.1 Регламентное профобслуживание
- •14.2 Выбор номенклатуры используемых показателей надёжности
- •14.3 Критичность отказов
10.3 Типовые графы состояния функционирования системы
Рассмотрим возможные виды графов на примере автоматической системы экологического мониторинга, состоящую из трёх элементов (модулей, подсистем): поста контроля ПК параметров окружающей среды; канала связи КС, центральной ЭВМ. Схема системы АСКОС представлена на рис. 27.
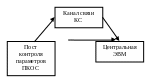
Рисунок 27 – Структура АСКОС
Восстанавливаемая, нерезервированная система. Отказ одного из элементов приводит к отказу всей системы экологического мониторинга. Изобразим функционирование данной системы с помощью теории графов (рис. 28):
![]() –
состояние безотказной работы АСКОС.
–
состояние безотказной работы АСКОС.
– состояние поста контроля после отказа;
– состояние канала связи после отказа;
– состояние центральной ЭВМ после отказа;
Система из состояния
переходит в состояние
с некоторым параметром
![]() (интенсивность
отказов), а из
в
параметром
(интенсивность
отказов), а из
в
параметром
![]() и в другие состояния.
и в другие состояния.

Рисунок 28 – Размеченный граф состояния системы
– интенсивность отказов;
![]() –
интенсивность восстановления.
–
интенсивность восстановления.
Граф гибели невосстанавливаемой системы показан на рисунке 29.

Рисунок 29 – Схема графа гибели
Системы из работоспособного состояния переходит в неработоспособное состояние при последовательном отказе элементов (рис. 30).
Граф гибели и размножения системы
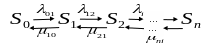
Рисунок 30 – Схема графа гибели и размножения
![]() –
состояние полного отказа, отказал
основной и все резервные элементы;
–
состояние полного отказа, отказал
основной и все резервные элементы;
– безотказное состояние;
– отказал основной элемент, а 1-ый резервный работает;
– отказал основной и 1-ый резервный, а работает 2-ой элемент.
Графы гибели описывают состояния резервированных, невосстанавливаемых систем.
Графы гибели и размножения описывают состояния резервированных восстанавливаемых систем.
Циклический граф
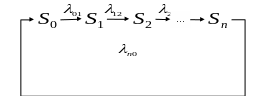
Рисунок 31 – Схема циклического графа
Через n шагов система переходит из одного состояния в другое. Она может прийти в начальное состояние , или в состояние функционирования после ремонта и т.д.
Выводы:
Пошаговый процесс
Состояние системы дискретно.
Время перехода системы из одного состояния в другое распределено экспоненциально.
Приведённые графы, при допущении, что поток событий — Пуассоновский, и время безотказной работы, а также время восстановления описаны экспоненциальным законом — это Марковские процессы.
Лекция 11
МАТЕМАТИЧЕСКИЙ АППАРАТ ГРАФОВ СОСТОЯНИЯ СИСТЕМ
Для примера принимаем граф (рис.32) восстанавливаемой нерезервируемой системы экологического мониторинга СЭМ. В этом случае оцениваются стандартные показатели надёжности: вероятность безотказной работы , коэффициент готовности , либо коэффициент оперативной готовности.

Рисунок 32 – Графическое представление
Вероятность нахождения системы в данном состоянии описывается Марковской моделью по схеме:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Вероятность изменения этого состояния
за малый промежуток времени
![]() описывается дифференциальным уравнением
вида:
описывается дифференциальным уравнением
вида:
![]() ,
,
где
![]() –
выражения состояний.
–
выражения состояний.
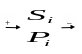
Вероятность
состояния элементов
![]() описывается системой аналогичных
дифференциальных уравнений:
описывается системой аналогичных
дифференциальных уравнений:
![]()
![]()
Для решения этой системы необходимо
знать значения интенсивностей отказов
![]() и восстановлений
и восстановлений
![]() ,
которые определяются опытным путём.
,
которые определяются опытным путём.
Если же система функционирует
продолжительное время (![]() ),
тогда она принимает вид:
),
тогда она принимает вид:
![]()
![]() .
.
Это система дифференциальных уравнений Колмогорова для графа состояний последовательных элементов. Она трансформируется в систему простых алгебраических уравнений:
![]()
![]()
Решение этой системы достигается путём
нормирования
![]() .
Тогда можно записать:
.
Тогда можно записать:
![]()
Решив систему алгебраических уравнений,
определяем
![]() ,
которое является коэффициентом готовности
:
,
которое является коэффициентом готовности
:
![]() — это есть уравнение надёжности
восстанавливаемых нерезервированных
систем в стационарном режиме.
— это есть уравнение надёжности
восстанавливаемых нерезервированных
систем в стационарном режиме.
Восстановление — есть рациональный
путь, как и резервирование, повышения
надёжности (
)
системы,
![]() .
.
Определив , можно найти коэффициент простоя . Уменьшая время простоя, увеличиваем .
Для невосстанавливаемых резервируемых систем имеются нижеследующие расчётные выражения ПН.
1. Для ненагруженной системы, вероятность безотказной работы резервированной системы
![]() ,
при
,
при
![]() ,
,
где
![]() —
среднее время безотказной работы
резервированной системы;
—
среднее время безотказной работы
резервированной системы;
– интенсивность отказов нерезервированной системы;
– кратность резервирования;
– число резервных элментов.
2. Для нагруженного резервирования:
![]() при
при
![]() ;
;
![]() .
.
3. Для системы с облегченным резервом:
![]() при
при
![]() ,
,
где – коэффициент, который показывает насколько резервный элемент разгружен по отношению к основному,
![]() .
.
Лекция 12
НАДЁЖНОСТЬ СИСТЕМЫ БЕЗОПАСНОСТИ
